Capping it all off

The Times Higher Education Supplement has a nice book review of a new text So thats how it all fits together by the celebrated mathematician John B. Conway. The book is designed for a "capstone" course at the end of a mathematics undergraduate degree. I thought the following introductory paragraph was helpful, and just as relevant to physics undergraduate education (at least in Australia):

 the increasing modularisation of university curricula has meant that the connections between different areas of mathematics are not always made apparent. Indeed, for many students who attended schools in England, their pre-university experience of mathematics is that it is presented as a range of topics to be mastered for assessment, and which can then be completely forgotten as the learner moves on to the next module. Undergraduates today often express surprise when they discover that a topic covered earlier in the curriculum is required elsewhere later. This attitude is profoundly depressing: do students really think that we are encouraging them to put enormous effort into learning things that are going to be of no future value?

The review also recommends several other texts for Capstone courses. I would be interesting in any recommendations for physics courses.

iPoverty

The New York Times has a nice article by Thomas Friedman, The Last Person about the Indian Institute for Technology in Rajasthan developing an extremely cheap tablet computer that is affordable [with some government subsidy] to the extremely poor.

Teaching scientific research methods

How does someone learn to do good research? Most scientists might claim it is by osmosis and experience. Social scientists tend to make graduate students take formal courses in "research methods". In contrast, natural scientists seem quite skeptical to such approaches.

Michael Marder has a new book out Research Methods for Science. It looks quite worthwhile because of the mix of background, hands on exercises, practical advice, statistics, .... It is based on a course he has co-taught to undergraduate science majors for a number of years at UTexas.

I welcome comments, particularly from people who have taught or taken such courses.

Careers should be driven by scientific reality not metrics

More and Different by Phil Anderson is stimulating and challenging holiday reading. Here is a paragraph from an essay, "Reflections on Twentieth Century Physics," which considers how from the 1950s to the end of the century:

There was a very sharp change in the nature of a research career. The "promising" young scientists publication rate grew by factors of five to ten; the number of applications a young researcher might make for post-doctoral work or an entry-level position rose from two or three to 50. Senior scientists were overwhelmed with receiving and sending reams of letters of recommendation, which thereupon became meaningless. The numbers of meetings .. grew by factors of ten or more... Most publications became tactical in this game of jockeying one's way to the top; publications in certain prestige journals were seen as essential entry tickets or score counters rather than as serious means of communication. Great numbers of these publications were about simulations of dubious realism or relevance. Essentially, in the early part of the post-war period the career was science-driven, motivated mostly by absorption with the great enterprise of discovery, and by genuine curiosity as to how nature operates. But the last decade of the century far too many, especially of the young people, were seeing science as a competitive interpersonal game, in which the winner was not the one who was objectively right as the the nature of scientific reality but the one who was successful at getting grants, publishing in PRL, and being noticed in the news pages of Nature, Science, or Physics Today.

More and Different, page 100.

I consider this is a painfully accurate description of the current reality. It is amazing to see how few papers [one or two per year] the leaders published back in the 50s and 60s.

Is there anyway out of this undesirable situation? We can't turn back the clock. However, we can all [both junior and senior scientists] exercise some critical judgement and self control and not be completely conformed to the system and our colleagues.
Keep the science at the forefront of our minds and pre-occupations, don't jump on the latest band-wagon or become obsessed with the latest "metric" of productivity.

Photo is Anderson and Richards looking at apparatus for experiments on superfluid 4He at Bell labs (in the 1960s) taken from the AIP archives. 

What is a metal?

How does one distinguish a metal from an insulator? One signature might be the presence of a charge gap at the chemical potential.
Is there a broken symmetry associated with a metal-insulator phase transition?

A key concept emphasized by Anderson is that distinct phases of matter are associated with the rigidity of their order parameter. For example, for a superconductor the superfluid density is associated with the phase stiffness of the ground state wave function.

It turns out that the Drude weight and the charge compressibility are both zero in a Mott insulator and non-zero in a metal. This is discussed in an interesting article by Imada. 

Aside: Imada's paper assumes the metal-insulator transition is continuous (i.e. not first-order) and derives scaling relations for the transition. This assumption may not be valid. At least, in dynamical mean-field theory the Mott transition at half filling is first order.

Kohn (and later Thouless) emphasized that for a metal one could calculate the Drude weight from the size and twist dependence of the ground state energy in the presence of twisted boundary conditions.

Imada considered a system at finite temperature and considered twisted boundary conditions in the imaginary time direction [anti-periodicity for fermions is required by the Kubo-Martin-Schwinger condition] showed that the charge compressibility determines the twist dependence.

I would be interested to see how the Drude weight and charge compressibility vary as one increases the temperature through the Fermi liquid - bad metal crossover.

Dialectic model building

Phil Anderson makes the following interesting comment [in the context of Cooper's treatment of the "pairing" problem] about model building in research.

Actually, in almost every case where I have been really successful it has been by dint of discarding almost all of the apparently relevant features of reality in order to create a “model” which has the two almost incompatible features: 

(1) enough simplicity to be solvable, or at least understandable; 

(2) enough complexity left to be interesting, in the sense that the remaining complexity actually contains some essential features which mimic the actual behavior of the real world, preferably in one of its as yet unexplained aspects. 

I said dangerous, and the sense in which this is true is that one is laying a trap for the majority of one’s colleagues, who are too literal-minded to understand either the necessity or the reality of the model-building process. A really well-built model can often stand a great deal of weight if used judiciously, but it can never hold up against being taken completely literally. 

P.W. Anderson, "BCS" and Me, More and Different, page 38.

I would argue that this approach has largely been abandoned in theoretical chemistry due to the dominance of computational chemistry.

A signature of a "two fluid" picture for a strongly correlated electron system

This post connects two seemingly disparate research topics of interest to me: optical properties of organic molecules and low energy excitations of strongly correlated electron materials. The connecting concept is that of an isosbestic point.

The figure below shows the absorption spectrum of an organic dye  for a range of pH values. Note that there is a wavelength (around 500 nm) at which all the spectra appear to cross. This is called the isosbestic point. Varying the pH varies the relative concentration of two forms of the dye molecule. Each form has a characteristic absorption peak (centred at lambda_1 and lambda_2 in the figure). The isosbestic point occurs at the wavelength at which the absorption due to each of the molecular forms has the same intensity. Hence, at this wavelength varying the relative concentration does not change the absorption intensity.

So what does this have to do with strongly correlated electron materials?
In 1997 Dieter Vollhardt published a PRL, Characteristic Crossing Points in Specific Heat Curves of Correlated Systems which pointed out that in liquid 3He, some heavy fermion materials, and the Hubbard model (solved by dynamical mean-field theory (DMFT)) there was a temperature at which the specific heat curves for different pressures (or Hubbard U or magnetic field) all crossed. Below is shown the data for liquid 3He. The crossing temperature is approximately that at which Fermi liquid theory breaks down.

Below are the curves for the Hubbard model.

This is not an artefact of DMFT since later Chandra, Kollar, and Vollhardt showed it is also present for the exact solution of the one-dimensional model.

I find this quite amazing!

Vollhardt made no mention of isosbestic points which I think would have been well known to many chemists. But, in 2007 there is Isosbestic Points in the Spectral Function of Correlated Electrons by Martin Eckstein, Marcus Kollar and Dieter Vollhardt.
It contains a nice discussion of the essential physics, including the connection to the spectra of dye molecules.
The paper contains the figure below of the spectral density for a Hubbard model (calculated with DMFT). The horizontal scale is frequency (omega) and the dashed curve is the non-interacting density of states.

So what does this all mean?

The key idea is one of "two fluids" i.e., that as one varies the relevant parameter (pressure, magnetic field or Hubbard U) all one is doing is varying the relative concentration of the two fluids. A sum rule requires one fluid must be converted into another. In the case of the Hubbard model the total number of electrons (area under A(omega)) is conserved. As one increases U one decreases the spectral weight in the Fermi liquid component (centred at omega=0) and increases the weight of the Hubbard bands (centred at omega=+-U/2).

One view from the trenches

The Heckler is a column in the Sydney Morning Herald where "Readers are invited to send 450 words about what makes their blood boil."
This week Nick Coleman had a piece "You could do this or go fishing" about the process for applying for research grants in Australia.

Observing the geometric phase in magnetoresistance II

Previously I posted how one could see a signature of Berry's geometric phase in Shubnikov de Haas experiments on graphene. Similar experiments and analysis of data for topological insulators produces ambiguous results, as discussed in this recent PRB by Taskin and Ando. In particular, the Berry phase gamma can be extracted from a "Landau level fan diagram" where one plots the inverse of the magnetic field B vs. the Landau level index N. Taskin and Ando claim that in the topological insulator the dispersion relation E(k) is non-linear and as a result

1. the fan diagram is non-linear

2. the Berry phase gamma deviates from pi and is a function of B

I am confused by 2. I would have thought that topology would require gamma to be only be pi or 0. This could be checked by looking at the eigenfunctions for the non-linear dispersion. Am I missing something?

The above claims are based on eqn. 8 in the paper. It is derived from the generalised Onsager condition which is a semi-classical condition relating the area of the quantised cyclotron orbit to Landau level index N.

I welcome clarifications.

More and Different

I have just started reading Phil Anderson's new book, More and Different: notes from a thoughtful curmudgeon. It is a collection of essays on wide ranging subjects: personal reminiscences, history, philosophy, sociology, science wars, ....
Some of these have been published before but many have not.

The history is fascinating and the science stimulating. I highly recommend the book and will hopefully post some highlights.

Last night I read the personal reminiscence "BCS and me" which gave me an even greater appreciation of just how tortuous the road to the theory was, how brilliant the solution was, and how it still left some important questions to be answered.

Strongly correlated electron systems in high magnetic fields II

When and how can a large magnetic field change the ground state of a strongly correlated electron metal?

An earlier post considered this question.

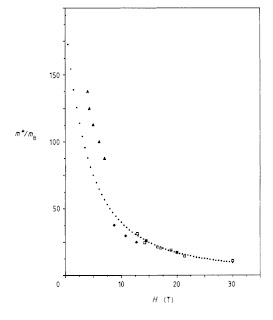
To me, one of the most striking cases is that of heavy fermion metals in high magnetic fields. From quantum magnetic oscillations [e.g., SdH and dHvA] one can measure the effective mass of the Fermi liquid quasi-particles. The figure below shows how in CeB6 the effective mass decreases significantly with increasing magnetic field. Hence, the field destroys the heavy fermion behaviour.

What is the physics behind this dramatic effect?
The heavy fermion character arises from the formation of Kondo singlets between the localised spins and the conduction electrons. However, an external magnetic field breaks these singlets, reducing the heavy fermion character. The Kondo lattice temperature [coherence temperature] sets the relevant magnetic field scale  and is well described by a slave boson theory of Wasserman, Springford, and Hewson [see eqn. 17 for m*(H)]. It also contains the above figure.

A more sophisticated treatment [connecting to recent NRG (Numerical Renormalisation Group) treatments of the single impurity Anderson model] of the case of YbRh2Si2 has recently been discussed by Zwicknagl. I am not clear on why she (and Hewson!) do not reference this earlier slave boson theory in their latest work.

The ultimate purpose of your teaching

There is an excellent New York Times online article What is College For? by Gary Gutting.
Here are just a few quotes to stimulate you to read the whole article.

the university curriculum leaves students disengaged from the material they are supposed to be learning.  They see most of their courses as intrinsically “boring,” of value only if they provide training relevant to future employment or if the teacher has a pleasing (amusing, exciting, “relevant”) way of presenting the material. As a result, students spend only as much time as they need to get what they see as acceptable grades (on average, about 12 to 14 hour a week for all courses combined).  Professors have ceased to expect genuine engagement from students and often give good grades (B or better) to work that is at best minimally adequate. ....

the raison d’être of a college is to nourish a world of intellectual culture; that is, a world of ideas, dedicated to what we can know scientifically, understand humanistically, or express artistically. 
Teachers need to see themselves as, first of all, intellectuals, Students, in turn, need to recognize that their college education is above all a matter of opening themselves up to new dimensions of knowledge and understanding.  
 It is more a matter of students moving beyond their interests than of teachers fitting their subjects to interests that students already have.   Good teaching does not make a course’s subject more interesting; it gives the students more interests — and so makes them more interesting.

I thank my lovely wife for bringing the article to my attention.

Is Papers 2.1 an improvement?

I really love the program Papers for the Mac.
They just released version 2.1 and so I downloaded a trial version.
However, after a week I reverted back to my old version 1. I had trouble getting the "Match" and "Query" functions to work and so gave up.
I welcome alternative views and suggestions.

RG theory of turbulence

The renormalisation group and scaling has proven to be an extremely powerful technique in theoretical physics. It has even been succesfully  applied to turbulence. A paper by Yakhot and Orczag in the Journal of Scientific Computing (!) is widely cited.

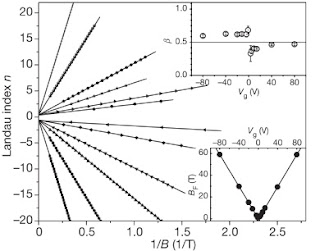
Observing the geometric phase in magnetoresistance I

The geometric (or Berry's) phase in quantum mechanics does have experimental manifestations in macroscopic materials. For example it can be seen in the phase of Shubnikov de Haas oscillations. The graph below is based on experimental data for graphene, taken from a 2005 Nature paper. In this "fan diagram" the Landau level index is plotted versus 1/B [the magnetic field at which a peak in the resistance occurs]. The y-axis) intercept (shown in the upper right inset as a function of gate voltage) is related to the Berry phase, beta. For a linear Dirac spectrum, beta=1/2 and for a quadratic spectrum, beta=0.

Similar experiments and analysis of data for topological insulators produces ambiguous results, which I will discuss in a forthcoming post about this recent PRB.

The Nernst effect in strongly correlated electron materials

The Nernst effect is a thermal conduction analogue of the Hall effect for electrical conductivity, i.e., it measures the transverse electrical current induced by a longitudinal thermal current in the presence of a magnetic field perpendicular to both currents.
It was considered an obscure (and very small) effect in elemental metals. However, the past 15 years it has become a powerful probe of strongly correlated metals, initially because of its sensitivity to superconducting fluctuations, as discussed by Ong.

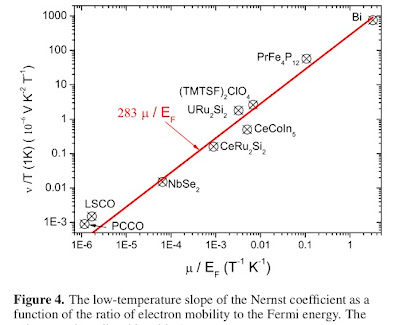
A nice helpful review is The Nernst Effect and the Boundaries of the Fermi Liquid Picture by Kamran Behnia.

He argues that the magnitude of the Nernst signal at low temperatures for a wide range of materials is proportional to the ratio of the charge carrier mobility to the Fermi energy. This is supported by the Figure below. Note the logarithmic scales.

A few notes.

1. The simple Fermi liquid expression [equation (8)] gives the Nernst signal as proportional to the energy derivative of the scattering time. For a Fermi liquid form of the scattering rate, the energy dependence is quadratic, and the signal will vanish. Essentially Behnia's replacement of the the energy derivative by the ratio of the scattering time and the Fermi energy means he is assuming that the scattering has a marginal Fermi liquid form. This is worth considering in more detail.

2. As the temperature increases there should be a crossover from a Fermi liquid with coherent quasi-particles with well-defined wavevectors to a "bad metal" with incoherent excitations. How this is manifested in the Nernst signal is an outstanding question.

3. A PRB by Kontani has given a general expression for the Nernst coefficient in a Fermi liquid including vertex corrections. A detailed analysis (within the framework of FLEX) claims that vertex corrections are important and due to antiferromagnetic fluctuations a large Nernst signal is possible in the pseudogap phase. [See Section 5.2 of this review].

What is the origin of magnetoresistance in silver chalcogenides?

Silver chalcogenides (e.g., Ag2Te) with slightly altered stoichiometry exhibit an unusual magnetoresistance. It is large and linear in field for magnetic fields up to about 6 tesla and temperatures between 5 and 300 K. [See this 1997 Nature paper].
Several possible physical origins of the magnetoresistance have been proposed.

1. A PRL earlier this year proposes is the material is a topological insulator with gapless surface states described by a highly anisotropic Dirac cone.

2. In 1998 Abrikosov proposed the materials are gapless semiconductors with a linear spectrum, doped to a small carrier concentration, and that only one Landau level contributes to the conductivity.

3. Parish and Littlewood's proposal that the key physics is that of a strongly spatially inhomogeneous semiconductor which can be described by a random resistor network.

4. I also note that a band structure which produces a non-zero Berry curvature can produce a linear magnetoresistance, according to p. 1984 of this Rev. Mod. Phys. [However, I suspect this is a very small effect].

The challenge is to come up with experimental signatures which can distinguish between the four different theoretical proposals.

From every angle

I am enjoying re-reading the book 5 Minds for the Future by Howard Gardner. The 5 minds are Disciplined, Synthetic, Creative, Respectful, and Ethical.

With regard to all of the first three he puts emphasis on the importance of considering the same topic from several angles and perspectives. In particular, creative needs to occur within a context of mastering earlier work.

I wonder how might this does and might happen in condensed matter theory?

Phenomenological vs. microscopic.
Strong coupling vs. weak coupling treatments.
Numerical vs. variational wave functions vs. field theories vs. renormalisation group.
A "chemical" approach concerned with specific details vs. a "physics" approach which neglects many details.

Other ideas?

I actually wonder whether we actually do this more often and better than some disciplines.   But that perception may be based on ignorance and hubris!

Seeking a unified theory for unconventional superconductors II

Phil Anderson has written an interesting comment on my earlier post on this subject. His comment might be read in conjunction with two earlier posts that are revelant.

Glueing together a theory is relevant to his comment about whether the pairing interaction is instantaneous.

Overdoped cuprates are an anisotropic marginal Fermi liquid is relevant to his comment about the Anderson-Casey theory of non-Fermi liquid effects.

I welcome further comments.

Deconstructing sodium cobaltate

Sodium cobaltate (NaxCoO2) is a strongly correlated electron material which achieved a lot of attention before the mass migration to the new iron pnictide superconductors following their discovery around 2008.
Some of the interest was motivated by the large thermopower, spin frustration associated with the underlying triangular lattice, and superconductivity from water!

Jaime Merino, Ben Powell, and I wrote several papers on the subject. At the cake meeting today we reviewed two papers which focused on the doping x=0.5.

Electronic and magnetic properties of the ionic Hubbard model on the striped triangular lattice at 3/4 filling

Ionic Hubbard model on a triangular lattice for Na0.5CoO2, Rb0.5CoO2, and K0.5CoO2: Mean-field slave boson theory
The latter features some really cool movies.

Here are some of the outstanding questions raised by the strange ground state of the x=0.5 material. It appears to be an insulator, with a small amount of charge order, a large magnetic moment which antiferromagnetically orders, and very small Fermi surface which produces quantum oscillations.
All these properties cannot be described by the strong coupling ground state [an antiferromagnetic insulator with charge order] shown below.

What is the ground state of the ionic Hubbard model on the triangular lattice at 3/4 filling for small Delta/t where Delta=measure of ionicity between the two sublattices?
Is it a covalent insulator? Does such a state have experimental signatures which are distinct from a charge ordered insulator?

How can an "insulating" state co-exist with a very small Fermi surface?

A simple concrete proposal to improve the quality of Australian undergraduate education

There is an opinion piece Up-end attendance rules for tutorial and lectures by Peter Van Onselen in the Higher Education Section of today's Australian newspaper. He is a Professor of Political Science at U. of Western Australia and a contributing editor to The Australian. He says that Arts/Humanities courses follow the "tried and true" format of two lectures and one tutorial per week. The former are optional and typically attract less than 50 per cent attendance. Tutorials are compulsory, are over-crowded, and diluted by students who have not done the assigned reading. He argues that the quality of education could be improved, without any additional costs, by making the lectures compulsory and the tutorials optional.

I prefer my own proposals: Fail more students and set the pass rate at the lecture attendance rate.

Ph.D completion time as a statistical variable

Seth Olsen brought to my attention an article Examining the Relationships among Doctoral Completion Time, Gender, and Future Salary Prospects for Physical Scientists in the Journal of Chemical Education.

It is based on a survey of more than 3000 Ph.D graduates of physics and chemistry in the USA. It claims there is a correlation (for men but not women) between Ph.D completion time and future salary. It also debates whether completion time is a good measure of the scientific merit of the graduate (the shorter the better) and the quality of the program (the longer the better!).

I found I was rather skeptical of many of the claims, values, and assertions in the article. [I also wonder about the reliability of the statistical methodology but am not claiming I could do any better...]. Nevertheless, the article is worth reading because all of the issues it raises and the literature that it surveys.

I welcome any comments on the article.

Optimal doping corresponds to maximum entropy

What is so unique about the optimal doping at which the superconducting transition temperature is a maximum in the cuprates?

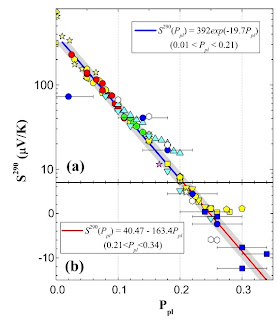
There is an interesting paper Unified electronic phase diagram for hold-doped high-Tc cuprates by Honma and Hor. It builds on their earlier work which argued the existence of a universal planar hole scale (P_pl), which can be characterised by the thermopower at T=290 K, denoted S^290. P_pl is independent of the nature of the dopant, the number of CuO2 plane layers per unit cell, the structure, and the sample quality. The figure below shows S^290 versus P_pl for a wide range of cuprates.

Note that the thermopower changes sign at a doping of P_pl ~ 0.25 which is comparable to that at which  Tc is a maximum [except for Sr doped La214]. 

What is the significance of this sign change of the thermopower?

For a simple Fermi liquid it would correspond to a change in the sign of the charge carriers, i.e., from electrons to holes.

Recently Peterson and Shastry interpreted this sign change in terms of the Kelvin formula for the thermopower, which gives the thermopower as -1/e times the derivative of the entropy with respect to the particle number. This can be related to the temperature dependence of the chemical potential via the Maxwell relation,

Here s=specific entropy, c_h=hole density, mu_h = chemical potential.

It is rather surprising that a transport property can be expressed in terms of a thermodynamic property.

Thus the change in sign of the thermopower means that the entropy is a maximum as a function of hole doping.

Indeed, a maximum in the entropy near optimal doping is was found for the t-J model via 

Finite temperature Lanczos calculations on small lattices of up to 20 sites and summarised in a 2000 review by Jaklic and Prelovsek.

The paper also considers a Kelvin type relation for the thermopower, but does not mention Kelvin, and shows how the maximum in the entropy vs. doping is associated with a change in sign of the thermopower.

[Peterson and Shastry do not mention this earlier work.]

A recent preprint by Garg, Shastry, Dave, and Philips, argue that the sign change reflects an underlying quantum critical point at optimal doping. However, I wonder about the extent that one can see a quantum critical effect on lattices as small as 20 sites. 

This is related to a 2009 PRB by Mark Jarrell and collaborators who calculated the temperature and doping dependence of the entropy using the cluster dynamical approximation. They found entropy was a maximum at optimal doping [~0.15-0.2]. They also don't mention the earlier work by Jaklic and Prelovsek.

A very strange metal

The linear chain compound Li0.9Mo6O17 exhibits a subtle competition between superconductivity, a "bad" metal, and a strange "insulating" phase. Recently large deviations from the Weidemann-Franz law were reported by Nigel Hussey's group.

The graph below shows the temperature dependence of the electrical resistance for current parallel to the chain direction. It has a "metallic" temperature dependence above about 30 K, and an "insulating" temperature dependence between the superconducting transition temperature around 1 K and 30 K. This is rather unusual and puzzling since one normally sees a direct transition from a metallic phase to a superconducting phase. Although there are other cases such as reported in this PRB [see Fig. 2 inset] for an organic charge transfer salt where a superconducting state occurs close to a charge ordered insulator [see also the Table in this PRL].

The data is taken from a Europhys. Lett. by Chen et al. which also reports a rather strange angular dependent magnetoresistance.

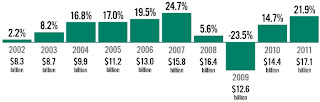
How much money does a "World class" university cost/need/want?

A lot!
This is a fact that I feel politicians who fund public universities just do not appreciate.
Here is a statistic that I find mind boggling.
Princeton University now has an endowment of $17.1 billion dollars!

Aside: the graph above shows how the endowment is now above pre-GFC levels.

What does that mean? Well, the university only has 5,000 undergraduates and 2,500 grad students. That means the average endowment per student is more than $2 million!
[This is the highest per student endowment in the world].
The university aims to spend the endowment at a rate of 4-5.75% on the annual operating budget. That means about $100 K per year is being contributed (indirectly) towards each students education. For reference annual tuition is about $36 K. Room and board are a further $12K per year.

How does the Mott insulating phase differ from the metallic phase near it?

For organic superconductors there is a first-order phase transition from a Mott insulator to  a superconductor with increasing pressure. This post concerns the relevant Hubbard model, that on an anisotropic triangular lattice at half filling, as discussed in this review.

With increasing U/t there is a first-order transition from a metal to an insulator.

This leads to a discontinuity in the double occupancy at the transition, illustrated in the sketch above.

The double occupancy D is shown below versus U/t for t'=0.8t. For reference D=0.25 for a half-filled system at U=0.

The figure is taken from a 2008 PRL by Ohashi et al.

D is calculated with Cluster Dynamical Mean-Field Theory (DMFT)

1.  A rough estimate of the  magnitude of D can be found from the Hellman-Feynman theorem D= dE_0/dU where E_0 is the ground state energy.
In the Mott phase this is dominated by the antiferromagnetic Heisenberg exchange J ~ 4t^2/U. Hence, D ~ (t/U)^2

2. The discontinuity in D at the metal-insulator transition  is relatively small, being about a 15 per cent change for T=0.1t, and less at higher temperatures. To me this suggests that in some sense the character of the metallic and insulating phases near the transition are not that different, just like a liquid and gas are hard to distinguish near the critical point.

3. These results are in contrast to Brinkmann-Rice theory [which ignores J] which gives D=0 in the Mott phase.

Covalent character of hydrogen bonds III

Following up on an earlier post about how indirect spin couplings in NMR (Nuclear Magnetic Resonance) may be a signature of the covalent character of hydrogen bonds I have been reading a range of papers on the subject. The Figure below shows how the calculated O-O nuclear coupling J correlates with the donor-acceptor distance [another example of an empirical correlation I have been highlighting].

The figure is taken from a 2000 JACS by Del Bene, Perera, and Bartlett.

One thing that is frustrating about reading most of these chemistry NMR papers is that they never explain the basic physics involved.

The Oxford Chemistry primer on NMR by Peter Hore has a useful section on Indirect coupling. He gives a nice simple argument explaining how [from 2nd order perturbation theory] the H-H coupling in the hydrogen molecule is roughly J ~ A^2/E  where A is the proton hyperfine interaction and E is the energy gap between the ground state and the lowest triplet state. This estimate gives J ~ 300 Hz, which is comparable to the actual value. Basically, when one flips one proton spin the A flips the electron spin, converting the ground state spin singlet into the excited triplet state.

The figure is taken by a nice webpage by Hans Reich

Deconstructing vertex corrections

Ultimately much of quantum many-body theory concerns calculating correlation functions which are measurable. For example, the conductivity can written as a current-current correlation function [Kubo formula]. The simplest approximation neglects vertex corrections and just calculates the "bubble" diagram consisting of the product of Green's functions.

What are vertex corrections? When do they matter? What sort of robust or general results are available about them?

Many people, including myself, often just ignore them. I fear this is partly motivated by difficulty rather good scientific criteria.

Below are a few things I am slowly learning, re-learning, and digesting.

Migdal showed that for the electron-phonon interaction the vertex corrections are small due to the smallness of the ratio of the electronic mass to the nuclear mass [alternatively the ratio of the speed of sound to the Fermi velocity].
But, Migdal's argument breaks down for an electron-magnon interaction.

Neglecting vertex corrections is equivalent to making the relaxation time approximation (RTA) when solving the Boltzmann equation. Then the quasi-particle lifetime equals the transport lifetime because one ignores dependence of the scattering rate on momentum transfer. Below is some helpful text from a review by Kontani:

 ....we have to take the Current Vertex Correction [CVC] into account correctly, which is totally dropped in the Relaxation Time Approximation [RTA]. In interacting electron systems, an excited electron induces other particle– hole excitations by collisions. The CVC represents the induced current due to these particle–hole excitations. The CVC is closely related to the momentum conservation law, which is mathematically described using the Ward identity [28–31]. In fact, Landau proved the existence of the CVC, which is called backflow in the phenomenological Fermi liquid theory, as a natural consequence of the conservation law [28]. The CVC can be significant in strongly correlated Fermi liquids owing to strong electron–electron scattering.

For specific types of interactions Ward identities allow one to relate the vertex function to derivatives of the self energy. Mahan's book (Section 8.1.3) discusses this in detail.

In the limit of infinite dimensions [in which Dynamical Mean-Field Theory (DMFT)] becomes exact, vertex corrections can be neglected.

In a recent PRB, Bergeron, Hankevych, Kyung, and Tremblay calculated the optical conductivity for the Hubbard model at the level of a two-particle self-consistent approach, including the constraint of the f-sum rule. They found that at "high" temperatures (T > 0.2t) vertex corrections did not matter much, but were significant at lower temperatures near a quantum critical point. 

Its all in the title?

An earlier post, Entitled to a reading, pointed out the value of carefully choosing engaging titles for your papers. Contrast the titles of the following two papers. The subject and conclusions of the papers are similar.
Benzene forms hydrogen bonds with water published in Science.

Low-J rotational spectra, internal rotation, and structures of several benzene-water dimers published in Journal of Chemical Physics.

Arunan brought this contrast to my attention.

Should you follow a textbook?

Yes. Closely.

This is the conclusion I have slowly come to over the years. Furthermore, the more junior the class the more closely you should follow a text.
Often I have struggled to find a text I thought suitable or have drawn on material from several books. This has meant giving out lecture notes.

It seems closely following a book is most effective if you can actually get students to read it! This appears to be a major goal of people who use methods such as Peer Instruction.

Having said all that you can expect student complaints. "You are just telling me what it is in the book". "There is too much reading". "Why are we paying you?" "Don't you have any ideas of your own!"

I welcome your thoughts. I would be curious to learn of systematic studies which showed whether student learning (rather than satisfaction and comfort) was actually enhanced by closely following a text.

Postdoc in theoretical chemical physics available at UQ

Seth Olsen and I have just advertised for a postdoc to work with us at UQ. The flavour of our interests and approach can be seen in posts on this blog under labels such as organic photonics, quantum chemistry, conical intersections, and Born-Oppenheimer approximation.

Competing phases are generic to strongly correlated electron systems

One might think that the Hubbard model on the square lattice with infinite U would be relatively boring. For example, a "simple" theory like Brinkman-Rice [or equivalently slave bosons] would predict that the ground state is a metal, except at half filling where it is a Mott insulator.

There is an interesting preprint Phases of the infinite U Hubbard model by Liu, Yao, Berg, and Kivelson. Here are a just a couple of the results concerning the ground state on a ladder, that I found interesting.

For 3/8 filling [3 electrons per 4 sites] they find the ground state is an insulator with a charge gap (0.24t) and plaquette bond order. The spin degrees of freedom are equivalent to those of a spin-3/2 antiferromagnetic Heisenberg model. I think this can be "understood" this by starting from the limit of weakly coupled placquettes with 3 electrons per plaquette.

For 1/4 filling the ground state is an insulator with a charge gap (~0.1t) and a small spin gap and "dimerisation". 

The authors argue these phases will also be stable for the actual isotropic square lattice.

It is fascinating to me that one can produce such rich and diverse broken symmetry states starting from such a relatively simple model which has no competing interactions in the Hamiltonian.

An earlier PRB by Yao, Tsai, and Kivelson, Myriad Phases of the checkerboard Hubbard model suggests competing phases are a generic feature of strongly interacting systems. 

Writing your first grant proposal

For most people this is one of the hardest and most tedious things to do. Some helpful thoughts are Writing the first proposal by John Wilkins [who mentored me through my first proposal!]. There is also a useful chapter in A Ph.D is not Enough, by Peter Feibelman.

Three basic questions you need to make sure your clearly and convincingly answer:

• Is the proposed project important?
• Is it feasible?
• Are you the best person to do the work?

Should cats be herded?

Everyone agrees that you need to herd cattle and sheep. But what about cats?
Cats are best enjoyed and fulfil their purpose if they are left alone and allowed to be what they are.

What is the relevance of this? It is sometimes claimed that academic researchers are like cats. They are fiercely independent and groups of them are very difficult to manage. Hence, books such as Herding Cats: Being advice to aspiring academic and research leaders by Geoff Garrett and Graeme Davies.

I became aware of the existence of the book because Geoff Garrett, who is now Queensland's Chief Scientist, gave the UQ Physics Colloquium on friday. I have not read the book. Afterwards a colleague expressed reservations about the ideas presented, saying, "this is relevant to engineers, not physicists!"

One idea that was presented was the importance of having a "Big Hairy Audacious Goal" which creates team spirit. Although laudable on some level, I am hard pressed to think of examples in science that have been fruitful or that I personally find inspiring. Maybe I am jaded but ones such as "nuclear fusion in our lifetime", "build a quantum computer", "discover a room temperature superconductor", "cheap organic solar cells to save the planet", or "lets make our university number one" just don't seem that achievable via highly managed research teams. 

Furthermore, it seems that most Nobel Prize discoveries did not result from such programs, but rather from curiousity driven research by "independent" research groups. One obvious exception are Nobel Prizes for discoveries in elementary particle physics.

What do you think?

Two persistent misconceptions about hydrogen bonding?

Misconception 1?
         "H-bonding interactions are dominated by electrostatics"
This is stated in Assessment of the Performance of DFT and DFT-D Methods for Describing Distance Dependence of Hydrogen-Bonded Interactions, one of the most downloaded recent papers in Journal of Chemical Theory and Computation.
Earlier posts discuss the importance of covalent interactions, particularly in shorter (stronger) Hydrogen bonds.


Misconception 2?

“One of the most fundamental, yet enigmatic, of all chemical processes is the transfer of protons in liquid water, which occurs via ultrafast quantum tunneling in the hydrogen bonded network”.

This is stated in a 2003 Science article and challenged by Dominic Marx in Proton Transfer 200 Years after von Grotthuss: Insights from Ab Initio Simulations

proton transfer has often readily been explained by taking recourse to the appealing concept of “proton tunneling”,27–29 which was begotten shortly after the birth of quantum mechanics. It is essentially based on a static view derived from symmetrical one-dimensional double-well potentials V(δ), such as the one shown on the left in Figure 3 [see below], thus completely omitting the possibility of a barrierless scenario, as sketched in the central panel of this figure. 

For a discussion of the origin [in terms of covalent interactions!] of these three different potentials, see my preprint.

Deconstructing the chemical potential of the cuprate superconductors

I have been reading through the nice review Finite temperature properties of doped antiferromagnets by Jaklic and Prelovsek from 2000. They summarise their studies of the t-J model by the Finite temperature Lanczos method.

At first sight the graph below of the temperature and doping dependence of the chemical potential does not look particularly interesting [at least to me]. However, they highlight its significance.

Here are a few points.

• In a simple Fermi liquid the chemical potential has a positive, quadratic and weak temperature dependence. This is only seen for doping c_h=x=0.3
• For a wide doping range [0.05 < c_h < 0.3] the temperature dependence is approximately linear. The slope changes sign for approximately optimal doping (c_h ~ 0.15).
• The weak temperature dependence for c_h ~ 0.15 means that optimal doping corresponds to maximum entropy!  [This can be deduced via the Maxwell relation below. Don't you love thermodynamics!]

• This relation is also related [approximately] to the thermopower via a relationship [equation 8.6], which is essentially a restatement of the Kelvin formula [discussed  by Peterson and Shastry].
• The latter means the thermopower should change sign around optimal doping, as is indeed observed [more on that later].
• The large entropy near optimal doping emerges from the interplay of the localised spins [from the remnants of the Mott insulator] and frustration of the antiferromagnetic spin interactions via doping.

I would be interested to see a similar calculation for the Hubbard model on the anisotropic triangular lattice at half filling to see how the chemical potential varies as a function of U/t as the Mott insulator is approached from within the metallic phase.

When the data is "too good to be true"

Remember Hendrik Schon! A decade ago he published a string of very impressive Nature and Science papers that eventually turned out to be "too good to be true". It seems a similar thing has been happening in the field of social psychology. The AP reports

 three graduate students grew suspicious of the data Stapel had supplied them without allowing them to participate in the actual research. When they ran statistical tests on it themselves they found it too perfect to be true and went to the university's dean with their suspicions.
In the future, the university plans to require raw data from studies to be preserved and made available to other researchers on request - a practice already common in most disciplines.

Nature News reports

The commission found that co-authors of Stapel's papers seem to have been unaware of the fraud, naively trusting in Stapel's reputation and fooled by elaborate preparations for tests that were never actually carried out..... Stapel and a colleague or student came up with a hypothesis, and then designed an experiment to test it. Stapel took responsibility for collecting data through what he said was a network of contacts at other institutions, and several weeks later produced a fictitious data file for his colleague to write up into a paper. On other occasions, Stapel received co-authorship after producing data he claimed to have collected previously that exactly matched the needs of a colleague working on a particular study.....
The data were also suspicious, the report says: effects were large; missing data and outliers were rare; and hypotheses were rarely refuted. Journals publishing Stapel's papers did not question the omission of details about where the data came from. 

This is part of a Nature News piece which has the misleading title "Report finds massive fraud at Dutch universities". A more responsible and accurate title would be "Report finds massive fraud by one Dutch professor of social psychology". In  the comments section several Dutch researchers rightly object to the title.

Chemistry driven by conical intersections

Nonadiabatic Quantum Chemistry is a nice Chemical Reviews article by David Yarkony.

It is quite succinct but covers a significant number of specific chemical systems where non-adiabatic effects [including conical intersections] are important and have been treated theoretically.

Here I just mention one example for which theory has failed so far, the vibrationally mediated photodissociation of NH3 (ammonia) to NH2 + H.
Experiments find that if the excited state contains a symmetric (asymmetric) N-H  stretch the dominant decay channel is to the NH2 ground state (excited state). Yarkony says that calculations [e.g. this one from Truhlar's group, which contains the figure below] have not yet captured this vibrational selectivity.

I thank Seth Olsen for bringing the article to my attention.

Should university be fun, fun, fun!

There is an interesting (and somewhat depressing) article in the New York Times Why Science Majors Change Their Minds (It's just so darn hard). It discusses how in the US there is a big push to have more STEM (Science, Technology, Engineering, and Mathematics) graduates but even if many start these degrees they do not finish.
One contributing factor is that these courses are graded harder than humanities courses.
The article also discusses initiatives, particularly in engineering courses, to make the courses more "fun" and "relevant", especially via projects.
I think this is all commendable and valuable. However, I have a sneaking discomfort that people [students, faculty, and administrators] just don't want to face the painful reality that engineering and science education does involve a certain amount of tedious hard work and that ultimately a lot of jobs (in any field) just aren't that exciting or satisfying.
Or am I just a grumpy old man?

I thank my wife for bringing the article to my attention.

A sign of something important

The Hall coefficient is a fundamental property of metals. In simple Fermi liquid metals it is temperature independent and inverse proportional to the charge carrier density. It has the same sign as the charge carriers (electrons or holes). A major triumph of the Bloch model of metals is that it could explain the sign of the Hall coefficient for simple metals in terms of their Fermi surface.

In contrast, the Hall coefficient of cuprate superconductors has a complex temperature and doping dependence which defies a simple description. Basic questions about the Hall coefficient are:

• What determines its sign?
• What is the origin of its temperature dependence?
• What is the relationship between it and the structure (or absence) of the Fermi surface?  

A 2006 PRB by Tsukada and Ono describes measurements of the Hall coefficient in the cuprate LSCO. The graph below shows the temperature dependence of the Hall coefficient for a range of dopings x of La2-xSrxCuO4 in the overdoped region. For reference, optimal doping is around x ~ 0.2, and for x larger than 0.3 there is no superconductivity. Note the sign change with increasing x.

The authors emphasize how this is a tricky measurement because one has to be careful that the current paths that are measured [to get both sigma_xx and sigma_xy needed for the Hall coefficient] really do lie in the plane of the layers and do not contain spurious contributions (see this earlier post about the challenge of electronic transport measurements in highly anisotropic materials).

The sign change may be an important signature of strong electronic correlations. I find it interesting (and surprising) that the observed sign change at x=0.3 is obtained in a high temperature series expansion of the high frequency Hall coefficient for the t-J model [in this 1994 PRL by Shastry, Shraiman, and Singh (SSS!)]. [An earlier post discusses Shastry's approach]. [Note: this calculation does not have a t' hopping term, which may be relevant. For example, it has a significant effect on the shape and  curvature of the Fermi surface and the proximity to van-Hove singularities. See below].

An alternative explanation of the sign change in terms of Mott physics was given by Stanescu and Phillips.

There may be a more mundane explanation in terms of changes in the Fermi surface associated with the proximity of the van Hove singularity in LSCO. Indeed ARPES experiments do find an electron-like Fermi surface for x~0.3. Furthermore, experiments on Tl2201 [which does not have a close van Hove singularity] do not see any hint of a decreasing Hall coefficient [or sign change] as one increases the doping on the overdoped side towards samples with Tc=0. [Higher dopings seem problematic for Tl2201].
Furthermore, one can quantitatively describe the temperature dependence of data for x=0.3  [including the sign change with temperature] if one uses a realistic Fermi surface and assumes that the impurity scattering rate is anisotropic over the Fermi surface. See this PRB; I thank Nigel Hussey for bringing it to my attention.

I thank Jure Kokalj for some helpful discussions.

Converging to the "right" answer

This week I had an interesting experience. I was doing a calculation and comparing my result to experiment. The comparison was poor, with a discrepancy of a factor of about two. This was disappointing, but then I decided that the theory was just too simple and one should not experiment anything better than qualitative agreement... I just had to accept this.
But then I found a mistake in my Mathematica code. I realised I had to check everything more carefully. .. One of my variables I had defined incorrectly... I redid the plot. The agreement of theory and experiment was excellent.

But, now there is a real danger. I could stop checking for errors. Afterall, given I already found a couple there may be another one which will lead to new discrepancies.
I will let you know if I find any. But, I have to confess the motivation to find errors is less than it was..

I wonder how often this happens in science.  I think I recall that there are some famous historical examples, e.g. that over years the value of the speed of light and the charge on the electron have drifted, but at any particular time peoples values have always been within a standard deviation of the latest measurements.

Just remember Feynman's warning: "The easiest person to fool is yourself."

The challenge of a simple measurement

Just because an experimentalist claims to have measured a specific physical quantity does not mean they actually have measured the desired quantity. Theorists need to be particularly wary at uncritically accepting data.

To most people, especially theorists, measuring the electrical resistivity of a metal sounds like an almost trivial measurement! Surely, you just stick a sample of the metal between the leads of an ohm-meter and read off the resistance!
The temperature dependence of the resistance can provide significant information about scattering of quasi-particles in the metal and any decent theory should be able to describe it. A famous case it the "linear in T" resistivity of optimally doped cuprate superconductors, a signature of non- Fermi liquid behaviour.

Most of the interesting strongly correlated metals (cuprates, organic charge transfer salts, iron pnictides, ....) have layered crystal structures leading to anisotropic electronic properties. These are sometimes referred to as quasi-two-dimensional metals.
Accurately, measuring the resistivity (and its temperature dependence) in the three different directions though is a highly non-trivial exercise. Basically, this is because you have to be sure that the current is going through the sample in the direction you think it is.

This is highlighted in a recent Nature Communications article from Nigel Hussey's group. They state:

 In a quasi-1D conductor, it is especially problematic to measure the smallest of the resistivity tensor components, because even a small admixture of either of the two larger orthogonal components can give rise to erroneous values and distort the intrinsic temperature dependence of the in-chain resistivity. In Li_0.9Mo₆O₁₇, reported room-temperature values for the in-chain (b axis) resistivity range from 400 μΩ cm²³ to more than 10 mΩ cm^34, 35.

Reported values for the ratio of the a to b axis resistivity vary from about 2 to 100!
This is a very large discrepancy!

I wrote this post because I thought I had come up with a fancy theoretical explanation of why in one paper the resistivity anisotropy ratio was only ~4, whereas band structure predicts a much larger value. However, when I surveyed the literature I discovered the result I was so proud of explaining is probably an artefact!