It was considered an obscure (and very small) effect in elemental metals. However, the past 15 years it has become a powerful probe of strongly correlated metals, initially because of its sensitivity to superconducting fluctuations, as discussed by Ong.
A nice helpful review is The Nernst Effect and the Boundaries of the Fermi Liquid Picture by Kamran Behnia.
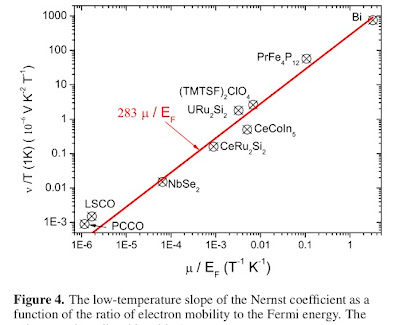
He argues that the magnitude of the Nernst signal at low temperatures for a wide range of materials is proportional to the ratio of the charge carrier mobility to the Fermi energy. This is supported by the Figure below. Note the logarithmic scales.
1. The simple Fermi liquid expression [equation (8)] gives the Nernst signal as proportional to the energy derivative of the scattering time. For a Fermi liquid form of the scattering rate, the energy dependence is quadratic, and the signal will vanish. Essentially Behnia's replacement of the the energy derivative by the ratio of the scattering time and the Fermi energy means he is assuming that the scattering has a marginal Fermi liquid form. This is worth considering in more detail.
2. As the temperature increases there should be a crossover from a Fermi liquid with coherent quasi-particles with well-defined wavevectors to a "bad metal" with incoherent excitations. How this is manifested in the Nernst signal is an outstanding question.
3. A PRB by Kontani has given a general expression for the Nernst coefficient in a Fermi liquid including vertex corrections. A detailed analysis (within the framework of FLEX) claims that vertex corrections are important and due to antiferromagnetic fluctuations a large Nernst signal is possible in the pseudogap phase. [See Section 5.2 of this review].
What do you think about the Nerts effect in a granular supercnductor?
ReplyDelete