Ben Powell alerted me to a stimulating post and comments about "Slow science" on the Quantum Pontiff blog.
It is worth thinking about. Here are a few random thoughts:
This gets back to a point I made in a few earlier "career advice" posts. Good reliable influential science is hard. Consequently, it is slow.
I think we all need to do more "slow" science. We would produce higher quality work AND enjoy ourselves more.
Don't blame the "system".
Focus on your "circle of influence" (e.g, what you CAN change: how you choose to spend your time, how you review grant proposals, and papers) rather than your "circle of concern" (i.e., what you care about but can't change, e.g., the way universities hire, promote, etc., funding agencies make decisions).
In spite of all the flaws of the "system" and the bean counters I think it is still clear that really significant work is rewarded.
I agree with John Preskill (and Clint Eastwood) each of us need to know our limitations. We are not all as brilliant as some of those who practice "slow" science, produce significant work, and prosper. We need to distinguish cause and effect. Trying to emulate Kitaev, Duncan Haldane, or John Cardy, Feynman, or Lars Onsager is not an option for most of us!
Tobias Osborne asks where does the pressure come from to keep producing papers ("correct but boring") and be in the limelight?
I think it is largely internal, i.e., psychological.
It is from habit, addiction, desire for affirmation,..
It is easier than the hard work of doing significant work.
Would you like to be freed up to spend 20% of your time doing "slow" science?
Here's how. It is "simple". Just say NO to 20% of the requests you get to collaborate, write conference papers, apply for grants, give seminars, review papers, review grants, sit on committees, go to conferences, .....
I doubt that the resulting 20% cut in "productivity" (hopefully, the 20% least valuable) will have much impact on how impressive your CV is.
Monday, June 29, 2009
Saturday, June 27, 2009
The naked truth versus self-deception
“With four parameters I can fit an elephant, and with five I can make him wiggle his trunk. ”John von Neumann (via Enrico Fermi and Freeman Dyson)
I believe that any significant physical effect/discovery should be able to be seen by the naked eye in the experimental (or computational) data and should not require curve fitting.
For a helpful discussion, see Dangerous Curves.
The first principle is that you must not fool yourself--and you are the easiest person to fool
Richard Feynman, Caltech 1974 Commencement address
Emergence matters
Reality is stratified and science is hierarchial: from physics to chemistry to biochemistry to biology to psychology. Generally, as one goes up the strata the complexity of the system under study increases and the relevant length and time scales become greater. At each strata or level of hierarchy, science seeks to illuminate what are the principles that describe the phenomena under study. Sometimes principles can be reduced to and understood in terms of principles from the strata below. For example, genetics can be understood in terms of molecular biology. Rules of chemical bonding can be understood in terms of quantum physics. However, it should be stressed that there are very few specific cases where phenomena at one strata have been predicted solely from a knowledge of the laws underlying strata below. In almost all cases, one observes (n.b., not deduces) phenomena at one level, develops concepts to understand them at that level, and then a posteriori tries to understand them in terms of the laws from the level below.
Perhaps is not appreciated enough just how hard it is to predict properties of quantum many-body systems. New phases of matter continue to be discovered: liquid crystals, quasicrystals, antiferromagnets, superfluids, …. Yet I am only aware of one case where a new state of matter was predicted and then discovered; that is Bose-Einstein condensates in dilute atomic gases were predicted.
Quantum chemistry involves using Schrodinger’s equation to calculate properties of molecules. It has many successes at calculating observed properties of small molecules. However, a measure of its limitations is the citation that one of the world leaders in the field, Fritz Schaefer, received for award of the Centenary Medal of the Royal Society of Chemistry in 1992: ``the first theoretical chemist successfully to challenge the accepted conclusions of a distinguished experimental group for a polyatomic molecule, namely methylene.”

In his classic More is Different paper, Phil Anderson emphasised that the success of methodological micro-reductionism does not imply a constructivist hypothesis: if we know the laws of one strata we can deduce the laws of the next strata above. Since making predictions from one strata to the next is so difficult, if not impossible, an a posteriori approach rather than an a priori approach is often necessary.
Perhaps is not appreciated enough just how hard it is to predict properties of quantum many-body systems. New phases of matter continue to be discovered: liquid crystals, quasicrystals, antiferromagnets, superfluids, …. Yet I am only aware of one case where a new state of matter was predicted and then discovered; that is Bose-Einstein condensates in dilute atomic gases were predicted.
Quantum chemistry involves using Schrodinger’s equation to calculate properties of molecules. It has many successes at calculating observed properties of small molecules. However, a measure of its limitations is the citation that one of the world leaders in the field, Fritz Schaefer, received for award of the Centenary Medal of the Royal Society of Chemistry in 1992: ``the first theoretical chemist successfully to challenge the accepted conclusions of a distinguished experimental group for a polyatomic molecule, namely methylene.”

In his classic More is Different paper, Phil Anderson emphasised that the success of methodological micro-reductionism does not imply a constructivist hypothesis: if we know the laws of one strata we can deduce the laws of the next strata above. Since making predictions from one strata to the next is so difficult, if not impossible, an a posteriori approach rather than an a priori approach is often necessary.
Friday, June 26, 2009
Closing the gaps in our understanding
As we struggle to understand the pseudogap state in the cuprate superconductors any successful theory must be able to describe at least qualitatively a few key features:
Furthermore, if it can, is there a "simple" physical picture of the underlying physics?
I believe that affirmative answers to both questions are given in a very nice preprint by Ferrero, Cornaglia, De Leo, Parcollet, Kotliar, and Georges.
Some of the results were published earlier in PRL, which contains the nice figure below of
the spectral function at the chemical potential at different doping away from half filling.

This work builds on the successes of Kotliar and Georges at developing Cluster Dynamical Mean-Field Theory (DMFT), rotationally invariant slave boson theory, and orbital-selective Mott transitions.
They divide momentum space into just two regions and consider the associated two-site DMFT. Symmetric and anti-symmetric combinations of the two sites correspond to the nodal and anti-nodal regions, respectively.
Formation of the pseudogap is associated with a Mott transition in the anti-symmetric orbital. The different behaviours of the two orbitals (momentum regions) is due to the formation of inter-site spin singlets. They compare the essential physics to that which occurs in the two-impurity Anderson model. In that case there is competition when formation of a singlet between the two impurities and two separate Kondo singlets between
each of the impurity spins and the itinerant electrons.
The calculations agree well with STM and ARPES experiments.
- the d-wave symmetry
- the existence of Fermi arcs which increase in length with doping
- well-defined quasi-particles near the nodes
- incoherent excitations near the anti-nodes
Furthermore, if it can, is there a "simple" physical picture of the underlying physics?
I believe that affirmative answers to both questions are given in a very nice preprint by Ferrero, Cornaglia, De Leo, Parcollet, Kotliar, and Georges.
Some of the results were published earlier in PRL, which contains the nice figure below of
the spectral function at the chemical potential at different doping away from half filling.

This work builds on the successes of Kotliar and Georges at developing Cluster Dynamical Mean-Field Theory (DMFT), rotationally invariant slave boson theory, and orbital-selective Mott transitions.
They divide momentum space into just two regions and consider the associated two-site DMFT. Symmetric and anti-symmetric combinations of the two sites correspond to the nodal and anti-nodal regions, respectively.
Formation of the pseudogap is associated with a Mott transition in the anti-symmetric orbital. The different behaviours of the two orbitals (momentum regions) is due to the formation of inter-site spin singlets. They compare the essential physics to that which occurs in the two-impurity Anderson model. In that case there is competition when formation of a singlet between the two impurities and two separate Kondo singlets between
each of the impurity spins and the itinerant electrons.
The calculations agree well with STM and ARPES experiments.
Thursday, June 25, 2009
Abolish conference proceedings!
I almost never take up an offer by conference organisers
to publish a paper in their proceedings. I think such
proceedings have passed their use by date because:
* They usually appear 6 to 18 months after the conference.
By then most of the papers have already been published elsewhere
* Almost all conference papers seem to be cut-and-paste versions
of papers that the authors have already published or about to
publish elsewhere.
* Most proceedings are published by mediocre journals.
* One of the main reasons some people publish in them is to pad their
publication lists and keep bean counters happy.
* The only conference papers I tend to read are review articles based on plenary talks by leading scientists. But, most of these I get off the arXiv.
Given all of the above I think conference proceedings are just a
waste of time for the organisers, referees, and authors.
We should all exercise more self-control and abstain.
to publish a paper in their proceedings. I think such
proceedings have passed their use by date because:
* They usually appear 6 to 18 months after the conference.
By then most of the papers have already been published elsewhere
* Almost all conference papers seem to be cut-and-paste versions
of papers that the authors have already published or about to
publish elsewhere.
* Most proceedings are published by mediocre journals.
* One of the main reasons some people publish in them is to pad their
publication lists and keep bean counters happy.
* The only conference papers I tend to read are review articles based on plenary talks by leading scientists. But, most of these I get off the arXiv.
Given all of the above I think conference proceedings are just a
waste of time for the organisers, referees, and authors.
We should all exercise more self-control and abstain.
Tuesday, June 23, 2009
What is reductionism?
In order to understand the role and implications of emergence it is helpful to define different forms of reductionism in science. It is also important to make a distinction between reductionism as a practice in science and reductionism as a philosophical outlook. As a method, reductionism has been extremely powerful. Examples of successes include the understanding obtained by reducing genetics to molecular biology, atomic spectra to quantum mechanics, and planetary motion to Newtonian mechanics. A reductionist approach gave a unifying description of a diverse range of phenomena, and elucidated "cause and effect", i.e., if one component or variable of the system is changed what is the resulting change in other components or properties. In terms of popular books, advocates of the primacy of reductionism include Steven Weinberg, Stephen Hawking, and Richard Dawkins. They also appear to presuppose that because reductionism is a fruitful strategy for certain scientific problems that these means that a philosophical reductionism must be universally valid.
The Oxford Companion to Philosophy considers three aspects of philosophical reductionism: ontological, methodological, and theory.
Ontological reductionism "refers to the belief that the whole of reality consists of a minimal number of entities." For example, humans are really just self-organising biochemical systems or that the world is just a collections of quarks, leptons, and gauge fields. This often appears to involve value judgements as to what is "real" and what is not.
Methodological reductionism claims that ``the best scientific strategy is always to attempt explanation in terms of ever more minute entities.’’ One can differentiate this methodology further in terms of micro-reductionism and macro-reductionism. The former focuses on explaining phenomena at one strata in terms of the next lowest level strata. For example, genetics can be understood in terms of DNA. Macro-reductionism goes much further, claiming to explain phenomena at one level in terms of phenomena at a much lower strata. Socio-biology is an example of macro-reductionism. Micro-reductionism has proven to be an extremely successful and fruitful strategy; it has led to a simplification of ideas and unification of knowledge. However, it is contentious whether it is always the best scientific strategy. Although macro-reductionism has prominent, articulate, and passionate advocates I am unable to think of any specific cases where it has actually been able to produce knowledge that has been accepted by a majority of scientists in the associated field.
Theory (or epistemological) reduction considers how one theory which replaces a prior one reduces to it in an appropriate limit. For example, Einstein’s theory of special relativity reduces to classical Newtonian mechanics in the limit of objects moving much less than the speed of light. Similarily, the equations of quantum physics reduce to those of classical mechanics in the limit of large objects. This was advocated by the ``Unity of science’’ movement in the 1930’s and the influential work by Nagel [The Structure of Science, (Harcourt, New York, 1961)] who claimed that reduced theories were just logical consequences of the reducing theory. Thomas Kuhn, considers that theory reduction is not possible because new theories often involve concepts and modes of explanation that are ``incommensurate’’ with prior theories. For example, although in appropriate mathematical limits quantum theory reduces to classical mechanics, they do not agree on whether on can ascribe a definite position and momentum to a single particle. A less radical view emphasizes the complexity and subtleties associated with theory reduction because it requires limiting procedures, coarse graining and approximations. [R. Batterman, The Devil in the Details. Asymptotic Reasoning in Explanation, Reduction, and Emergence (Oxford: Oxford University Press, 2002).]
The Oxford Companion to Philosophy considers three aspects of philosophical reductionism: ontological, methodological, and theory.
Ontological reductionism "refers to the belief that the whole of reality consists of a minimal number of entities." For example, humans are really just self-organising biochemical systems or that the world is just a collections of quarks, leptons, and gauge fields. This often appears to involve value judgements as to what is "real" and what is not.
Methodological reductionism claims that ``the best scientific strategy is always to attempt explanation in terms of ever more minute entities.’’ One can differentiate this methodology further in terms of micro-reductionism and macro-reductionism. The former focuses on explaining phenomena at one strata in terms of the next lowest level strata. For example, genetics can be understood in terms of DNA. Macro-reductionism goes much further, claiming to explain phenomena at one level in terms of phenomena at a much lower strata. Socio-biology is an example of macro-reductionism. Micro-reductionism has proven to be an extremely successful and fruitful strategy; it has led to a simplification of ideas and unification of knowledge. However, it is contentious whether it is always the best scientific strategy. Although macro-reductionism has prominent, articulate, and passionate advocates I am unable to think of any specific cases where it has actually been able to produce knowledge that has been accepted by a majority of scientists in the associated field.
Theory (or epistemological) reduction considers how one theory which replaces a prior one reduces to it in an appropriate limit. For example, Einstein’s theory of special relativity reduces to classical Newtonian mechanics in the limit of objects moving much less than the speed of light. Similarily, the equations of quantum physics reduce to those of classical mechanics in the limit of large objects. This was advocated by the ``Unity of science’’ movement in the 1930’s and the influential work by Nagel [The Structure of Science, (Harcourt, New York, 1961)] who claimed that reduced theories were just logical consequences of the reducing theory. Thomas Kuhn, considers that theory reduction is not possible because new theories often involve concepts and modes of explanation that are ``incommensurate’’ with prior theories. For example, although in appropriate mathematical limits quantum theory reduces to classical mechanics, they do not agree on whether on can ascribe a definite position and momentum to a single particle. A less radical view emphasizes the complexity and subtleties associated with theory reduction because it requires limiting procedures, coarse graining and approximations. [R. Batterman, The Devil in the Details. Asymptotic Reasoning in Explanation, Reduction, and Emergence (Oxford: Oxford University Press, 2002).]
Monday, June 22, 2009
Desperately seeking spin liquids
What is a spin liquid? There are several alternative definitions.
The definition that I think is the most illuminating, because it brings out their truely exotic nature, is the following. A spin liquid is a quantum state in which there is no long-range magnetic order and no breaking of spatial symmetries (rotation or translation).
One can write down many such states. A concrete example is the ground state of the one-dimensional antiferromagnetic Heisenberg model with nearest-neighbour interactions.
However, despite an exhaustive search since Anderson's 1987 RVB paper, it seems extremely difficult to find a physically realistic Hamiltonian in two dimensions which has such a ground state.
As far as I am aware we are still seeking a counter-example to the following conjecture:
Consider an spin-1/2 Heisenberg model on a two-dimensional lattice with short range antiferromagnetic exchange (both pairwise and ring exchange are allowed) interactions. The Hamiltonian is invariant under SU(2)xL, where L is a space group. Then the ground state spontaneously breaks at least one of the two symmetries SU(2) and L.
Or did I miss something?
The definition that I think is the most illuminating, because it brings out their truely exotic nature, is the following. A spin liquid is a quantum state in which there is no long-range magnetic order and no breaking of spatial symmetries (rotation or translation).
One can write down many such states. A concrete example is the ground state of the one-dimensional antiferromagnetic Heisenberg model with nearest-neighbour interactions.
However, despite an exhaustive search since Anderson's 1987 RVB paper, it seems extremely difficult to find a physically realistic Hamiltonian in two dimensions which has such a ground state.
As far as I am aware we are still seeking a counter-example to the following conjecture:
Consider an spin-1/2 Heisenberg model on a two-dimensional lattice with short range antiferromagnetic exchange (both pairwise and ring exchange are allowed) interactions. The Hamiltonian is invariant under SU(2)xL, where L is a space group. Then the ground state spontaneously breaks at least one of the two symmetries SU(2) and L.
Or did I miss something?
Saturday, June 20, 2009
The theory of everything
This is the provocative title of a very nice paper by Laughlin and Pines in PNAS back in 2000. They point out that in principle Schrodinger's equation from quantum mechanics and Coulomb's law of electrostatics is ‘The Theory of Everything’ since these equations determine all of chemistry and all the properties of all matter that we encounter everyday. Yet, due to limited computational resources even the most powerful supercomputer can only solve these equations and make predictions for systems containing at most ten particles. However, even if we had a supercomputer that could treat Avogadro's number (i.e., 10^23) of particles that would not help. Such a computer would require more atoms than there are in the universe.
First, doing the calculations would be just like doing an experiment. It would be a ‘black box’ that would give little insight into the origin of the phenomena. Morever, such calculations on finite systems cannot predict phenomena such as broken symmetry and the exact quantisation of quantities such as the quantum Hall resistance, the magnetic flux associated with a vortex in a type II superconductor, or the circulation associated with a vortex in superfluid Helium. If we ‘know the answer’, i.e., expect broken symmetry, then we can ‘jig’ the equations so we can get the answer out. But this is a posteriori not a priori reasoning.
Phenomena such as the quantisation of magnetic flux of vortices in type II superconductors present a problem for methodological reductionism. Even though Ginsburg-Landau theory is only approximate and does not require a detailed knowledge of the underlying quantum dynamics of the constituent atoms and electrons in a superconducting metal it predicts exactly the value of the magnetic flux. This is because of the principle of broken symmetry.
First, doing the calculations would be just like doing an experiment. It would be a ‘black box’ that would give little insight into the origin of the phenomena. Morever, such calculations on finite systems cannot predict phenomena such as broken symmetry and the exact quantisation of quantities such as the quantum Hall resistance, the magnetic flux associated with a vortex in a type II superconductor, or the circulation associated with a vortex in superfluid Helium. If we ‘know the answer’, i.e., expect broken symmetry, then we can ‘jig’ the equations so we can get the answer out. But this is a posteriori not a priori reasoning.
Phenomena such as the quantisation of magnetic flux of vortices in type II superconductors present a problem for methodological reductionism. Even though Ginsburg-Landau theory is only approximate and does not require a detailed knowledge of the underlying quantum dynamics of the constituent atoms and electrons in a superconducting metal it predicts exactly the value of the magnetic flux. This is because of the principle of broken symmetry.
Thursday, June 18, 2009
Keeping the focus
 "The main thing is to keep the main thing the main thing"
"The main thing is to keep the main thing the main thing"Lee Iacocca, former CEO of Chrysler, who in the 80's turned the company around.
[He is about to loose his pension ....]
Anyway, each year I have to do several staff appraisals. It is easy to get distracted by the onerous paperwork and lists of publications, grants, future plans...
Here are some questions I want to focus on this year.

- What did you enjoy the most about the past year?
- What did you enjoy the least about the past year?
- What specific scientific questions did your research answer in the last year?
- What specific scientific questions do you want your research to answer in the next year?
- The worst enemy of the excellent is the good. What should you say no to in the next year?
- How can I better help you reach your goals this year?
Tuesday, June 16, 2009
A universal (almost) phase diagram for iron pnictide superconductors
 A recent preprint from Ni, Thaler, Kracher, Yan, Budko, and Canfield (Ames Lab, Iowa State) reports the above phase diagram for members of the 122 family (based on the parent compound BaFe2As2). When doped with transition metals the antiferromagnetic transition is suppressed and superconductivity appears below the lower dome. Near the antiferromagnetic transition there is also a structural transition from a tetragonal to an orthorhombic crystal structure.
A recent preprint from Ni, Thaler, Kracher, Yan, Budko, and Canfield (Ames Lab, Iowa State) reports the above phase diagram for members of the 122 family (based on the parent compound BaFe2As2). When doped with transition metals the antiferromagnetic transition is suppressed and superconductivity appears below the lower dome. Near the antiferromagnetic transition there is also a structural transition from a tetragonal to an orthorhombic crystal structure.
Monday, June 15, 2009
Quantum dynamics of excited states of biomolecular chromophores
I am giving the Chemistry seminar at UQ this week. Here are the slides
Saturday, June 13, 2009
Emergent paradoxes
 A book I really like and strongly recommend is A Different Universe: Reinventing Physics from the Bottom Down by Bob Laughlin. He received the Nobel Prize in Physics in 1998 for the theoretical description of the fractional quantum Hall effect, and was a co-founder of I2CAM. Laughlin has highly original ways of looking at science and is a very gifted writer.
A book I really like and strongly recommend is A Different Universe: Reinventing Physics from the Bottom Down by Bob Laughlin. He received the Nobel Prize in Physics in 1998 for the theoretical description of the fractional quantum Hall effect, and was a co-founder of I2CAM. Laughlin has highly original ways of looking at science and is a very gifted writer.Laughlin is passionate advocate for emergent phenomena being the most interesting and challenging aspect of science.
Just to illustrate some of the insights.... Laughlin points out
that emergent phenomena can present significant paradoxes. Laughlin considers two paradoxes associated with the Integer Quantum Hall effect. First, there is “perfection due to imperfection”: the precision of the quantisation of the Hall resistance improves as the sample quality decreases, i.e., the number of impurities that scatter the electrons increases. Second, the Quantum Hall effect provides a very precise means to determine properties of elementary particles from measurements on macroscopic samples. It measures the fine structure constant, which is defined in terms of the properties of single electrons: the electronic charge, Planck’s constant, and the speed of light.
Friday, June 12, 2009
Organic superconductor information overload?
Here is a rough summary of a few things I think I learnt (or was reminded of) this week about superconducting organic charge transfer salts.
Please post corrections and clarifications. Where there is interest I will post more details...
A long-standing mystery in the Bechgaard salts has been the presence of rapid oscillations associated with an unexpected Fermi surface reconstruction. Could this be a many-body effect as in the cuprates?
(DMe-ET)2PF6 has superconductivity next to a charge ordered insulator.
Near the Mott transition critical point the low temperature NMR relaxation rate 1/T1 T should scale with |P-Pc|^delta, where delta =2 is the same critical exponent as for the conductivity.
This is because at half filling the number of localised spins is related to the number of doublons.
Kagawa et al., PRB 78, 184402 (2008) have a very elegant way of using NMR and the DM interaction to determine the staggered magnetisation (something is normally only observable via neutron scattering) above the Neel temperature.
The spin liquid material kappa-(ET)2(CN)3 has a specific heat which is linear in temperature at low temperatures. This is in distinct contrast to ET materials which have an antiferromagnetic
ground states. Combining the specific heat coefficient gamma with the low temperature susceptibility, would give a Sommerfeld-Wilson ratio of 1-2, characteristic of a ground state with gapless fermionic excitations, as proposed by P.A. Lee and collaborators.
I would think this would also mean that the dimensionless Korringa ratio should be unity.
The Bechgaard salts (based on the TMTSF molecule) have a spin-density wave insulating state with a relatively small magnetic moment. However, one should be cautious about claiming that Mott physics is not relevant to these materials since at lower chemical pressures there are Mott insulating, antiferromagnetic and spin Peierls states. (see the phase diagram below provided by Martin Dressel). Furthermore, even in the metallic state the Drude peak has extremely small
spectral weight and only exists below temperatures of about 10 K.

It is often claimed that in these materials the role of pressure is to increase the interchain hopping integral t_b and to reduce Fermi surface nesting. However, as far as I am aware there are no band structure calculations or direct experimental measurements to back this up. [Please correct me?]
Looking at how the critical field for the magnetic field induced spin-density wave (FISDW) varies with pressure may illuminate this, since the Lebed-Gorkov theory shows how the
critical field is related to tb', the hopping integral between
second-neighbour chains. Chaikin has a nice review on the FISDW's.
In the normal metallic state Stuart Brown and collaborators find that 1/(T_1 T) has a "Curie-Weiss" form 1/(T+theta) for a range of pressures (see his chapter in the book edited by Lebed). It is found that the parameter theta increases with pressure. Theta defines the temperature scale at which there is a crossover from Korringa (1/T1 linear in T) behaviour to T1 independent of T. Such a form is predicted naturally by the Moriya-Ueda antiferromagnetic
spin fluctuation theory near a quantum critical point in two dimensions. There, theta is the temperature scale over which the antiferromagnetic correlation length varies. In contrast, the resistivity does not appear to show any such crossover. It is dominated by a linear in T term, whose magnitude decreases with increasing pressure. Understanding this difference in the charge and spin response is an important question that needs to be resolved.
Please post corrections and clarifications. Where there is interest I will post more details...
A long-standing mystery in the Bechgaard salts has been the presence of rapid oscillations associated with an unexpected Fermi surface reconstruction. Could this be a many-body effect as in the cuprates?
(DMe-ET)2PF6 has superconductivity next to a charge ordered insulator.
Near the Mott transition critical point the low temperature NMR relaxation rate 1/T1 T should scale with |P-Pc|^delta, where delta =2 is the same critical exponent as for the conductivity.
This is because at half filling the number of localised spins is related to the number of doublons.
Kagawa et al., PRB 78, 184402 (2008) have a very elegant way of using NMR and the DM interaction to determine the staggered magnetisation (something is normally only observable via neutron scattering) above the Neel temperature.
The spin liquid material kappa-(ET)2(CN)3 has a specific heat which is linear in temperature at low temperatures. This is in distinct contrast to ET materials which have an antiferromagnetic
ground states. Combining the specific heat coefficient gamma with the low temperature susceptibility, would give a Sommerfeld-Wilson ratio of 1-2, characteristic of a ground state with gapless fermionic excitations, as proposed by P.A. Lee and collaborators.
I would think this would also mean that the dimensionless Korringa ratio should be unity.
The Bechgaard salts (based on the TMTSF molecule) have a spin-density wave insulating state with a relatively small magnetic moment. However, one should be cautious about claiming that Mott physics is not relevant to these materials since at lower chemical pressures there are Mott insulating, antiferromagnetic and spin Peierls states. (see the phase diagram below provided by Martin Dressel). Furthermore, even in the metallic state the Drude peak has extremely small
spectral weight and only exists below temperatures of about 10 K.

It is often claimed that in these materials the role of pressure is to increase the interchain hopping integral t_b and to reduce Fermi surface nesting. However, as far as I am aware there are no band structure calculations or direct experimental measurements to back this up. [Please correct me?]
Looking at how the critical field for the magnetic field induced spin-density wave (FISDW) varies with pressure may illuminate this, since the Lebed-Gorkov theory shows how the
critical field is related to tb', the hopping integral between
second-neighbour chains. Chaikin has a nice review on the FISDW's.
In the normal metallic state Stuart Brown and collaborators find that 1/(T_1 T) has a "Curie-Weiss" form 1/(T+theta) for a range of pressures (see his chapter in the book edited by Lebed). It is found that the parameter theta increases with pressure. Theta defines the temperature scale at which there is a crossover from Korringa (1/T1 linear in T) behaviour to T1 independent of T. Such a form is predicted naturally by the Moriya-Ueda antiferromagnetic
spin fluctuation theory near a quantum critical point in two dimensions. There, theta is the temperature scale over which the antiferromagnetic correlation length varies. In contrast, the resistivity does not appear to show any such crossover. It is dominated by a linear in T term, whose magnitude decreases with increasing pressure. Understanding this difference in the charge and spin response is an important question that needs to be resolved.
Thursday, June 11, 2009
Mind the gaps
Here is a rough summary of a few things I think I learnt this week. More to come later...
Please post corrections and clarifications.
A lot of attention in both STM and ARPES studies on the cuprates is being given to questions of particle-hole symmetry. This is because in a superconducting d-wave gap, the Bogoliubov quasi-particles have perfect particle-hole symmetry. In contrast, other possible nodal states such as the staggered flux phase (d-density wave, DDW) do not have this property.
The evidence from both STM and ARPES is that the physical origin of the gap near the nodes is quite different from the gap at the anti-nodes. They have different temperature and doping dependence. The consensus also seems to be that the gap near the nodes is from fluctuating superconductivity.
Some of the issues are nicely summarised in a Science Perspective by Andy Millis.
Electronic Raman Scattering (ERS) is a sensitive probe of the d-wave gap and pseudogap. The B1g polarisation ERS is dominated by quasi-particles near the anti-nodal part of the Brillouin zone. In contrast, the B2g polarisation response is dominated by the nodal part.
In the cuprates Tc tends to increase (decrease) with pressure in the underdoped (overdoped) region. Is this simply because pressure decreases correlations and so increasing pressure is equivalent to a small increase in doping?
Please post corrections and clarifications.
A lot of attention in both STM and ARPES studies on the cuprates is being given to questions of particle-hole symmetry. This is because in a superconducting d-wave gap, the Bogoliubov quasi-particles have perfect particle-hole symmetry. In contrast, other possible nodal states such as the staggered flux phase (d-density wave, DDW) do not have this property.

The evidence from both STM and ARPES is that the physical origin of the gap near the nodes is quite different from the gap at the anti-nodes. They have different temperature and doping dependence. The consensus also seems to be that the gap near the nodes is from fluctuating superconductivity.
Some of the issues are nicely summarised in a Science Perspective by Andy Millis.
Electronic Raman Scattering (ERS) is a sensitive probe of the d-wave gap and pseudogap. The B1g polarisation ERS is dominated by quasi-particles near the anti-nodal part of the Brillouin zone. In contrast, the B2g polarisation response is dominated by the nodal part.
In the cuprates Tc tends to increase (decrease) with pressure in the underdoped (overdoped) region. Is this simply because pressure decreases correlations and so increasing pressure is equivalent to a small increase in doping?
Wednesday, June 10, 2009
How bad can it get?
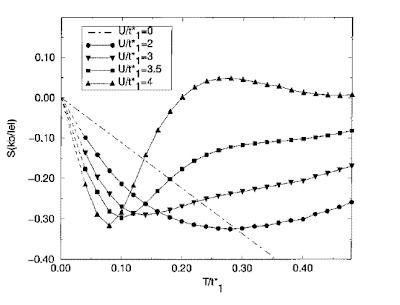
Hearing some talks about properties of the metallic state of the iron pnictide superconductors underscored to me that one sees certain common features in a wide range of strongly correlated electron materials. These properties are distinctly different from electronic properties of elemental metals. These unusual properties arise from the fact that a low energy scale emerges which defines a temperature scale T0 (often in the range 10-100 K) above which quasi-particles do not exist and we have a bad metal. Signatures of this crossover from a Fermi liquid at low temperature to a bad metal are:
All of the above features in the transport are captured by a dynamical mean-field theory (DMFT) treatment of a range of lattice Hamiltonians such as the Hubbard model and Anderson lattice model. These issues are discussed in more detail in a paper Jaime Merino and I wrote 10 years ago. The figure below illustrates how sensistive the thermopower is to the destruction of quasi-particles.
 A recent paper by Haule and Kotliar considered the coherence-incoherence crossover in the pnictides using LDA-DMFT.
A recent paper by Haule and Kotliar considered the coherence-incoherence crossover in the pnictides using LDA-DMFT.
Relevant papers on the thermopower and Hall coefficient of the pnictides that I became aware of this week include those of David Mandrus' group and Paul Canfield's group.
- the resistivity, Hall coefficient, and thermopower can have a non-monotonic temperature dependence
- with increasing temperature the resistivity can smoothly increase to values much larger than the Mott-Ioffe-Regel limit (h2 a/e ~ 1 mohm-cm)
- at temperatures of order T0 the thermopower can reach values as large as kB/e ~ 50 microV/K
- above temperatures of order T0 the Drude peak in the frequency dependent conductivity collapses and the associated spectral weight shifts to higher frequencies
- most of the spectral weight in the frequency dependent conductivity is at high frequencies
All of the above features in the transport are captured by a dynamical mean-field theory (DMFT) treatment of a range of lattice Hamiltonians such as the Hubbard model and Anderson lattice model. These issues are discussed in more detail in a paper Jaime Merino and I wrote 10 years ago. The figure below illustrates how sensistive the thermopower is to the destruction of quasi-particles.
 A recent paper by Haule and Kotliar considered the coherence-incoherence crossover in the pnictides using LDA-DMFT.
A recent paper by Haule and Kotliar considered the coherence-incoherence crossover in the pnictides using LDA-DMFT.Relevant papers on the thermopower and Hall coefficient of the pnictides that I became aware of this week include those of David Mandrus' group and Paul Canfield's group.
Monday, June 8, 2009
Organic superconductor session at GRC
Here are the slides (plus extras) I will show when I am discussion leader for the session on organic superconductors tonight.
Ironing out my ignorance
Before going to a conference and experiencing information overload it is worth thinking through what one is hoping to learn.
One thing I am looking forward to at the GRC on superconductivity is getting up to speed on the new iron pnictide superconductors.
Some of the questions I have are:
One thing I am looking forward to at the GRC on superconductivity is getting up to speed on the new iron pnictide superconductors.
Some of the questions I have are:
- Is there a universal phase diagram?
- What is the superconducting pairing symmetry?
- What are the experimental signatures of strong electronic correlations?
- Is there a pseudogap?
- Is the quality/purity of the samples high enough we can be confident that experimentalists are measuring what they claim on what they claim?
- What is the minimal quantum many-body Hamiltonian that can describe these materials? How many bands are necessary?
- Is there an variational wave function that captures the essential physics of the competition between the different ground states?
- What are the outstanding unresolved questions?
Sunday, June 7, 2009
Mapping out the pseudogap with interlayer magnetoresistance
Given the success described in the prevous post, an important question I have been wondering about the last couple of years is whether angle-dependent magnetoresistance (ADMR) can be used to detect and quantify the anisotropy of a pseudogap? I believe the answer is yes, based on recent calculations by Michael Smith, described in this preprint. Michael and I derived an expression for the interlayer magnetoresistance as a function of the direction of the tilted field, including the effects of anisotropies in all Fermi surface quantities including the pseudogap. We found a pseudogap can have significant effects on ADMR. As the temperature decreases the interlayer conductivity is dominated by the parts of the Fermi surface near the nodes of the pseudogap. This reduces the amplitude of variation in the magnetoresistance as the direction of the component of the field parallel to the layers changes. As the magnitude of the pseudogap increases the anisotropy becomes dominated by the anisotropy of the pseudogap rather than by the anisotropy of the intralayer Fermi velocity. This is illustrated in the Figure below which is a polar plot of the magnitude of the interlayer resistivity (for a band structure similar to that of overdoped Tl2201) as a function of the direction of the field parallel to the layers.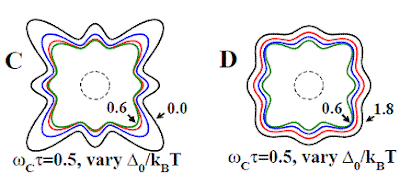
Our results should make it possible to determine the magnitude and anisotropy of the pseudogap in overdoped cuprates. This could answer outstanding questions about the pseudogap and the cuprate phase diagram that I described in a previous post.
There is some experimental evidence for a pseudogap in some organic charge transfer salts, the new iron pnictide superconductors , electron doped cuprates, and the layered heavy fermion compounds CeMIn5 [M=Co, Rh, Ir]. Hopefully, this work will stimulate more experimentalists to use this powerful probe of intralayer Fermi surface anisotropies.

Our results should make it possible to determine the magnitude and anisotropy of the pseudogap in overdoped cuprates. This could answer outstanding questions about the pseudogap and the cuprate phase diagram that I described in a previous post.
There is some experimental evidence for a pseudogap in some organic charge transfer salts, the new iron pnictide superconductors , electron doped cuprates, and the layered heavy fermion compounds CeMIn5 [M=Co, Rh, Ir]. Hopefully, this work will stimulate more experimentalists to use this powerful probe of intralayer Fermi surface anisotropies.
A powerful probe for mapping out Fermi surface properties in strongly correlated electron materials
A few years ago Malcolm Kennett and I developed a theoretical formalism that enabled the extraction of information about Fermi surface properties of layered metals from an analysis of the dependence of interlayer magnetoresistance on the direction of the magnetic field. We then contacted Nigel Hussey to get feedback on our paper before we submitted it. It turned out Nigel and his experimental group in Bristol were pursuing similar ideas to extract new information about the temperature and anisotropy (around the intralayer Fermi surface) of the scattering rate in overdoped cuprate superconductors.
The figure below, from our Nature Physics paper, shows the dependence of the interlayer resistance on theta, the angle between the field and the normal to the layers of the metal. Solid lines are experimental data for an overdoped cuprate superconductor in a magnetic field of 45 tesla and at temperatures varying from 4 K to 55 K. The dashed line are the results of our
theoretical calculation which includes anisotropy in the scattering rate on the Fermi surface. The sample is overdoped, i.e. the superconducting transition temperature Tc=15K is much less than that of optimally doped material which has a Tc=95 K.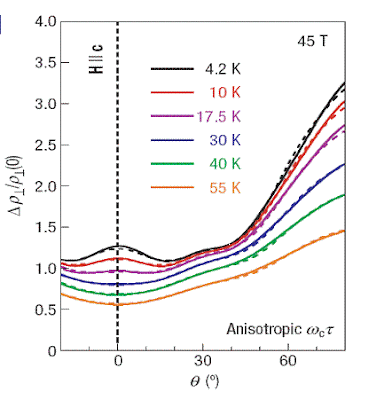 The Figure below shows the temperature dependence of the anisotropic component of the scattering rate extracted from the theoretical analysis of the experimental data.
The Figure below shows the temperature dependence of the anisotropic component of the scattering rate extracted from the theoretical analysis of the experimental data. I found this particularly interesting because the scattering rate showed there were "hot spots" at the same points on the Fermi surface as the nodes in the superconducting gap. This was exactly what was observed with ARPES in underdoped cuprates. However, our finding conflicted with Andrea Damascelli's groups ARPES results on the same material; they found "cold spots" in the overdoped cuprates. This difference has still not been resolved. But, it does underscore the value of this new magnetoresistance probe because it is a bulk measurement and has much higher "energy resolution" than ARPES.
I found this particularly interesting because the scattering rate showed there were "hot spots" at the same points on the Fermi surface as the nodes in the superconducting gap. This was exactly what was observed with ARPES in underdoped cuprates. However, our finding conflicted with Andrea Damascelli's groups ARPES results on the same material; they found "cold spots" in the overdoped cuprates. This difference has still not been resolved. But, it does underscore the value of this new magnetoresistance probe because it is a bulk measurement and has much higher "energy resolution" than ARPES.
The paper Malcolm and I wrote describing the theory wrote got some pedantic reviews at Physical Review Letters but was eventually published in Physical Review B.
In the next post I will discuss how this technique can also be used to study anisotropies in the pseudogap.
The figure below, from our Nature Physics paper, shows the dependence of the interlayer resistance on theta, the angle between the field and the normal to the layers of the metal. Solid lines are experimental data for an overdoped cuprate superconductor in a magnetic field of 45 tesla and at temperatures varying from 4 K to 55 K. The dashed line are the results of our
theoretical calculation which includes anisotropy in the scattering rate on the Fermi surface. The sample is overdoped, i.e. the superconducting transition temperature Tc=15K is much less than that of optimally doped material which has a Tc=95 K.
 The Figure below shows the temperature dependence of the anisotropic component of the scattering rate extracted from the theoretical analysis of the experimental data.
The Figure below shows the temperature dependence of the anisotropic component of the scattering rate extracted from the theoretical analysis of the experimental data. I found this particularly interesting because the scattering rate showed there were "hot spots" at the same points on the Fermi surface as the nodes in the superconducting gap. This was exactly what was observed with ARPES in underdoped cuprates. However, our finding conflicted with Andrea Damascelli's groups ARPES results on the same material; they found "cold spots" in the overdoped cuprates. This difference has still not been resolved. But, it does underscore the value of this new magnetoresistance probe because it is a bulk measurement and has much higher "energy resolution" than ARPES.
I found this particularly interesting because the scattering rate showed there were "hot spots" at the same points on the Fermi surface as the nodes in the superconducting gap. This was exactly what was observed with ARPES in underdoped cuprates. However, our finding conflicted with Andrea Damascelli's groups ARPES results on the same material; they found "cold spots" in the overdoped cuprates. This difference has still not been resolved. But, it does underscore the value of this new magnetoresistance probe because it is a bulk measurement and has much higher "energy resolution" than ARPES.The paper Malcolm and I wrote describing the theory wrote got some pedantic reviews at Physical Review Letters but was eventually published in Physical Review B.
In the next post I will discuss how this technique can also be used to study anisotropies in the pseudogap.
Friday, June 5, 2009
Am I HOMO- and LUMO-phobic?
Molecular orbital theory is a wonderful theory which has provided many qualitative insights into the electronic structure, optical and magnetic properties, and reactivity of organic molecules. Schematics such as that below can be extremely useful.

However, it is important to appreciate its limitations. In its simplest version it completely neglects interactions between electrons. Bear in mind molecular orbitals are just a theoretical construct. They do not actually exist. One can certainly calculate theoretically molecular orbital energies. However, these energies (e.g., of the HOMO and LUMO) can not be measured. What one can measure (and also calculate theoretically) are the energy of quantum states that do exist and obtain quantities such as
Hence, we should never expect molecular orbital theory to be quantitatively reliable and the figure above to be able to give a quantitative description of quantities such as open circuit voltages of solar cells based on donor-acceptor complexes.

However, it is important to appreciate its limitations. In its simplest version it completely neglects interactions between electrons. Bear in mind molecular orbitals are just a theoretical construct. They do not actually exist. One can certainly calculate theoretically molecular orbital energies. However, these energies (e.g., of the HOMO and LUMO) can not be measured. What one can measure (and also calculate theoretically) are the energy of quantum states that do exist and obtain quantities such as
- ionisation energy, I
- electron affinity, A
- electrochemical oxidation potential
- electrochemical reduction potential
- energy of the lowest lying singlet excited state, E(S1)
- energy of the lowest lying triplet excited state, E(T1)
Hence, we should never expect molecular orbital theory to be quantitatively reliable and the figure above to be able to give a quantitative description of quantities such as open circuit voltages of solar cells based on donor-acceptor complexes.
Thursday, June 4, 2009
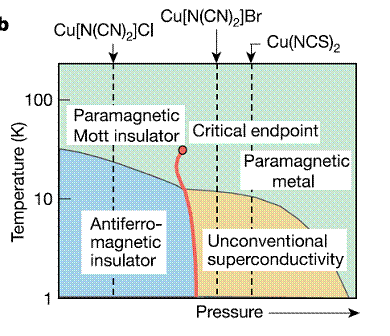
Organic charge transfer salts reveal a new universality class: the Mott metal-insulator transition
As mentioned in a previous post organic charge transfer salts have revealed rich new physics associated with strong electronic correlations. The family kappa-(BEDT-TTF)2X has the phase diagram below as a function of temperature and pressure. There is a first-order phase transition between a Mott insulator and a metal (which becomes superconducting below about 12 K. The first-order transition line ends a critical point at about 40 K.
 In 2005, Kagawa, Kawamoto, and Kanoda published a beautiful paper in Nature which did a scaling analysis of the conductivity near the critical point. From the figure below they could the extract critical exponents show (delta,beta,gamma)=(2,1,1). These values did not
In 2005, Kagawa, Kawamoto, and Kanoda published a beautiful paper in Nature which did a scaling analysis of the conductivity near the critical point. From the figure below they could the extract critical exponents show (delta,beta,gamma)=(2,1,1). These values did not
correspond to any known universality class. This is in distinct contrast to the critical exponents found for the corresponding metal-insulator transition for vanadium sesquioxide (V2O3) doped with chromium. In that case the exponents were those for the three dimensional Ising transition (liquid-gas transition).

Subsequently, Imada investigated theoretically how this universality class could emerge due to a marginal quantum critical region near a Mott transition. Misawa and Imada found how this class corresponded to the marginal point between the Ising transition and the topological transition of the Fermi surface.
I remember someone telling me there were problems with this theory
and so hopefully someone can write a comment about that.
So another example how the organic charge transfer salts are a
playground for emergent phenomena arising from quantum many-body physics.
 In 2005, Kagawa, Kawamoto, and Kanoda published a beautiful paper in Nature which did a scaling analysis of the conductivity near the critical point. From the figure below they could the extract critical exponents show (delta,beta,gamma)=(2,1,1). These values did not
In 2005, Kagawa, Kawamoto, and Kanoda published a beautiful paper in Nature which did a scaling analysis of the conductivity near the critical point. From the figure below they could the extract critical exponents show (delta,beta,gamma)=(2,1,1). These values did notcorrespond to any known universality class. This is in distinct contrast to the critical exponents found for the corresponding metal-insulator transition for vanadium sesquioxide (V2O3) doped with chromium. In that case the exponents were those for the three dimensional Ising transition (liquid-gas transition).

Subsequently, Imada investigated theoretically how this universality class could emerge due to a marginal quantum critical region near a Mott transition. Misawa and Imada found how this class corresponded to the marginal point between the Ising transition and the topological transition of the Fermi surface.
I remember someone telling me there were problems with this theory
and so hopefully someone can write a comment about that.
So another example how the organic charge transfer salts are a
playground for emergent phenomena arising from quantum many-body physics.
Tuesday, June 2, 2009
20 key concepts in thermodynamics and condensed matter
I gave my last lecture today. This is always a good feeling. Again I went over the 20 key ideas that I hoped they learnt in the course. The most important one, which we have to keep repeating is that in an non-isolated system whose state is defined by pressure and temperature, the Gibbs free energy G can never increase. Consequently, in the equilibrium state G must take the smallest possible value.
On my previous post on the 20 key concepts, Will Polik wrote a helpul comment:
On my previous post on the 20 key concepts, Will Polik wrote a helpul comment:
Related to concept 10 (free energy), I think that a key concept in the practical application of thermodynamics is the idea that "the entropy of the universe tends toward a maximum" is equivalent to "the Gibbs free energy of the system (at constant T and P) tends toward a minimum" and the corresponding statement about Helmholtz free energy. This allows one to use just the state properties of the system to determine the direction of change and equilibrium conditions, rather than having to worry about the entire universe!
Monday, June 1, 2009
Magnetic field induced superconductivity
Normally magnetic fields destroy superconductivity not help create it! However, in 2001 Uji and collaborators discovered that while the organic charge transfer salt (BETS)2FeCl4 had an insulating ground state applying a magnetic field parallel to the layers could create a metal, and for sufficiently high magnetic fields, superconductivity! This can be explained in terms of the exchange interaction between the magnetic Fe3+ ions and the pi electrons in the BETS molecules. When this exchange interaction is cancelled by the applied field (the Jaccarino-Peter effect, first proposed in the 1960's) the electron spins effectively see zero magnetic field.
I was very happy that in our paper Olivier Cepas, Jaime Merino, and I were able to predict the magnetic field range in which one should observe magnetic-field induced superconductivity for a specific material and this was subsequently observed.
One can tune between Mott insulating, metallic, and superconducting states by varying the magnetic field, temperature, or the relative concentration of magnetic Fe3+ ions and non-magnetic Ga3+ ions. This leads to a rich phase diagram such as that shown below. For a review see here.

Because the relevant field and temperature scales are so small these means that the superconducting and Mott insulating phase are very close in energy. i.e., within a few meV, which is orders of magnitude smaller than the energy scales in the underlying Hubbard Hamiltonian. Such a competition occurs naturally in RVB theory.
I was very happy that in our paper Olivier Cepas, Jaime Merino, and I were able to predict the magnetic field range in which one should observe magnetic-field induced superconductivity for a specific material and this was subsequently observed.
One can tune between Mott insulating, metallic, and superconducting states by varying the magnetic field, temperature, or the relative concentration of magnetic Fe3+ ions and non-magnetic Ga3+ ions. This leads to a rich phase diagram such as that shown below. For a review see here.

Because the relevant field and temperature scales are so small these means that the superconducting and Mott insulating phase are very close in energy. i.e., within a few meV, which is orders of magnitude smaller than the energy scales in the underlying Hubbard Hamiltonian. Such a competition occurs naturally in RVB theory.
Subscribe to:
Posts (Atom)
Thermodynamics and emergence
Novelty. Temperature and entropy are emergent properties. Classically, they are defined by the zeroth and second laws of thermodynamics, re...
-
Is it something to do with breakdown of the Born-Oppenheimer approximation? In molecular spectroscopy you occasionally hear this term thro...
-
I welcome discussion on this point. I don't think it is as sensitive or as important a topic as the author order on papers. With rega...
-
Nitrogen fluoride (NF) seems like a very simple molecule and you would think it would very well understood, particularly as it is small enou...

