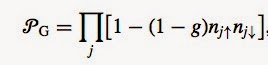The biggest challenge in education today?

This post was stimulated by attending a talk about (yet another) review of the curriculum in Australian schools. The talk and following discussion was conducted according to the Chatham House rule, which I had never encountered before.

Previously I wrote about the iron triangle in education: access, cost, and quality.

What is the role and significance of curriculum in education?
I think it is helpful to make some clear distinctions in roles, responsibilities, and desired outcomes.

1. Students learning.
This is what it is all about! It is important to distinguish this from students passing exams, attending lectures, or completing tasks.

2. Effective teachers.
They need to be passionate and competent, both about their subject and their students.

3. Curriculum and resources.
This also includes textbooks, course handbooks, online resources, buildings, libraries, equipment, laboratories, computers....

4. Policies and administrative procedures.
This includes hiring and firing, retaining, training, and rewarding teachers. Funding.
Paperwork. Oversight and accountability. Assessment/grading. Course profiles.

I think the biggest challenge in education today is to have a smooth and efficient flow from 4 to 1. Unfortunately, sometimes/often 4. and even 3. can actually hinder 2 and stymie 1.

I claim that doing 2, 3 and 4 well are neither necessary nor sufficient conditions for 1 to happen.

A good teacher is not sufficient for student learning. If the students are not motivated or do not have the appropriate background and skills, it does not matter how good the teacher is, the students won't learn.
Some students (admittedly a minority) can be even learn with a terrible teacher. If they are highly motivated and gifted they will find a way to teach themselves.
Great teachers can be effective without good textbooks or fancy buildings or career reward structures.
A great textbook and curriculum and fancy facilities won't help if the teacher is a dud.
Strong accountability structures with high quality testing and ranking of students, teachers, and schools do not guarantee learning. Teachers will teach to the test. Bad teachers and schools will put on an amazing show when they are "inspected.".

A major problem is that there are influential individuals, organisations, and bureaucracies that strongly believe (or pretend to believe) that 4 and/or 3 are necessary and sufficient for learning to happen. This leads to a distorted allocation of resources and heavy administrative burdens that are counter productive.

The Mott transition as doublon-holon binding

What is the "mechanism" and definitive signatures of the Mott metal-insulator transition?
If there is an order parameter, what is it?

Consider a single band Hubbard model at half-filling.
As U/t increases there is a transition from a metal to an insulator.
The critical value of U/t is non-zero except for cases (e.g. one dimension or the square lattice) where there is perfect Fermi surface nesting of the metal state.

Here is one picture of the transition: the metal to insulator transition is due to binding of holons and doublons. This is advocated by Yokoyama and collaborators and summarised in the Figure below (taken from this paper). At half filling there are equal numbers of holons and doublons.

In the metallic state (left) the holons and doublons are mobile. In the insulating state (right) holons and doublons are bound together on neighbouring sites.

Evidence for this picture comes from numerical simulations. Yokoyama, Ogata, and Tanaka consider the following variational wave function.

P_G is a partial Gutzwiller projection

A Monte Carlo treatment gives the graph below for the variational parameter mu as a function of U/t.

                                 

Clearly near the critical U there is a large discontinuous change in mu, reflecting a large change in the nearest neighbour correlations of holons and doublons.
In contrast, at the transition there is only a small change in the variational parameter g, reflecting the fact that at the transition there is only a small change in the double occupancy [doublon density].

A recent preprint by Sato and Tsunetsugu reports investigations of the Hubbard model on the triangular lattice using cluster DMFT. The figure below shows how P^dh, the probability of a doublon and holon being on neighbouring sites (normalised to the product of the density of holons and that of doublons),  changes significantly at the transition. In contrast, there are only small changes in the doublon density (shown in the inset).

A slave boson theory of the holon-doublon binding transition has recently been given by Sen Zhou, Yupeng Wang, and Ziqiang Wang.

What are some alternative pictures for the Mott transition?

Slater
The transition arises due to Fermi surface nesting and the insulating state is associated with the opening of a band gap due to new commensurability's associated with antiferromagnetic (or spin-density wave) order. Importantly, the insulator requires magnetic order.
This is a weak-coupling picture.

Brinkman-Rice 
[equivalent to slave bosons = Gutzwiller approximation on a Gutzwiller variational wave function]
As U increases the band width is renormalised until it (and the double occupancy) shrinks to zero at the transition. This is a second-order transition. No magnetic order is required for the insulator.

Dynamical-mean field theory
I find this hard to summarise. Interactions produce lower and upper Hubbard bands. Self-consistent stabilisation of the metal is associated with Kondo screening of local moments by the bath of delocalised electrons, leading to a coherent band near the chemical potential. The spectral weight in this band shrinks with increasing interaction U. The transition is first order. No magnetic order is required for the insulator. This is a completely local picture.

I thank Peter Prelovsek (who is currently visiting me) for bringing this problem to my attention.

When is water quantum? II

A previous post focused on quantum effects largely associated with hydrogen bonding associated with the O-H stretch vibration. Here, I consider effects largely associated with angular motion, known as librational modes.

Feynman Path Integral computer simulations performed by Peter Rossky, Bruce Berne, Greg Voth, and Peter Kusalik have led to the following key ideas.

1. Quantum water is less structured than classical water.

This is seen in the figure below taken from a 2004 paper by Hernandez de la Pena and Kusalik.

2. This is largely do to quantisation of orientational rather than translational degrees of freedom.

The clear evidence for this is from Kusalik's path integral simulations. There, the water molecules are rigid and only the orientational motion of the molecules is quantised. Similar results for the structure factor, (translational) diffusion constant, and orientational relaxation times (and their isotope effects) are obtained from simulations with flexible molecules and quantised translational modes.

3. Many of these quantum effects are similar to those of classical water with a higher temperature by 50 K. 

The figure below taken from a 2005 paper by Hernandez de la Pena and Kusalik. The structure functions are virtually identical for quantum water at 0 degrees C and classical water at 50 degrees C.

The temperature dependence of the potential energy is shown below. The quantum energy is larger than the classical by about 350 cm^-1.

N.B. one should not use this result to justify the claim that ALL quantum effects are similar to raising the temperature by 50 K. For example, none of the quantum effects discussed in the earlier post can be understood in these terms.

What is going on?

Here is one idea about the essential physics. I think it is similar to earlier ideas going back to Feynman and Hibbs (page 281) about effective "classical potentials", and discussed in detail by Greg Voth.

Consider a simple harmonic (angular/torsional) oscillator of frequency Omega and moment of inertia I at temperature T. The RMS fluctuation in the angle Phi are given below for the quantum and classical cases.

The two temperature dependences of the quantum case [purple curve] and classical curve [straight red line] are plotted below. The temperature [horizontal scale] is in units of the zero point energy.  The vertical scale is in units of the zero-point motion.

The RMS is about the same [horizontal line] when the quantum temperature (273 K) is such that
Omega/k_B T ~ 3 and the classical temperature is about 15 per cent larger.

This suggests that Omega ~ 3 k_B T ~ 600 cm^-1.

Is this reasonable?

The figure below shows the spectrum of the librational modes.

This frequency scale is also consistent with the differences in potential energy.

How do the quantum fluctuations lead to softening of the structure?

Quantum fluctuations lead to "swelling" of the polymer beads in the discrete path integral or the new effective classical potential, a la Feynman-Hibbs/Voth...
This swelling reduces the effective interaction between molecules and reduces structure

Some of the papers mention the role of tunnelling.
It is not clear to me what this is about.
Can anyone clarify?

Temperature dependence of the resistivity is not a definitive signature of a metal

When it comes to elemental metals and insulators, a simple signature to distinguish them is the temperature dependence of the electrical resistivity.
Metals have a resistivity that increases monotonically with increasing temperature.
Insulators (and semiconductors) have a resistivity that decreases monotonically with increasing temperature.
Furthermore, for metals the temperature dependence is a power law and for insulators it is activated/exponential/Arrhenius.
This distinction reflects the presence or absence of a charge gap, i.e., energy gap in the charge excitation spectrum.
Metals are characterised by a non-zero value of the charge compressibility

and a non-zero value of the (one-particle) density of states at the chemical potential (Fermi energy for a Fermi liquid).

However, in strongly correlated electron materials the temperature dependence of the resistivity is not a definitive signature of a metal versus an insulator.

The figure below shows the measured temperature dependence of the resistivity (on a logarithmic scale)  of the organic charge transfer salt kappa-(ET)2Cu2(CN3) for several different pressures. At low pressures it is a Mott insulator and for high pressures a metal (and a superconductor at low temperatures).

The data is taken from this paper.
Note that at intermediate pressures the resistivity is a non-monotonic function of temperature, becoming a Fermi liquid and then a superconductor at low temperatures.
Some might say that the system undergoes an insulator-metal transition as the temperature is lowered.
I disagree.
The system undergoes a smooth crossover from a bad metal to a Fermi liquid as the temperature is lowered. It is always a metal, i.e. there is no charge gap.

This view is clearly supported by the theoretical results shown below (taken from this preprint) and earlier related work based on dynamical mean-field theory (DMFT).

The graph below is the calculated temperature dependence of the resistivity for a Hubbard model, for a range of interaction strengths U [in units of W, the half band width].
Note, the non-monotonic temperature dependence for values of U for which the system becomes a bad metal, i.e. the resistivity exceeds the Mott-Ioffe-Regel limit.

But, for the temperature and U range shown the system is always a metal.
This is clearly seen in the calculated non-zero value of the charge compressibility, shown below.

Aside: In the cuprates the question of whether the pseudogap phase is a metal, insulator, or semi-metal is a subtle question I do not consider here.

I thank Nandan Pakhira for emphasising this point to me and encouraging me to write this post.

Is there a quantum limit to diffusion in quantum many-body systems?

Nandan Pakhira and I recent completed a paper
Absence of a quantum limit to charge diffusion in bad metals

This work was partly motivated by

- a recent proposal, using results from the AdS-CFT correspondence, by Sean Hartnoll that there was a quantum limit to the charge diffusion constant in bad metals,

- experimental observation and theoretical calculations of a limit to the spin diffusion constant in cold atom fermions near the unitarity limit.

We calculated the temperature dependence of the charge diffusion constant in the metallic phase of a Hubbard model using Dynamical Mean-Field Theory (DMFT).

The figure below shows  the temperature dependence of the charge diffusion constant for a range of values of the Hubbard U. The temperature and energy scale is the half-bandwidth W. The Mott insulator occurs for U larger than about 3.4 W.

Violations of Hartnoll's bound occurs in the same incoherent regime as violations of the Mott-Ioffe-Regel limit on the resistivity.

We also find that the charge diffusion constant can have values orders of magnitude smaller than the cold atom bound on the spin diffusion constant.

We welcome discussion and comments.

The puzzling magnetoresistance of graphite

At the Journal Club on Condensed Matter, Jason Alicea has a stimulating commentary on an interesting experimental paper,

Two Phase Transitions Induced by a Magnetic Field in Graphite
Benoît Fauqué, David LeBoeuf, Baptiste Vignolle, Marc Nardone, Cyril Proust, and Kamran Behnia 

In the experiment, the temperature dependence of the resistance of graphite [stacks of layers of graphene] is measured with magnetic fields perpendicular to the layers for fields up to 80 Tesla.
[n.b. the high field! This is a pulsed field.]
It is estimated that above 7.5 Tesla all the graphene layers are in their lowest Landau level.

The figure below shows a colour shaded plot of the interlayer resistance [on a logarithmic scale] as a function of temperature and magnetic field.

This is highly suggestive of a phase diagram and that several phase transitions occur as a function of magnetic field. This is highly appealing (seductive?) because there are theoretical predictions [reviewed by Alicea] of such phase transitions, specifically into charge density wave states (CDW).
Furthermore, there are even proposals of (sexy) edge states in directions perpendicular to the layers.

However, I am not so sure. I remain to be convinced that there are thermodynamic phase transitions. The experiment is observing changes in interlayer transport properties.
Here are my concerns.

1. The conduction is metallic within the layers and insulating perpendicular to the layers. This is clearly seen in the figure below showing resistivity versus temperature at a field of 47 Tesla. In particular, note that the resistance parallel to the layers [red squares and left linear scale] is essentially temperature independent. In contrast, the resistivity perpendicular to the layers [blue squares and right logarithmic scale] becomes activated, below about 6 K, with an energy gap of about
2.4 meV=25 K.

As Alicea points out, this is very strange. Normally, a charge gap (like in a quasi-one-dimensional CDW) will produce activated transport in all directions.

2. Even at lower fields, i.e. below 10 Tesla, the interlayer magnetoresistance of graphite is anomalous. In a simple Fermi liquid, there is no orbital magnetoresistance when the magnetic field and current are parallel. Pal and Maslov consider this problem of longitudinal magnetoresistance. With a simple model calculation using a realistic band structure for graphite they obtain a saturating magnetoresistance of about 20 percent, whereas the experimental value is orders of magnitude larger. 

3. A large interlayer magnetoresistance when the magnetic field is parallel to the current (and so there is no Lorentz force) is reminiscent of unusual magnetoresistance seen in a wide range of correlated electron materials.

4. Confusion about "insulating" magnetoresistance has occurred before. I discussed this earlier in the context of the large orbital magnetoresistance of a transition metal oxide PdCoO2. Just because the resistance increases with decreasing temperature at a fixed field does not mean that the system is in an insulating state. Copper does this! From my point of view, this was one of the problems with the exotic claims made by Anderson, Clarke, and Strong in the 1990s of non-Fermi liquid states in Bechgaard salts [see for example this PRL and Science paper]. They never actually calculated magnetoresistance but made claims about field-induced "confinement" phase transitions. Understanding these angle-dependent magnetoresistance experiments remains an open problem.

5. The results are sample dependent, although qualitatively consistent. Different results are obtained for different forms of graphite (kish and HOPG). Furthermore, in layered metals, it is difficult to measure the interlayer and intralayer resistivity. Due to impurities, stacking defects, and contact misalignment the electrical current path will inevitably contain some mixture of interlayer and intra-layer paths.

6. I am a bit confused about the argument concerning edge states. The authors suggest that the fact that the interlayer resistivity saturates at low temperatures (i.e. is no longer activated) is evidence for edge states. It is not clear to me why there is no evidence of the gap in the interlayer resistance. They say something about the mixing of interlayer and intralayer currents due to stacking defects, but I did not find it a particularly clear argument.

So what is the most likely explanation? I am not sure. Perhaps, there are no phase transitions. The role of the field may be to somehow decouple the layers. There are several comparable energy scales involved, particularly due to the semi-metal character of graphite.

Thermodynamic experiments are desirable. Calculations of the interlayer and interlayer resistance within CDW models need to be done too.

The challenge of writing books on water

Biman Bagchi has just published a new book,
Water in Biological and Chemical Processes: From Structure and Dynamics to Function 

Cambridge University Press sent me a complimentary copy to review. I am slowly working through it and will write a detailed review when I am done.

I think this is a very challenging subject to write a book on for at least three reasons. First, the scope of the topic is immense. Furthermore, it is multi-disciplinary spanning physics, chemistry, and biology, with a strong interaction between experiment, theory, and simulation. Second, although there have been some significant advances in the last few decades there is real state of flux, with a fair share of controversies, advances, and fashions. Finally, which audience do you write for? Experimental biochemists or theoretical physicists or somewhere in between.

Although this is an incredibly important and challenging topic few authors have taken up the challenge. One who has is Arieh Ben-Naim

Molecular Theory of Water and Aqueous Solutions, Part I: Understanding Water (2009)

Molecular Theory of Water and Aqueous Solutions Part II: The Role of Water in Protein Folding, Self-Assembly and Molecular Recognition (2011)

This was a topic of great interest to my late father. He wrote two comprehensive reviews with John Edsall, published in Advances in Biophysics

Water and proteins. I. The significance and structure of water; its interaction with electrolytes and non-electrolytes (1977) [does not seem to be available online]

Water and proteins. II. The location and dynamics of water in protein systems and its relation to their stability and properties (1983)

Classic earlier books include:

The Structure and Properties of Water
 by David Eisenberg and Walter Kauzmann
(1969, reissued in 2002 by Oxford UP in their Classic Texts in the Physical Sciences)

A seven volume series, Water: A comprehensive treatise, edited by Felix Franks

At the popular level there is
Life's Matrix: A Biography of Water 
(2001) by Philip Ball

An efficient publication strategy

Previously I posted about my paper submission strategy.
A recent experience highlighted to me the folly of the high stakes game of going down the status chain of descending impact factors:
Nature -> Science -> Nature X, PNAS -> PRL, JACS -> PRB, JCP.

Two significant problems with this game are:
1. A lot of time and energy is wasted in strategising, rewriting, reformatting, and resubmitting at each stage of the process. Furthermore, if there are multiple senior authors each stage can be particularly slow.
2. Given the low success rates the paper often ends up in PRB or a comparable journal (J. Chem. Phys., J. Phys. Chem.) anyway!

I have followed this route and it has been a whole year between submission and publication.

In contrast, on 28 July I submitted a paper as a regular article to J. Chem. Phys. and it appeared online on 10 September!
Six weeks!
I have also had papers published in PRA and PRB much faster than in PRL.

Why is speedy publication valuable?

• The sooner it is published, the sooner that some people, particularly chemists, will take it seriously.
• The time and mental energy that is saved can be spent instead  doing more research and writing more papers.
• A few months can be the difference so you can list the paper as published on the next job application, grant report, or grant application.
• The sooner it is published the sooner it will start getting cited. 

Furthermore, in the long run, the value of the science carries the day. If the research is valuable and significant it will have a real impact, regardless of where it is published. Papers make the impact not the journals. If I look at my own publication list [particularly on the 5+ years time scale] there is not a lot of correlation between journal impact factor, real scientific impact [the most desirable citations] and total citation numbers.

Reflecting on teaching evaluations

Getting feedback from students via formal evaluations at the end of a course can be helpful, encouraging or discouraging, frustrating, satisfying ...

A few weeks ago I got my evaluations for a course I taught last semester. Here are my reflections. First, given there were only 5 they should be taken with a grain of salt! They were very positive which was quite encouraging. They aren't always...

I was particularly encouraged that students noticed and appreciated several things I worked on and increasingly emphasise.

• Giving the big picture and trying to put everything in that context.
• Having a good textbook [Ashcroft and Mermin, in this case] and following it closely.
• Making order of magnitude estimates.

One student pointed out how my treatment of semiconductors was not as clear at the earlier material. I agree! This was the first time I had taught that part of the course. In contrast, most of the other material I have taught 5-10 times before. Some of it relates closely to my research and I have thought about deeply. This shortcoming  also reflects that I am still not comfortable with the semiconductor material. I can "say the mantra" of how a p-n junction works but I still don't really understand it. I am not surprised that the students picked up on this.

Over the years I have co-taught courses with colleagues who have varied significantly in experience, ability, enthusiasm, effort, ...
I have noticed that my evaluations correlate with those of my co-teacher. Students make comparisons. If I co-teach with an experienced gifted teacher students are more critical of me and my evaluations go down. On the other hand if I co-teach with a younger less experienced colleague or an older colleague who has no interest in teaching my scores go up.
The take home point is not to get too discouraged in the former case and not to let it go to my head in the latter case.

The evaluations also seem to correlate with the ability, background, attitudes, expectation levels, and motivation levels of the students. Do they see me as an ally or an adversary? Given what I have observed during the semester I am usually not too surprised by the evaluations.

When is water quantum?

Many properties of bulk water, including its many anomalous properties, can be described/understood in terms of the classical dynamics of interacting "molecules" that consist of localised point charges. However, there is more to the story. In particular, it turns out some of the success of classical calculations arise from a fortuitous cancellation of quantum effects. Some quantum effects can just be mimicked by using a higher temperature or a softer potential in a classical simulation.

Properties to consider include thermodynamics, structure, and dynamics. Besides bulk homogeneous liquid water, there is ice under pressure, and water in confined spaces, at surfaces, and interacting with ions, solutes, and biomolecules.

Distinctly quantum effects that may occur in a system include zero-point motion, tunnelling, reflection at the top of a barrier, coherence, interference, entanglement, quantum statistics, and collective phenomena (e.g. superconductivity). As far as I am aware only the first two are relevant to water: they involve the nuclear degrees of freedom, specifically the motion of hydrogen atoms or protons. A definitive experimental signature of such quantum effects in seen by substitution of hydrogen with deuterium.

Although there have been exotic claims of entanglement, from both experimentalists and theorists, I think these are based on such dubious data and unrealistic models they are not worthy of even referencing. More positively, there may also be some collective tunnelling effects involving hexagons of water molecules, as described here.

When are quantum nuclear effects significant? 
What are the key physico-chemical descriptors?

I believe there are two:
the distance R between a proton donor and acceptor in a hydrogen bond and
epsilon, the difference between the proton affinity of the donor and the acceptor.

Quantum nuclear effects become significant when both R is less than 2.6 Angstroms and epsilon is less than roughly 20 kcal/mol.

In bulk water at room temperature the average value of R is about 2.8 Angstroms and epsilon is of the order of 20 kcal/mol and so quantum nuclear effects are not significant for properties that are dominated by averages. However, there are significant thermal fluctuations than can make R as small at 2.4 Angstroms and epsilon smaller, for times less than hundreds of femtoseconds. More on that below. Furthermore, when water interacts with protons, to produce entities such as the Zundel cation, or with biomolecules, the average R can be as small at 2.4 Angstroms and epsilon can be zero. Also, in high pressure phases of ice (such as in Ice X) average values of R of order 2.4 Angstrom  occur.

This way of looking at quantum nuclear effects is discussed at length in this paper.

[Image from here]

What are the key organising principles for understanding quantum nuclear effects?

I proposed before these two.

1. Competing quantum effects: O-H stretch vs. bend

Hydrogen bonding changes vibrational frequencies and thus the zero-point energy. As the H-bond strength increases (e.g. due to decreasing R) the O-H stretch frequency decreases while the O-H bend frequencies increases. These changes compete with each other in their effect on the total zero-point energy. Also, the quantum corrections associated with the two types of vibrations have the opposite sign reducing the total quantum effects.
I think this idea was first clearly stated by Markland, Habershon, and Manolopoulos.

2. Dynamics dominated by rare events

For example, consider proton transfer in water. When R is at the average value of 2.8 Angstroms the energy barrier is very large. However, if there a very short fluctuation in R so that it reduces to 2.4 Angstroms the barrier disappears and the proton transfers.

What are the implications of these two organising principles for computer simulations?

Pessimism and caution!

1. Subtracting two numbers of about the same size can be error prone.
Suppose that we can calculate the quantum effects of each of the vibrational modes to an accuracy of about 10 per cent. Then we add the contributions (picking some representative numbers):
100 - 50 - 30 = 20. The problem is that the total error is about +/-20.

2. The probability of the rare events is related to the tails of the nuclear wave function. The problem is that this is very sensitive to the exact form of the effective potential energy surface (PES) for the nuclear motion. Tunneling is very sensitive to the height and shape of energy barriers. The problem is that is very difficult, particularly for hydrogen bonding, to calculate these PES accurately, especially at the level of Density Functional Theory. These issues are nicely illustrated in a recent paper by Wang, Ceriotti, and Markland.

This post is motivated by preparing to be part of a working group on quantum water at a Nordita workshop.

My questions are:
Is the picture above valid? Is it oversimplified? Are there exceptions?
Are the two organising principles valid and important? Are there other relevant principles?

Double proton transfer rates vs. distance

There is a nice paper
Tautomerism in Porphycenes: Analysis of Rate-Affecting Factors
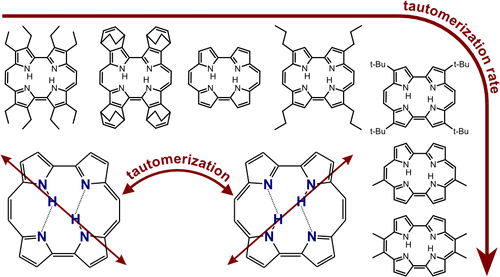
Piotr Ciąćka, Piotr Fita, Arkadiusz Listkowski, Michał Kijak, Santi Nonell, Daiki Kuzuhara, Hiroko Yamada, Czesław Radzewicz, and Jacek Waluk

They look at nineteen different porphycenes, which means that R, the distance between the nitrogen atoms that donate and accept a proton varies.
[This is a testimony to the patience and skill of synthetic organic chemists to produce 19 different compounds.]

The rate of tautomerization [i.e. double proton transfer] can be measured my monitoring the time dependence of the fluorescence anisotropy because the transition dipole moment of the two tautomers is in different directions, as illustrated below, in the graphical abstract of the paper.

The key result is below: the rate of tautomerization [i.e. double proton transfer] versus R. Note the vertical scale varies by three orders of magnitude.

For single hydrogen bonds many correlations between R and observables such as bond lengths and vibrational frequencies have been observed.

The natural explanation for this correlation is that as R decreases so does the energy barrier for double proton transfer. At least at the qualitative level this is captured by my simple diabatic state model for double proton transfer [which just appeared in J. Chem. Phys.]. However, my model only predicts a correlation is the ratio of the proton affinity of the donor with one and two protons on the donor does not change as one makes the chemical substitutions that change R.

(I think) all these experiments are done at room temperature in a solvent.
Two open questions concern whether the double proton transfer is sequential or concerted, and whether it is activated or involves tunnelling. At low temperatures in supercooled jets there is evidence of tunnel splitting and concerted transfer.

A few tips on getting organised

I would not claim to be the most organised person. I know I can do better. But, I also know I struggle less than some. Here are a few things that help me to avoid chaos. I don't do all of them all the time, but they are good to aim for.

Just say no.
The more responsibilities you take on and the busier you get and the harder it is to juggle everything, keep up, think clearly, set priorities, avoid the tyranny of the urgent....

A clear desk
I am more relaxed, focused, and productive, if the only thing I have on the desk in front of me is what I am actually working on. Move the piles of other stuff somewhere else, out of view.

Google Calendar
I have a work calendar and a personal one. I include all my weekly meetings and obligations.
Everyone I work with can see the work calendar and knows what I am up to. They can also see "busy" if there is something in the personal one. My family sees both.

Keep the schedule
Once something is in the calendar it is more or less fixed. Only in exceptional circumstances do I reschedule.

Papers for Mac
Any paper I download goes in there. Mostly I only print it if I am going to read it now. Papers is great for searching and finding stuff.

The paperless office
Sorry, I can't do it. Anything that requires a detailed and thoughtful reading I have to read in hard copy. But, ...

The paper recycling bin is your friend
I only save papers I am likely to read again. All the admin stuff goes in a box below my desk that then ends up in the recycling bin.

A moratorium on buying new bookcases and filing cabinets
I already have too many, both at work and home. So, if I buy more books or file more papers I have to get rid of some existing ones.

email
Turn it off. Try to only look at it a few times a day.
I have folders I do occasionally file stuff in.
I have not yet managed to use tags such as to remind me to act on certain things.

to do list
I have a long one on the computer, and so it is easily edited and updated.
I don't look at it often enough, out of guilt and frustration. But it is a useful reminder and it does feel good to cross stuff off.
On busy days I do hand write a schedule for the day.

Mobile phone
I don't use one.

I could do a lot better. I welcome others to share what they have found helpful.

The challenge of coupled electron-proton transfer

There is a nice helpful review
Biochemistry and Theory of Proton-Coupled Electron Transfer 
Agostino Migliore, Nicholas F. Polizzi, Michael J. Therien, and David N. Beratan

Here are a few of the (basic) things I got out of reading it (albeit on a long plane flight a while ago).

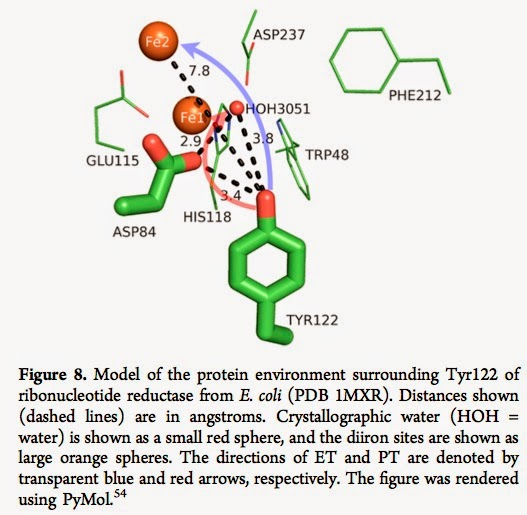
There are a diverse range of biomolecules where coupled electron-proton transfer plays a key role in their function. The electron transfer (ET) and proton transfer (PT) are usually spatially separated. [See blue and red arrows below].

There are fundamental questions about whether the transfer is concerted or sequential, adiabatic or non-adiabatic, and how important the protein environment (polar solvent)  is.

Often short hydrogen bonds are involved and so the nuclear degrees of freedom need to be treated quantum mechanically, in order to take into account tunnelling and/or zero-point motion.

Diabatic states are key to understanding and theoretical model development.

Although there are some "schematic" theories, they involve some debatable approximations (e.g. Fermi's golden rule), and so there is much to be done, even at the level of minimal model Hamiltonians.

Summarising generic progress

I would like to review some important new results on topic X. Several recent studies using some complicated new experimental technique together with large computer simulations have led to new insights and understanding. This is a major advance in the field and attracting significant attention. But there are still many open questions and there remains much work to be done.

Did you learn anything from this "review" beyond that X is a hot topic that is generating lots of papers?
Unfortunately, I find many "News and Views" or "Perspective" pieces and review articles read a bit like the paragraph above. I would really like to know what specific new insights have been gained and what the open questions are.

Why do we often degenerate to the generic?
It is actually hard work to figure out what the specific insights are and to clearly communicate them, particularly in a few sentences.

Killing comparisons II.

Previously I wrote about the danger of comparing oneself to your peers. It can easily lead to discouragement, anxiety, and a loss of self-confidence.

It is also unhelpful for students and postdocs to compare their present advisor/supervisor/mentor  to past advisors.
It is also unhelpful for a supervisor to compare their current students/postdocs to previous ones.

Early in his career Professor X had an absolutely brilliant student Y who made an important discovery. [Decades later X and Y shared a Nobel Prize for this discovery.] Apparently, X compared all his later students to Y, and could not understand why they could not be as good as Y. Sometimes he even let the students know this.

I have also known people who have had an exceptionally helpful undergrad/Ph.D advisor but then were always unhappy with their graduate/postdoc advisor because they just weren't as helpful.

Making comparisons is a natural human tendency. Sometimes I struggle with it. But, I try not to. It is only a route to frustration, to difficult relationships, and failed opportunities to help people develop.

Every individual has a different background, training, personality, gifting, and interests, leading to a diversity of strengths and weaknesses. Being a good student/postdoc involves innate intelligence, technical expertise, mathematical skills, computer programming, giving talks, getting along with others, writing, knowing the literature, time management, multi-tasking, planning, conceptual synthesis, understanding the big picture, being creative ....
Some of these will come very easily to some individuals. Some will really struggle.
The key is to accept each individual where they are at now and help them build on their strengths and realistically improve in their weak areas.

I think their are only two times when it is helpful and appropriate to make comparisons. Both should only be done in private. In writing letters of reference it may be appropriate and helpful to compare a student to previous ones. In deciding who to work with (e.g. for a postdoc) it is appropriate to research the advisor and compare them to other possible candidates. I meet too many students/postdocs who are struggling with an unhelpful advisor but never thought to find out what they were like before they signed up.

A course every science undergraduate should take?

Science is becoming increasingly inter-disciplinary.
Most science graduates do not end up working in scientific research or an area related to their undergraduate major.
Yet most undergraduate curricula are essentially the same as they were fifty years ago and are copies of courses at MIT-Berkeley-Oxford designed for people who would go on to a Ph.D and (hopefully) end up working in research universities.
Biology and medicine are changing rapidly particularly in becoming more quantitative.
How should we adapt to these realities?
Are there any existing courses that might be appropriate for every science major to take?

Sometimes my colleagues get upset that advanced physics undergrads don't know certain things they should [Lorentz transformations, Brownian motion, scattering theory, ....]. But, my biggest concern is that they don't have certain basic skills [dimensional analysis, sketching graphs, recognising silly answers,  writing clearly, ....]. These skills will be important in almost any job that has a quantitative dimension to it.

For the past few years Phil Nelson has been teaching a course at University of Pennsylvania that I think may "fit the bill." The associated textbook Physical Models of Living Systems will be published at the end of the year.

Previously, I have lavished praise on Nelson's book Biological Physics: Energy, Information, Life. I used it in a third year undergraduate biophysics course PHYS3170 and think it is one of the best textbooks I have every encountered. Besides clarity and fascinating subject material it has excellent problems [and solutions manual], makes use of real experimental data, has informative section headings, often discusses the limitations of different approaches, and uses nice historical examples.

The new book covers different material and focuses on some particular skills that any science and engineering major should learn, regardless of whether they end up working in biology or medicine or biophysics. Below I reproduce some of Nelson's summary.

Readers will acquire several research skills that are often not addressed in traditional courses:

• Basic modeling skills, including dimensional analysis, identification of variables, and ODE formulation.
• Probabilistic modeling skills, including stochastic simulation.
• Data analysis methods, including maximum likelihood and Bayesian methods.
• Computer programming using a general-purpose platform like MATLAB or Python, with short codes written from scratch.
• Dynamical systems, particularly feedback control, with phase portrait methods.

[Here modeling does not mean running pre-packaged computer software but developing simple physical models].

All of these basic skills, which are relevant to nearly any field of science or engineering, are presented in the context of case studies from living systems, including:

• Virus dynamics
• Bacterial genetics and evolution of drug resistance
• Statistical inference
• Superresolution microscopy
• Synthetic biology
• Naturally evolved cellular circuits, including homeostasis, genetic switches, and the mitotic clock.

This looks both important and fascinating. The Instructors Preface makes an excellent case for the importance of the course, including to pre-medical students. The Table of Contents illustrates not just the logical flow and interesting content but again uses informative section headings that summarise the main point.

So, what do you think?

Is this a course (almost) every science undergraduate should take?

Are there specific courses you think all students should take?