Will burning lots of coal lift people out of poverty?

A few months ago I attended a symposium at UQ on Energy in India. The talks can be viewed on Youtube. The one by Alexie Seller is particularly inspiring.

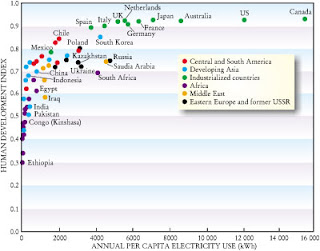
In the presentation of Chris Greig he showed a slide similar to that below with the title "Electricity affects Human well being".

He did not say it, but sometimes graphs like this are used to make claims such as "the more electricity people consume the better off they will be..."  or "the only way to lift people out of poverty is to burn more coal..."

Sometimes people show graphs that correlate GDP with energy consumption. But this one is better because it uses the Human Development Index, a multi-dimensional measure of human well being (as it includes life expectancy and education).

Two things are very striking about the graph.
First, the initial slope is very large. Second, the graph levels off quickly.
A little bit of electricity makes a huge difference. If you don't have electric lighting or minimal electricity to run hospitals, schools, basic communications, water pumps and treatment plants, ... then life is going to be difficult.
However, once you get to about 2000 kW hours per person per year, all the extra electricity beyond that makes little difference to basic human well being. This is frivolous use of air conditioners, aluminium smelters, conspicuous consumption, ...

Finally, we always need to distinguish correlation and causality. As people become more prosperous they do tend to consume more electricity. However, it is not necessarily the electricity consumption that is making them more prosperous. This is clearly seen by how flat the top of the curve is. Electricity consumption in Canada is almost four times that of Spain!

A more detailed discussion of the graph is in this book chapter by Vaclav Smil.

How do you find mental space?

I wish I knew. This is something I continue to struggle with.

To think clearly and creatively one needs to find "space" that is free from distractions and stresses.
I find it hard to believe that one can be really productive in the midst of noise, chaos, and multiple demands. I can't.

I know there are some individuals who are good at multi-tasking and even seem relish all the noise and hyper-activity. But, deep down I wonder if some are just "cranking the handle" and publishing the same paper again and again.

I contend that slow science is not just enjoyable but necessary.

Yet finding "mental space" is increasingly a problem because of fast pace of "modern" life. This is increased by greater demands for "productivity" and all the background noise from email, social media, and mobile phones.

So how does one find the necessary "mental space"?

I welcome suggestions.
Here are mine.

Turn off your email and/or phone.

Block out times for specific tasks. e.g. reading, thinking, writing, coding, and calculating.

Try and focus on one thing at a time.

Get organised.

Find "physical spaces" that are free from distractions.

Many mornings I work at home for the first few hours.
On the other hand, if you have young children at home, that is probably a bad idea!
Go to the library if that helps.
Sometimes I have done that when there was construction noise near my building.

Take a sabbatical.

Clear your desk (ugh!...)

What do you think?
I welcome suggestions.

A valuable new book on thermoelectricity

Kamran Behnia has published a book Fundamentals of Thermoelectricity

Such a monograph is overdue. I think the topic is particularly important and interesting for several reasons. (This is illustrated by the fact that I have written almost 40 blog posts on the topic).

• The thermoelectric power is a transport property that presents a number of rich and outstanding puzzles.
• The sign, magnitude, spatial anisotropy, and temperature dependence of the thermopower can put significant constraints on theories because the thermopower is so sensitive to particle-hole asymmetry. In comparison, often it may not be too hard to cook up a theory can get a resistivity that agrees with experiment. However, the thermopower is another story.
• Thermoelectric materials are technologically important. Furthermore, if someone can find a material with a "Figure of merit" that is just twice that of the best current materials we could throw out all our refrigerators with moving parts!

The book has a nice preface. Here are a few choice quotes.

To many readers of this book, it should be a surprise to learn that a consistent and unified theory for phonon drag is still missing.... 

Three chapters devoted to a survey of experimental facts aim to revive a number of forgotten puzzles...

But the embarrassment [discussed below] has vanished thanks for our forgetfulness and not to our cleverness....

Even more enigmatic than the positive Seebeck coefficient of noble metals at room temperature is their thermoelectric response at very low temperatures.... 

Before beginning to write this book, I did not know that there is an three-orders -of-magnitude gap between theory and experiment regarding the thermoelectric response of Bogoliubov quasi-particles of a superconductor....

Why such facts have gradually faded from the collective memory of the condensed matter physics community is another question that deserves to be raised but is not addressed by this book.

Section 6.5 "Origin of the Positive Seebeck Coefficient of Noble Metals"
begins with the following quote from Robinson in 1967.

For more than thirty years the absolute thermoelectric power of pure samples of monovalent metals has remained a nagging embarrassment to the theory of the ordinary electronic transport properties of solids. All familiar simple theory has promised us that in these materials the sign of the electron-diffusion contribution to the thermopower should be that of the charge carriers as determined by the Hall effect, i.e. negative; but instead it turns out to be positive for Cu, Ag, Au and—even more perversely—for Li alone of the solid alkalies. At least two generations of experimentalists have remained completely unshaken in testifying to these results as obstinate facts of life.

A great value of the book is that it brings together a diverse set of experimental data from a wide range of materials.

I have a few minor quibbles.

I could find no mention of:

a. the Kelvin formula and the associated nice treatment of it by Michael Peterson and Sriram Shastry.

b. Dynamical Mean-Field Theory (DMFT) and how it nicely describes the thermopower as there is a crossover with increasing temperature from a Fermi liquid to a bad metal.

c. experimental techniques. What are the challenges, problems and obstacles to accurate and reliable measurements?

The caption of Figure 8.5 claims that for an organic charge transfer salt kappa-(BEDT-TTF)2Cu(NCS)2 "The expectations of a tight-binding model is in good agreement with the experimental data". The text says this is a "rare achievement in the case of correlated metals".
However, this "agreement" requires an arbitrary and unjustified rescaling of all the band energies by a factor of about five! This data and the theoretical challenge it presents is discussed in detail here.

The book is written by an experimentalist. I learnt from the back cover that there is also a new book, Modern Theory of Thermoelectricity by Zlatic and Monnier. I am looking forward to reading that.

Kamran Behnia has done a great service to the community by writing the book. Thank you!

Density Functional Theory (DFT) is exact. It is never wrong.

Some readers might be surprised to hear me claim this since I often highlight the problems and errors associated with calculations involving DFT. The problem is density functional approximations not the underlying theory.

There are two key ideas associated with DFT.

1. A theorem.
The ground state energy of an interacting electron gas is the minimum value of a unique functional of the charge density n(r) in the system.
This is an exact result.

The problem is that to determine the exact density and energy one needs to know the "exchange-correlation" functional.

2. An approximation.
One can make a local density approximation (LDA) to the exchange-correlation functional so that the density is written in terms of a set of "orbitals" that are found by solving a set of self-consistent equations that have a mathematical structure similar to the Hartree-Fock equations for the same system.

These distinct ideas are respectively associated with two different papers, published 50 years ago. The first is by Hohenberg and Kohn. The second is by Kohn and Sham. 
Aside: The history and significance of these papers has been nicely summarised recently in a Physics Today article by Andrew Zangwill.

I think the community needs to be more precise when they talk about DFT.

Broadly speaking, some people in the chemistry community give me the impression that they think if they can just tweak the parameters in their favourite exchange correlational functional then they are going to be able to get agreement with experiment for everything.

In contrast, consider this paragraph from the introduction of a recent physics paper:

Density functional theory (DFT), in essence a sophisticated mean field treatment of electron-electron interactions, provides a very good approximation to the interacting electron problem, enabling the theoretical description from first principles of many properties of many compounds. However, DFT does not describe all electronic properties of all materials, and the cases where it fails can be taken to define the “strong correlation problem.”

Surely, it would be better to replace DFT here with DFA=Density Functional Approximations.

Aside: I should say that besides this paragraph I really like the paper and the authors.

The distinction I am making here was particularly stressed in a recent talk I heard by Tim Gould.

Should people get credit for papers that are influential but wrong?

A colleague once told me a story about his research field.

"Ten years ago Professor X got some surprising experimental results. He then made bold claims about what this meant. Some people did not believe it. But, people then did detailed experimental and theoretical work to test his results and claims. They basically found that he was wrong but in the process they made some valuable and interesting discoveries and clarified several issues in the field. To half the people in the field he was a hero and to the other half he was a pariah."

The hero status was assigned because if he did not exist or had not made these claims, the new discoveries would not have been made (or might have been made much later).
The pariah status was assigned because he did not do careful scientific work and misled people.

How much credit should people get who open up new scientific directions with “wrong” papers or with unsubstantiated speculation?

Different people I talk to have quite different views about this.

My view is that such people should get very little credit, particularly if their work is sloppy and/or they engage in hype, self-promotion, and unsubstantiated speculation. 

On balance, I think such individuals have a negative overall influence on science. This problem has been compounded by the speculative and hype culture enhanced by the rise of the luxury journals. Rewarding people for doing bad science is just going to promote more bad science. Maybe one in fifty bad papers will have fruitful consequences. But the other 49 will waste time and resources and create confusion.

What do you think?

Emergent quasi-particles and adiabatic (dis)continuity

In quantum many-body physics quasi-particles are emergent entities. But, it is worth making a distinction between two cases.

1. Adiabatic continuity.
As one gradually turns on the interactions the excited states of the system smoothly evolve from those in the non-interacting system. As a result the quasi-particles have the same quantum numbers and statistics as the constituent particles. The most prominent example is in Landau's Fermi liquid theory which describes elemental metals and liquid 3He.

2. Adiabatic discontinuity.
The  quasi-particles do NOT have the same quantum numbers and statistics as the constituent particles. One example, is magnons (spin waves) in a spin-1/2 Heisenberg antiferromagnet. They have spin one and act like bosons. In contrast, the constituent particles are localised electron that are fermions with spin-1/2. An even more dramatic example occurs in the fractional quantum Hall effect. The constituent particles are electrons with charge -e and obey Fermi-Dirac statistics. But, the quasi-particles have fractional charge and obey anyon statistics.

This was recently stressed by Brijesh Kumar after a talk I gave.

The distinction is interesting because if you use Berry's criteria for emergence [a singular asymptotic expansion] (which I do like) then only in the second case would you define the quasi-particles as emergent.

The figure above describing adiabatic continuity is from Piers Coleman.

A comparative appreciation of P.W. Anderson and Linus Pauling

Andrew Zangwill contacted me because he is working on scientific biography of Phil Anderson. I think this is overdue. I would argue that Phil is the greatest theoretical physicist of the second half of the twentieth century. I would argue this on similar grounds to why I think Linus Pauling was the greatest theoretical chemist of the first half of the twentieth century. Crucially, their scientific legacies have extended far beyond condensed matter physics and chemistry, respectively.

Specifically, Pauling did not just make essential contributions to our understanding of chemical bonding, x-ray crystallography, and quantum chemistry. His impact went far beyond chemistry. Francis Crick said Pauling was the "father of molecular biology." He proposed and elucidated alpha helices and beta sheets in proteins. Furthermore, he began the whole field of molecular medicine, by showing the molecular basis of a specific disease, sickle cell anemia.

Phil Anderson has made incredibly diverse and valuable contributions to condensed matter physics (anti-ferromagnetism, localisation, weak localisation, magnetic impurities in metals, Kondo problem, poor mans scaling, superfluid 3He, spin liquids, RVB theory of superconductivity... ).
I can think of three significant and profound influences of Phil beyond condensed matter physics.

Codifying and elucidating the concept of emergence (and the limitations of reductionism) in all of science, in More is Different in 1972.

Laying ground work for the Higgs boson in 1963 by connecting spontaneous gauge symmetry breaking and mass. 

Elucidating spin glasses in a way that was key to John Hopfield's development of a particular neural network and to the notion of a "rugged landscape", relevant in protein folding and evolution. Anderson described these connections nicely in two pages in Physics Today in 1990.

Are there other examples?

Who do you think is the greatest theoretical physicist of the second half of the twentieth century?
[n.b. If you are thinking Feynman, he did path integrals and QED before 1950].

All rankings should include error bars

In introductory science courses we try and instill in undergraduates the basic notion that any measurement has an error and you should estimate that error and report it with your measurement. Yet "Professors" who are in senior management don't do that.

Today in Australia the results of the Excellence in Research Australia (ERA) ranking exercise were announced. Every research field at every university is given a score. A colleague wisely pointed out that given the ad hoc procedure involved all the rankings should include error bars. He conjectured that the error bar was about one. Hence, one cannot distinguish the difference between a 4 and 5. Yet, this is a distinction that university managers and marketing departments make a lot off.

I think for almost all ranking exercises it would be quite straight forward for the compilers to calculate/estimate the uncertainty in their ranking. This is because almost all rankings are based on the average of rankings or scores produced by a number of assessors. One simply needs to report the standard deviation in those scores/rankings. I think the conclusion of this will be that rankings largely tell us what we knew already and that any movement up or down since the last ranking is within the error bars. John Quiggin has made such arguments in more detail.

The ERA is largely modelled on the UK equivalent; originally, called the RAE but now the REF. This has been widely criticised; it wastes massive amounts of time and money, involves flawed methodology, and has been devastating for staff morale. These issues are nicely (and depressingly) chronicled in a blog post by Liz Morrish. One academic Derek Sayer fought to be excluded from the RAE as a protest.  He explains in detail why it is such a flawed measure of real scholarship.

 It is also worth looking at The Metric Tide: Report of the Independent Review of the Role of Metrics in Research Assessment and Management, commissioned by The Higher Education Funding Council which is responsible for the REF. Reading the recommendations is strange. It sounds a bit like "most people think metrics are rubbish but we are going to use them anyway...".

What is omega/T scaling?

And why is it so elusive?

Quantum many-body systems are characterised by many different energy scales (e.g. Fermi energy, Debye frequency, superconducting energy gap, Kondo temperature, ....). However, in many systems properties are "universal" in that they are determined by a single energy scale. This means that the frequency (omega) and temperature (T) dependence of a spectral function can be written in a form such as

where here  T_ K is the relevant energy scale and I set hbar =1 and k_B = 1.

However, what happens in the limit where the relevant energy scale T_K goes to zero, for example near a quantum critical point? Then the only energy scale present is that defined by the temperature T and we now expect a functional dependence of the form

This is omega/T scaling.

In one dimension the form of the scaling function is specified by conformal field theory and for quantum impurity problems (e.g. Kondo) by boundary conformal field theory.

In 1989 Varma et al. showed that many of the anomalous properties of the metallic phase of the cuprate superconductors at optimal doping could be described in terms of a “marginal Fermi liquid” self energy. They associate this with a spin (and charge) fluctuation spectrum that exhibited omega/T scaling (for all wave vectors). Specifically, the spectral function was linear in frequency at low frequencies, up to a frequency of order T.

Some claims about quantum criticality in cuprates are debatable, as discussed here.

Finding concrete realistic theoretical microscopic fermion models that exhibit such scaling has proven challenging.

In his Quantum phase transitions book Sachdev reviews several spin models (e.g. transverse field Ising model in one dimension) that exhibit omega/T scaling in the quantum critical region, associated with a quantum critical point.

 In 1999 Parcollet and Georges  considered a particular limit of a random Heisenberg model which had a spin liquid ground state and a local spin susceptibility chi’’(omega) that exhibited a form consistent with that conjectured in the marginal Fermi liquid scenario.

Local quantum criticality has been observed in a few heavy fermion compounds.  Specifically, in 2000 Schroder et al. observed inelastic neutron scattering gives the following \omega/T scaling,

In 2008 Kirchner and Si showed that near the quantum critical point in the Ising-anisotropic Bose-Fermi Kondo model (BFKM) with a sub-ohmic bath (i.e. a very specific model!) they obtained omega/T scaling similar to that associated with boundary conformal field theory, even though the model has no obvious conformal invariance.

This is my potted history and understanding. I welcome corrections and clarifications.