Strongly correlated electron systems in high magnetic fields II

When and how can a large magnetic field change the ground state of a strongly correlated electron metal?

An earlier post considered this question.

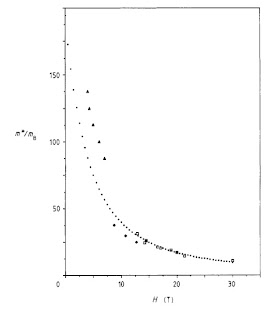
To me, one of the most striking cases is that of heavy fermion metals in high magnetic fields. From quantum magnetic oscillations [e.g., SdH and dHvA] one can measure the effective mass of the Fermi liquid quasi-particles. The figure below shows how in CeB6 the effective mass decreases significantly with increasing magnetic field. Hence, the field destroys the heavy fermion behaviour.

What is the physics behind this dramatic effect?
The heavy fermion character arises from the formation of Kondo singlets between the localised spins and the conduction electrons. However, an external magnetic field breaks these singlets, reducing the heavy fermion character. The Kondo lattice temperature [coherence temperature] sets the relevant magnetic field scale  and is well described by a slave boson theory of Wasserman, Springford, and Hewson [see eqn. 17 for m*(H)]. It also contains the above figure.

A more sophisticated treatment [connecting to recent NRG (Numerical Renormalisation Group) treatments of the single impurity Anderson model] of the case of YbRh2Si2 has recently been discussed by Zwicknagl. I am not clear on why she (and Hewson!) do not reference this earlier slave boson theory in their latest work.