How to win a Nobel prize with a mean-field theory

This week in the Quantum Many-Body Theory reading group we look at Chapter 6 of Advanced Solid State Physics by Philip Phillips, concerning local magnetic moments in metals and the Anderson model.

Here are my random notes.

The essential physics is captured by the Hartree-Fock solution.

The Coulomb repulsion (Hubbard U) leads to qualitatively different behaviour: the formation of local moments. This is embodied in the zero-temperature phase diagram.

I suspect that when Anderson published this diagram in 1961 this was a new way of looking at a quantum many-body problem.

It is all about competition between the three energy scales: U, the hybridisation energy, and the energy separation of the Fermi energy and the localised energy level.

Anderson shared the Nobel Prize in 1977 with Mott and Van Vleck. Anderson was cited for this work on local moments and localisation due to disorder.

The model and the associated physics has a relevance that goes far beyond the question of local moments in metals. It is at the heart of dynamical mean-field theory (DMFT) treatments of Hubbard models and electronic structure calculations that capture correlations better than DFT-based approaches.

The model also describes quantum dots in semiconductor heterostructures (which have tuneable Hamiltonian parameters) and chemisorption of atoms on metal surfaces (Anderson-Newns model).

Anderson's solution is actually "wrong"! At zero temperature the ground state is always a spin singlet. However, these singlets only form at low temperatures (below the Kondo temperature).

In the local moment regime the Anderson model reduces to the Kondo model (chapter 7).

The model turns out to be exactly soluble with the Bethe ansatz. This was shown by Tsvelick and Wiegmann in the early 80's. They showed that the ground state is always a singlet at zero temperature.

A passion for science

Glenn T. Seaborg was the father of heavy element chemistry. It is interesting how we was so driven by a passion for science and for educating the next generation. Even though he had a Nobel Prize (1951) and had been Chair of the Atomic Energy Commission (equivalent to Secretary of the Department of Energy today) in 1971 he returned to Berkeley to teach and to lead a research group.

In the National Academy Biographical Memoir by Darleane C. Hoffmann, who was his successor at Berkeley, says:

I learned so many things from him just by observing how he ran the weekly brown bag lunches with his graduate students and later mine--listening with great interest as they described their research progress. He asked insightful and penetrating questions, but not in a threatening manner, made suggestions, and frequently went to visit the labs late in the day to see what was going on. He also hosted many undergraduate research students. He was devoted to education and student training and would prepare as carefully for lectures to freshman chemistry classes as for presentations to prestigious assemblages of scientists.

This post was stimulated by a dinner discussion yesterday with a former group member who said something very similar. In particular, Seaborg was a stickler for keeping appointments with students. He would excuse himself from meetings with "big shots" to meet with students.

An equation you should know

Next month I am going to India to speak at a School and Conference on “Emergent Properties and Novel Behavior at the Nanoscale” organised by I2CAM and the Jawaharlal Nehru Centre for Advanced Scientific Research (JNCASR) in Bangalore.

In the school I will give a one hour long lecture. Here is the abstract I have submitted. Any feedback welcome. Some related material is discussed in this talk I gave last year in the Black Forest.

Quantum design principles for functional electronic materials

In a complex material how does one optimise the quantum efficiency of the transition

between two different quantum states when there are many alternative transitions available to a system?

Regardless of whether or not it is explicitly stated this is the question which is at the heart of a wide range of research. Prominent examples include understanding biomolecular function, designing organic photovoltaic cells, and catalysis.

I will discuss how this optimisation problem involves a subtle interplay between quantum coherence and decoherence induced by the system environment. The essential physics involved can be understood in terms of the spin-boson model which describes two quantum states which are coupled to one another with an environment which is modelled by a collection of an infinite number of harmonic oscillators.

Qualitatively different dynamics occurs depending on the relative magnitude of the key energy and time scales in the problem: the thermal energy, energy difference between the two states (epsilon), the coupling of the two states (and the associated Rabi frequency), the reorganisation energy of the environment, and the typical relaxation time of the environment.

Perhaps it is not appreciated enough that for most systems of interest all of these energy scales are well-characterised.

The incoherent "classical" regime of the spin-boson model gives a simple expression for the transition rate which is the same as the Marcus-Hush expression for the electron-transfer rate. I consider this is one of the most important equations in chemical physics and particularly for the understanding and design of functional materials.

I will discuss several important applications of this equation.

1) A design principle:

The rate is a maximum for a specific non-zero value of the coupling to the environment where epsilon equals the reorganisation energy.

2) The temperature dependence of the charge mobility in molecular materials.

[This is the same expression as given by small polaron theory].

3) Forster resonant energy transfer between chromophores.

Quantum dynamics of nuclear collisions

Today I was at the Department of Nuclear Physics at ANU with collaborators discussing quantum decoherence in heavy ion collisions.

Kouichi Hagino was visiting from Japan and gave us a nice overview of the coupled channels approach to nuclear collisions. He made use of some really nice lecture notes he gave at a summer school in 2006.

Quantum chemistry par excellence

Seth Olsen has a really nice paper that just appeared ASAP online in the Journal of Chemical Theory and Computation.

A real challenge of high-level quantum chemistry is to connect it to chemical concepts, chemical trends and semi-empirical theories. This seems to rarely happen. There is a tendency to just throw ones arms up in the air and say, "It is too hard! One just has to calculate the properties of every molecule from scratch."

However, Seth has shown how correlated quantum chemical calculations for an important class of methine dyes can illuminate, clarify, and provide justification for resonance theories of dye colour that go back to the forties, including from John R. Platt.

The figure below compares excitation energies calculated ab initio with those from a parametrisation of Platt's model.

It is well known that ....

I just read this advice:

1. Be an outsider. Don't be unduly awed by authority,...

2. Be fact driven. An obsession with facts can help you avoid common pitfalls and the bending of facts to fit your theories....

3. Respect the unknowable. Work on the assumption that too many people are too certain about the inherently uncertain things.

4. Always question your own convictions. Most of us look for verification of our own beliefs. Instead you should be open to having your ideas criticised. Only through this kind of stress testing can the true validity of your beliefs be determined.

5. Employ meta-cognition. Consciously practise all the steps above to avoid falling into overconfidence when success is experienced.

Actually, this advice is not about doing science. It is from Kathryn Schutz's reflections Five lessons for investors, from Michael Lewis's The Big Short. I read the above summary in The Week.

But, it seems to me it is good advice also for doing better science!

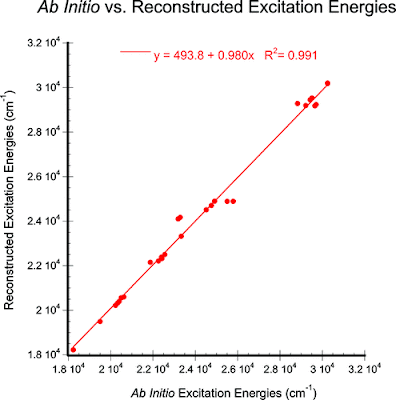
Deconstructing excitons in organic materials

Previously, I asked is organic semiconductors a misnomer?

One needs to be very careful about trying to apply the same concepts from inorganic semiconductors to organic materials used to make devices such as photovoltaic cells.

An important example is excitons.

In inorganic semiconductors these arise from the Coulomb interaction between an electron and a hole and that have binding energies of much less than an electron Volt and they have a spatial extent of many lattice constants. They are sometimes called Wannier-Mott excitons.

Because they are so large variation of the dielectric constant of the material has a significant effect on the binding energy and spatial extent. As a first approximation one solves the hydrogen atom problem with the band effective mass and material dielectric constant.

However, the excitons (i.e., low lying singlet excited states are produced by photon absorption and can decay radiatively) in organic materials are VERY different. They are usually spatially localised on a single molecule. They are sometimes called Frenkel excitons.

The localisation can be seen by making a dilute "solution" of the molecules in a glass or matrix. They differ little from a thin film of just the molecules. The binding energy (i.e., the energy difference between the excited state and that of an electron and a hole on two neighbouring molecules) can be of the order of an electron Volt and reflects electronic correlations on the molecule. Except in very clean single crystals, there are usually no bands (and so an effective mass cannot be defined) and the dielectric constant does not determine the binding energy or the spatial extent of the exciton.

A great quantum many-body theorist

Today is Ada Lovelace day [I thank Ben Powell for bringing this to my attention] and so I asked myself, "Which woman has made the greatest contribution to quantum many-body theory?"

Maria Goeppert-Mayer is best known for receiving the Nobel Prize in Physics for her role in developing the nuclear shell model.

However, she did more. In 1938, together with Sklar, she did one of the first non -empirical quantum chemistry calculations: the excited states of benzene. This is in a widely cited Journal of Chemical Physics paper.

Problems with Hartree-Fock

This weeks reading from Advanced Solid State Physics by Philip Phillips is Chapter 5, Interacting Electron Gas. Some key ideas:

The Hartee-Fock equations for the Jellium model [equations 5.4 to 5.6] have plane wave solutions. These correspond to quasi-particles and have the energy dispersion relation 5.1.

The exchange hole refers to the fact that electrons of like spin avoid one another due to the Pauli exclusion principle. This means the energy is less than the Coulomb repulsion energy of an electron moving in a uniform charge density.

The total energy of all the occupied Hartree-Fock states gives an "exchange energy" which only depends on the electron density (5.14). [This expression is sometimes used in the X_alpha method of Slater and the Local Density Approximation (LDA) of Density Functional Theory (DFT)].

The HF excitation spectrum is qualitatively incorrect. It predicts that the low-temperature specific heat of metals should go like T/ln(T) whereas it is always observed to go like T. This problem can be resolved by including screening, which cuts off the long-ranged Coulomb potential (see Chapter 8).

HF energy can be used to calculate the cohesive energy of simple metals. The result is worse than the non-interacting electron model! This difficulty arises because the direct and exchange Coulomb energies almost cancel each other.

The quasi-particles have lower energy than free particles because of the exchange hole.

Deconstructing Anderson's radical proposal?

In 1987 Anderson made the radical proposal concerning doping Mott insulators:

"The preexisting magnetic singlet pairs of the insulating state become charged superconducting pairs when the insulator is doped sufficiently strongly."

The material SrCu2(BO3)2 has been argued to be a Mott insulator on the Shastry-Sutherland lattice (see Figure below). In the corresponding Heisenberg model there is an exchange interaction J along all vertical and horizontal bonds and a diagonal interaction J' along every second plaquette. It can be shown that for J'/J > 1.44 +/- 0.02 that the exact ground state is a product of singlets along the diagonals.

Liu et al. studied the corresponding t-J model (including three site hopping terms) away from half-filling using a projected BCS wave function. They considered the model with t'=+/- 1.25 t and J=0.3t. They found the following (summarised in the Figure below).

(i) There is significant particle-hole asymmetry. This is because one sign of t' corresponds to electron doping and the other to hole doping while t does not change.

(ii) Hole doping produces d-wave superconductivity. But, this is NOT the result of delocalisation of the pre-existing singlets in the Mott insulator since they were along the diagonals.

(iii) Electron doping does not produce superconductivity, but only a correlated metal with singlet pairing along the diagonal, as in the parent Mott insulator.

(iv) The hole-doped superconducting state co-exists with plaquette bond order where all the nearest neighbour spins have antiferromagnetic correlations. Thus the spin correlations are qualitatively different from in the parent Mott insulator.

I feel this paper has not received the attention that it deserves. It shows that the competition between superconductivity and antiferromagnetism and resonating valenc bonds that occurs when doping a frustrated Mott insulator is more subtle (and confusing) than suggested by Anderson's original conjecture.

On the other hand, one might argue that the parent Mott insulator is very different from the cuprates and organics because there are NO resonating valence bonds in the parent insulator.

Aside: I am confused about (i). I thought that when one goes from particles to holes one changes the sign of both t and t'. But, is this difference because they include the three site hopping term in the t-J model?

Error bars please

When we teach undergraduates laboratory subjects we are always on the case of the students about using the appropriate number of significant figures and always quoting error bars. However, it seems the scientific community does not apply the same criteria to themselves when quoting and comparing quantities such:

• average scores on student evaluations of teaching
• impact factors of journals
• citation rates per paper

For example consider the graph below of impact factors of physical chemistry journals from 2001

This site reports "large changes" in impact factors of Chemistry Journals from 2007 to 2008. It reports that of ChemPhysChem changed from 3.502 to 3.636.

J. Phys. Chem. B changed from 4.086 to 4.189.

This suggests to me most of the comparisons are in the noise.

I would suggest that what we would tell our first year undergrads to do with data like this is something like:

"take the data from 5 years, average it and find the standard deviation. use the latter as your error."

This would lead to a conclusion something like, "the impact factor of J. Phys. Chem. B is 4.0 +/- 0.2 and of ChemPhysChem 3.7 +/- 0.3. this is consistent with the theory that these journals are of comparable quality...."

Futhermore, we would keep sending the students back to their lab books or marking them down until they did. So lets get rid of the double standard!

Geometric frustration of kinetic energy

Just as one can discuss geometrical frustration of spins in antiferromagnets one can also discuss geometrical frustration of the kinetic energy of electrons on similar lattices.

But it should also be noted that this is a strictly quantum mechanical effect arising from quantum interference. This is in distinct contrast to geometrical frustration in antiferromagnets which can occur for purely classical spins.

A few years ago, Jaime Merino, Ben Powell, and I discussed trying to quantify this kinetic energy frustration. (See Section IIC of this long PRB paper). In a non-interacting electron model the only proposal we were aware of for a quantitative measure of this frustration of the kinetic energy was due to Barford and Kim:

I am wondering if the width of the lowest lying band of triplet excitations may be a good measure of frustrations in a quantum antiferromagnet. More on that later...

Listen to the questions

When you give a talk, listen carefully to the questions.

Do not cut off the questioner, even if you think they are mistaken. Let them finish.

You can learn a lot from the questions and criticism and skepticism of your audience, even if you disagree.

Answering, "I don't know. I will try and find an answer for you" is preferable to waffling on about things you do not understand or making claims you cannot back up. The latter reduces your credibility considerably more than the former.

Caveat: it is easier to give advice than to actually put it into practice. Like all advice I give here I do not claim that I always do it myself. But, it is what I want to aim for.

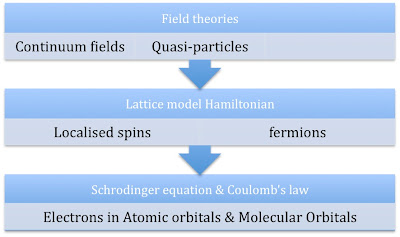
Emergence of a hierarchy

The hierarchy of objects and descriptions associated with theories of electronic properties of solids.

[n.b. the arrows should point up not down! I am graphically challenged]

At the level of quantum chemistry one can describe the electronic states of single (and pairs of) molecules in terms of molecular orbitals which are linear combinations of atomic orbitals. [This is Laughlin and Pines, Theory of Everything!]

Just a few of these orbitals interact significantly with neigbouring units in the solid. Low-lying electronic states can be described in terms of itinerant fermions on a lattice and an effective Hamiltonian such as a Hubbard model. In the Mott insulating phase the electrons are localised on single lattice sites and can described by a Heisenberg spin model. The low-lying excitations of these lattice Hamiltonians may have a natural description in terms of quasi-particles which can be described by a continuum field theory such as a non-linear sigma model.

A good place to start a many-body theory

Last week I briefly discussed the notion of quasi-particle weight and recommended P.W. Anderson, Concepts in Solids: Lectures on the Theory of Solids, Chapter 3.

This week we looked at Chapter 4, in Advanced Solid State Physics, The Hartree-Fock approximation.

This is can be viewed as a mean-field theory and/or a variational approximation to the ground state energy. One assumes many-particle ground state wavefunction can be written as a single Slater determinant.

One way to understand the Hartree-Fock equations (4.23) as a mean-field theory is the following. Consider the Coulomb interaction energy between an electron in one orbital (denoted nu) [which has an associated charge density] and the charge density associated with all the other occupied orbitals.

The one electron energies are actually the Lagrange multipliers introduced to care of the normalisation constrain for the one electron orbital wave functions.

The exchange interaction (between electrons in different orbitals) arises because of the fermion statistics. It leads to a splitting of singlet and triplet states. The latter has lower energy because the electrons are forced to occupy different spatial regions by the Pauli exclusion principle.

Hartree-Fock theory is the starting point for almost any attempt at solving a quantum many-body problem.

In Chapter 6, we will see how Anderson used it to solve the problem of local magnetic moments in metals, work recognized in the 1977 Nobel Prize in Physics.

If you want to solve the Hartree-Fock equations for a few simple molecules try WebMO

Want ad: a measure for quantum frustration

In the latest issue of Nature, Leon Balents has a nice comprehensive review article, Spin liquids in Frustrated Magnets.

In a Box at the side Leon considers the problem of quantifying the amount of frustration in an antiferromagnetic material (or model) and considers a measure (emphasized by Ramirez in a classic review) f=T_CW/T_N, the ratio of the Curie-Weiss temperature to the Neel temperature, at which three-di

mensional ordering occurs.

Although, indicative of frustration I think we should come up with a more precise measure. One limitation of this measure is it does not separate out the effects of fluctuations (both quantum and thermal), dimensionality, and frustration. For strictly one or two dimensional systems, T_N is zero. For quasi-two-dimensional systems the interlayer coupling determines T_N. Thus, f would be larger for a set of weakly coupled unfrustrated chains than for a layered triangular lattice in which the layers are moderately coupled together.

In 2005, Weihong Zheng, Rajiv Singh, Radu Coldea, and I published a paper, Temperature dependence of the magnetic susceptibility for triangular-lattice antiferromagnets with spatially anisotropic exchange constants.

In Section II we discuss in some detail two different measures of frustration for model Hamiltonians:

1. the number of degenerate ground states

2. the ratio of the ground state energy to the

base energy defined by Lacorre.

The base energy is the sum of all bond energies if they are independently fully satisfied.

One of the main results of our paper is the Figure below

All of the quantities plotted are meaurable in an actual material.

In some sense then the temperature Tp at which the susceptibility has a maximum and the magnitude of that susceptibility is a measure of the amount of frustration. This is consistent with our intuitive notion (prejudice, bias?) that the largest frustration occurs for the isotropic triangular lattice (J1=J2).

These measures of frustration are not dependent on dimensionality and so do not have the same problems discussed above that the ratio f does.

But, it is not clear to me that these measures distinguish quantum and classical frustration. Surely there is a difference? Could entanglement measures help?

Trends in organometallic complexes

As a physicist trying to understand what makes a good organic LED material it is easy to get lost in all the chemical details. Today I came across a review, Light-emitting iridium complexes with tridentate ligands, by W^3 (Williams, Wilkinson, and Whittle!) which has the cute and useful abstract picture below

If you wade through the paper Figure 17 (below) suggests how to understand differences between different ligands in terms of frontier orbitals. They also discuss how the character of the emitting triplet state changes for the different complexes.

How wrong about the future can you be? III

I now discuss a second of the four articles I introduced in an earlier post.

This article is one I know that Phil Anderson likes to rant about.

Brian Pippard, The Cat and the Cream, 1961.

A banquet speech given at a conference on superconductivity held at IBM's new lab at Yorktown Heights, and later published in Physics Today.

Here are a few choice quotes:

the era of the great breakthrough is over..... I have found that when I suggest to senior physicists that the end of physics as we know it is in sight, they tell me, "That's just what everybody was saying in 1900". Now this may be a justification for optimism, but let's first ask whether the historical parallel is sound. I think in many ways it is.

....If you don't believe me, ask yourselves this question: Apart from the field of fundamental particles, what is the most recent discovery in physics that still remains in essence a mystery? I think I might remark that in low-temperature physics the disappearance of liquid helium, superconductivity, and magneto-resistance from the list of major unsolved problems has left this branch of research looking pretty sick from the point of view of any young innocent who thinks he's going to break new ground.

....but with the new IBM Laboratory, and all those other labs that we represent, plugging along assiduously doing research, ten years is going to see the end of our games as pure physicists,....

Note, that the same time Pippard was giving this talk his very own Ph.D student, Brian Josephson was making a discovery that led to elucidation of spontaneously broken symmetry, macroscopic quantum tunneling, superconducting qubits, .....

Galaxy formation as a condensation phenomena

Yesterday there was an interesting colloquium, Simulating star cluster evolution on high-end graphics cards, by a new UQ staff member, Holger Baumgardt.

The fact I am writing a blog post about it should be taken as a compliment and the comments below need to be taken with a large grain of salt, since the subject goes way beyond my expertise. But they may be interesting in terms of how an outsider sees things...

First, a few things I learnt.

Globular clusters are 10-12 billion years old, much older than typical galaxies.

Black holes may be at the centre of most galaxies.

UCDs are ultra-compact dwarf galaxies somewhere between star clusters and galaxies.

The figure below shows a plot of the radii of different objects versus their mass. It is taken from this paper.

Scaling relations for low-mass, hot stellar systems: half-light radius plotted against total mass.The dashed line shows the fitted relation for elliptical galaxies, while the solid lines indicates the median for Galactic globular clusters ( pc) that do not follow a mass-radius relation.

The claim appears to be that there is a qualitatively different behaviour between galaxies (thousands of stars) and globular clusters (millions of stars).

Ben Powell asked an important question: does the data shown in the talk (similar to that above) justify this claim?

It is not clear to me that it does.

If there is a qualitative change when one has more than a million solar masses, than an important theoretical question to answer is why?

A challenge to computer simulations is to then try and reproduce this change. On a regular PC one can simulate the classical dynamics of thousands of stars. But what about a million? Hence, the desire to use graphics cards...

A couple of questions I had (as an ignorant condensed matter physicist):

What happens if one attacks this problem in the continuum limit? (i.e., rather than having a million point like particles one has a continuous mass distribution).

Can one write down a "density functional" type theory?

Are there any analogies to other problems concerning condensation of liquid droplets whether in nuclear physics or low density gases?

Alan Mark asked a good question about the dependence of the simulation results on the choice of initial configuration. No doubt inspired by his experience with molecular dynamic simulations of large biomolecular systems, where I believe this can be problematic.

One of my scientific heroes: John R. Platt (1918-1992)

John R. Platt has featured on this blog before because of his paper in Science about "Strong Inference" and the "method of multiple alternative hypotheses". This stimulated my New Year's resolution.

Platt also wrote a really nice theory paper about organic dyes that will feature soon because Seth Olsen has a paper about to appear in Journal of Chemical Theory and Computation which gives a rigorous quantum chemical basis for Platt's theory.

I was wondering what happened to Platt and found an interesting 1992 Obituary in the New York Times.

I also found that Platt was on a panel discussion with Michael Polanyi about the interplay of reductionism and emergence in biology, physics, and chemistry.

To commute or not to commute

This weeks reading from Advanced Solid State Physics by Philip Phillips is Chapter 3, Second Quantization. Some key ideas:

Quasi-particles in quantum many-body theory are either fermions or bosons. The difference is seen in whether their creation and annihilation operators obey anti-commutation or commutation relations.

The second quantisation formalism provides a convenient and powerful book-keeping device to keep track of the fermionic (or bosonic) character of many-particle states.

A key result to become familiar with is writing a many-body Hamiltonian operator in second-quantised form, as in equation (3.33).

This is the starting point of Chapter 4, The Hartree-Fock approximation.

In the next chapter we will see how the anti-symmetric (fermionic) character of many-electron quantum states has an important physical consequence: the exchange interaction which leads to an energy splitting of singlet and triplet excited states. [A clear discussion of this is in Chapter 18, The Helium Atom, in Quantum Physics by Stephen Gasciorowicz.]

An alternative hypothesis for the cuprates

In Mike Norman's nice review of the theory of superconductivity in the cuprates he states:

The RVB spin gap was probably the first prediction for the subsequently observed pseudogap phase. In RVB theory, the pseudogap phase corresponds to a spin singlet state (with its resulting spin gap) but no phase coherence in the charge degrees of freedom. One of the interesting ideas to emerge from this was an explanation for transport in this phase, which reveals a metallic behavior for in-plane conduction, but an insulating behavior for conduction between the planes. In the RVB picture, the metallic behavior is due to the fact that the holons can freely propagate. But to tunnel between the planes, the holons and spinons must recombine to form physical electrons, and this costs the spin gap energy, thus one obtains insulating like behavior for the c-axis conduction (Lee, Nagaosa, Wen, 2006). This “gap” has now been directly seen in c-axis infrared conductivity data (Homes et al., 1993).

However, it seems to me that there is now an alternative hypothesis to explain the c-axis infrared conductivity data, which does not require this exotic recombination of holons and spinons into an electron. This is provided by a paper by Michel Ferrero, Olivier Parcollet, Gabriel Kotliar, and Antoine Georges, discussed in this earlier post. The difference between in plane and interplane transport arises simply from the wavevector dependence of the interplane hopping matrix element. But, the observed gap is still due to the pseudogap.

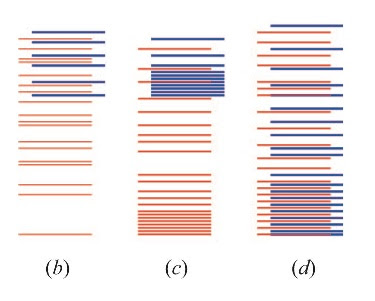
Excitation spectra of spin liquids and superconductors

I have been reading through Bruce Normand's review article, Frontiers in frustrated magnetism article in Contemporary Physics.

The focus is on spin liquids: how to define them and whether they exist in real materials and/or whether they are the ground state of physically reasonable quantum lattice Hamiltonians.

Bruce considers three different classes of spin liquids, each being defined by their excitation spectrum. In the figure below, singlets are red and triplets are blue.

(b) Type I. There is gap between the singlet ground state and both the lowest-lying triplet state and the first excited singlet state.

(c) Type II. There is gap between the singlet ground state and the lowest-lying triplet state. There is no gap to a continuum of low-lying singlet states.

(d) Algebraic spin liquids. There is no gap to either the lowest-lying triplet state or the first excited singlet state.

An important question is how to distinguish these different states experimentally. One basic question I am not clear on is: what are the qualitative differences between the dynamical spin susceptibility for the three different classes of spin liquids? This susceptibility is the quantity which determines inelastic neutron scattering cross sections and the NMR relaxation rate.

I believe singlet excitations do not contribute to the susceptibility but cannot find a proof of this. [Maybe work in the spectral representation and show that the relevant matrix elements between the singlet ground state and a singlet excited state must be zero?]

All these excitations will contribute to the specific heat capacity at low temperatures and the thermal conductivity. The singlet spectrum will not shift in a magnetic field but the triplets will split and the corresponding spectral weight be redistributed.

An what does this have to do with superconductivity? Well,.. strong coupling RVB-type theories focus on singlet excitations whereas weak-coupling AFM fluctuation theories focus on triplet excitations. This important point is nicely emphasized and discussed in this review on the cuprates by Mike Norman.

Sharing our ignorance...

I liked this xkcd cartoon since so many seem to feel they are well qualified to pass judgement on the evidence for and against climate change, biological evolution, big bang cosmology, consciousness, Schrodingers cat...

I thank Nathan Campbell for bringing it to my attention.

The future of quantum computing back then

This is the first post about one of the four articles mentioned in

How wrong about the future can you be?

Serge Haroche and Jean-Michel Raimond, Quantum Computing: Dream or Nightmare? Physics Today, 1996.

Actually, I think these authors were essentially correct 14 years ago when they concluded:

Even if quantum computing remains a dream, the physics of quantum information processing at the level of a few qubits is fascinating. Experiments on entangled particles with ions in a trap or atoms in a cavity will help us understand the fundamental aspects of quantum measurement theory, and they may lead to major improvements in the precision spectroscopy of simple quantum systems.

.... Testing quantum decoherence in conceptually simple experiments is also an important and challenging task. Rather than teaching us how to build a large quantum computer, such experiments are more likely to teach us about the processes that would ultimately make the undertaking fail. It is important to advertise this fascinating subfield of quantum optics for what, it really promises, which is a deeper insight into the most counterintuitive theory yet discovered by physicists.

Tips on writing papers

Fritz Schaefer is one of world's leading computational chemists. It is interesting read his list of minimum requirements for a first draft of a paper from his group. Two things to note:

• the emphasis that computational chemistry should be motivated by and ultimately connect with experiment
• the figures are key

Quantifying electronic correlations in simple metals

Considering natural orbitals in quantum chemistry this week reminded me of a key property of Fermi liquids: the existence of a discontinuity in the wavevector dependence of the Fourier transform of the one-electron reduced density matrix n(k).

The figure below is taken from a PRB paper by Paola Gori-Giorgi and Paul Ziesche. It shows the wavevector dependence of n(k) for a uniform electron liquid (at density corresponding to an interparticle spacing of rs=5, comparable to a typical metal). k=1 corresponds to the Fermi wavevector.

For a non-interacting fermion system n(k)=1 for k less than 1 and 0 for k >1.

The figure below shows the magnitude of zF, the jump in n(k) at k=1, as a function of rs. Increasing rs corresponds to decreasing electron density and increasing correlation effects. This quantity zF can be related to the quasi-particle weight associated with the pole in the one-electron Greens function. The smaller zF the larger the effective mass of the quasi-particles.

In a few weeks we will be looking at all this in the Quantum Many-Body Theory reading group.

How wrong about the future can you be?

Distinguished scientists trying to predict the future direction of a field of study is a dangerous (but fascinating) exercise. I have on my desk four such articles. I hope to comment on each in turn, but it is interesting to compare them since they are all very different, have had different impacts, and in hindsight some were pre-scient and others off track. Here they are in chronological order:

Niels Bohr, Light and Life, given at the International Congress of Light Therapy in 1932, and published in two parts in Nature in 1933 (Part 1 and Part 2).

Charles Coulson, Present State of Molecular Structure Calculations,

Given as an "after-dinner" speech at a quantum chemistry conference in 1959.

Brian Pippard, The Cat and the Cream, 1961

A conference banquet speech at a conference held at IBMs new lab at Yorktown Heights, and later published in Physics Today.

Serge Haroche and Jean-Michel Raimond, Quantum Computing: Dream or Nightmare? Physics Today, 1996.

Entanglement in quantum chemistry

Today I gave a talk at the weekly UQ Condensed Matter Theory group meeting (cake meeting because someone always brings a cake!) on the possible role of entanglement measures in quantum chemistry. I only got through the first half of these notes and so will continue next week.

Any comments welcome.

Quick to save the planet

A fundamental question concerning dye-sensitized solar cells is what determines the speed and efficiency with which charge is injected from the dye to the semiconductor (such as titanium oxide) on which it is absorbed?

A nice review by Liu and Andersen contains the summary diagram.

One important point I learnt is that (at least in some dyes) the ultrafast injection (~tens fsec) from the singlet excited state of the organometallic dye complex (such as those shown above) competes with intersystem crossing to the triplet excited state, from which injection can also occur but not as quickly.

Simplifying the Theory of Everything

This weeks reading from Advanced Solid State Physics by Philip Phillips is Chapter 2, The Born-Oppenheimer [BO] Approximation.

This reflects a key idea in quantum many-body theory: when there is a clear separation of energy scales one can often simplify the theory greatly and identify distinct quasi-particles [e.g., phonons and electronic quasi-particles] corresponding to the different energy scales.

Without BO there would be no quantum chemistry and no quantum theory of electronic properties of crystals.

BO is a consequence of the fact that electrons are much lighter than nuclei. Consequently, electrons in a molecule or solid have average velocities that are typically orders of magnitude faster than the nuclei.

Equation (2.1) is the Hamiltonian

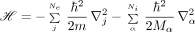
The symbols Zα and Mα are the atomic number and mass of the α^th nucleus, Rα is the location of this nucleus, e and m are the electron charge and mass, r _j is the location of the j ^th electron, and ℏ is Planck's constant.

If we could solve this Hamiltonian we would have Laughlin and Pines Theory of Everything.

Equations (2.10) and (2.14) are the key results of the chapter.

But there are many interesting and important situations where BO breaks down. Cases for molecules are discussed here.

Anderson's radical idea

In a 1987 Science paper Phil Anderson made a radical proposal, stimulated by the discovery of high-Tc superconductivity in layered copper oxides. [A meausure of the influence of Anderson's paper is that it has been cited more than 4000 times]. My version of Anderson's proposal is:

The fluctuating spin singlet pairs [produced by the exchange interaction] in the [Mott] insulating state become charged superconducting pairs when the insulating state is destroyed by doping, frustration or reduced correlations.

These fluctuations are enhanced by spin frustration and low dimensionality.

To me the idea is radical and rather counter-intuitive because in one sense insulating and superconducting states are so different. One has infinite conductivity and the other zero.

Ben Powell and I have been invited to write a review article for Reports in Progress in Physics concerning organic charge transfer salts which can be described by a Hubbard model on the anisotropic triangular lattice. [An earlier review of related materials is here].

A key issue is whether these materials can be used as tuneable systems to test ideas about the interplay of superconductivity, Mott insulation, quantum fluctuations and spin frustration.

A cautionary word about email

I was going to write a post about email and then remembered I wrote a post Think twice before you send that email in the early days of this blog. It says much of what I wanted to say again.

Think twice (or cool off) before you hit Reply or Send or Forward.

It is also worth reading some of the lists of "email etiquette" on the web. Here is one that I thought was pretty could.

Some of this may seem obvious and common sense. But to quote Steven Covey, "Common sense is not necessarily common practice."