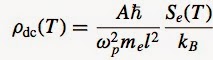Can you imagine a university president like this?

He gives away his whole salary to a not-for-profit.
He is reluctant to go into administration because he has to give up teaching.
He serves as president at the same institution for 35 years.
He increases the endowment from $9 million to $350 million.
When he takes over the university is mostly known for football. When he leaves it is a major research university.
He does not embrace the football program.
He introduces enrolment of female students.
He stands up to the president of the country over civil rights.
He is a major leader of campus opposition to a controversial war.
He changes the governance of the university so that it is no longer controlled by the sectarian founders, although he is one of them.
He speaks out often about issues of justice, human rights, racism, and poverty.
A survey of his peers identify him as the most effective college president in the country.

Is this fantasy? Could such a person actually exist?
Previously I posted about a dream graduation speech.
But, this president is real.

Theodore Hesburgh, President of Notre Dame University in the USA, from 1952-1987.
He died last week, aged 97.
The New York Times obituary is worth reading.

In praise of modest goals

Maybe it is just my personality but I increasingly find that in science and life I am out of step with the surrounding culture. I just have modest goals.  I just want to understand a few things and make some sort of reliable contribution. This means publishing in PRB, J. Chem. Phys., and occasionally in PRL. I don't aspire to publish in luxury journals, double my funding, to see my university the most highly "ranked" in Australia, or claim that my research will revolutionise materials science and molecular biology, ...
This is why I increasingly find it hard and tedious to write grant applications.
I will also be happy if Liverpool just finish in the top 4 of the Premier League....

I think good science is really hard and most advances come from long term projects with painstaking hard work and from the occasional serendipity.

Yet it seems society is sold on hype, the winner takes all mentality, and everyone should aspire to be a winner...

I am certainly interested in big questions and grand challenges. But I feel I am realistic about what contributions I and others (even the extremely gifted and well funded) can make. It is generally the long slow road. Earlier I posted about how I am skeptical and left cold by "big hairy audacious goals".

Here are a few of my inter-related problems with many of the goals and ambitions I encounter.

1. Many I find simply unrealistic, either scientifically, politically, or economically.
Furthermore, when I look at the ambitious goals that were hyped 5, 10, 20, and 30 years ago I see they have failed.

2. Many, particularly young, people are left feeling like "failures" because they did not "succeed" by becoming the "best", e.g. by publishing in a luxury journal.

3. They divert resources (time, energy, money, and talent) away from modest goals that may produce more actual fruit in the long term.
I think MOOC's, topological insulators, string theory, AdS-CFT, topological quantum computing, iron-based superconductors .... are all interesting and worth a few select groups playing around with. But I fail to see the justification for hordes of people working on them.

4. They can easily degenerate into fantasy and hype.

5. Some of these ambitious enterprises become institutionalised to the point that defending the "vision" leads to propaganda and an unwillingness to listen to criticism and change course. Peter Woit's blog does a nice job of showing how this is the case for string theory. Here are two other examples, from social activism.
Teach for America has the laudable goal of attracting gifted and privileged graduates to teach in poorly resourced schools. However, an article documents the incredible lengths they go to in order to mute negative publicity.
Microfinance is a great initiative that helps alleviate poverty in the Majority world. However, when two MIT economists, the authors of Poor Economics, did a systematic study of its effects, they found that it produced modest but tangible benefits. Unfortunately, they were roundly attacked by some not-for-profits because the study contradicted their grand claims that microfinance was completely transforming the lives of recipients.

But, maybe it is just my personality ...

Addendum: Reflecting on this more and starting teaching last week I realised that having modest goals for teaching and for seminars is also relevant. As one gets more experienced one realises just how little students (and seminar audiences) actually learn and understand. Hence, although I teach at a "high level" I try to make sure really basic points and skills are hammered home. Similarly, David Mermin's goal for a colloquium is modest.

The beauty and mysteries of imaginary time and temperature

Yesterday, at UQ Robert Mann gave a nice Quantum Science seminar, "Hot and Cold Accelerating Detectors".

It concerned the Unruh effect: suppose one observer is constantly accelerating relative to another. Then, what is a quantum vacuum (for a free boson or fermion field) to one observer is a thermally populated state to the other.

Specifically, if one considers a field with wave vector k and energy Ω k. Then the expectation of the number operator is,
$$\begin{array}{}\text{(5)}& ⟨<!--\; ⟨\; -->0|b_k^{†<!--\; †\; -->}{b}_k|0⟩<!--\; ⟩\; -->=(e^{2\mathrm{\pi <!--\; \pi \; -->}{\mathrm{\Omega <!--\; \Omega \; -->}}_k/g}-<!--\; -\; -->1{)}^{-<!--\; -\; -->1},\end{array}$$
which corresponds to a Bose distribution with a temperature given by
$$\begin{array}{}& T_{\mathrm{U}\mathrm{n}\mathrm{r}\mathrm{u}\mathrm{h}}=\frac{g}{2\mathrm{\pi <!--\; \pi \; -->}}=\frac{\mathrm{\hslash <!--\; \hslash \; -->}g}{2\mathrm{\pi <!--\; \pi \; -->}c{k}_B}\end{array}$$
where g is the constant acceleration. Note that this formula involves relativity (c), quantum physics (hbar), and statistical mechanics (kB).

I feel there is something rather profound going on here.
Without doing the calculation, it is perhaps not totally surprising that the accelerated observer sees a non-trivial occupation of excited states of the quantum field.
However, what is rather surprising to me is that the state occupation numbers has to be that associated with thermodynamic equilibrium.   Why not some other distribution? And that this holds for both fermions and bosons.
After all, you are starting purely with relativity [and the mathematics of Rindler co-ordinates] and quantum field theory and you are ending up with quantum statistical mechanics.
Is the thermal distribution just a "mathematical accident" because cosh functions are appearing in the Rindler co-ordinates, Bogoliubov transformation of the quantum field, and in thermal distribution?

The Scholarpedia page is helpful, stating this
``can also be understood as a manifestation of the general relationship between temperature and imaginary time in quantum statistical mechanics (KMS theory). When t and τ are extended as complex variables, iτ is revealed as an angular variable in the (it,z) plane. The periodicity determined by g, the acceleration, is the only one that makes functions of τ be analytic in t. That period corresponds, under the KMS theory, to the reciprocal of the Unruh temperature (Dowker, 1978; Christensen and Duff, 1978; Sewell, 1982; Bell et al., 1985; Fulling and Ruijsenaars, 1987).''

I welcome any further elucidations on this rich and subtle issue.

Convincing correlations

Given the complexity of human subjects in economics, sociology, and medicine it is hard to find data that clearly indicates a correlation between two variables. I read The Economist each week and many of the graphs that they present just look like random noise to me. However, a year ago they showed the curves below, that I found rather convincing.

The graphs are in an article Tobacco and health: Where there's smoke that marked the fiftieth anniversary of the USA Surgeon Generals report which contained the graph on the left showing a correlation between life expectancy and smoking. The graph on the right shows how cigarette consumption in the USA has changed over time, reaching a maximum around the time of the report and decreasing after the banning of broadcast advertising.

Unfortunately, the response of tobacco companies to their reduces markets in affluent countries has been to shamelessly promote smoking in the Majority World and to intimidate those who oppose them. This humorous/disturbing video from John Oliver describes their antics. I was very proud to see that the previous Australian government led the way in standing up to the companies.

What does the Hubbard model miss?

How is a Hubbard model related to Density Functional Theory?

Jure Kokalj and I recently wrote a paper where considered the effect of strong correlations on thermal expansion, all within the framework of a Hubbard model. This is mostly concerned with explaining anomalies in organic charge transfer salts at temperatures less than 100 K, i.e. much less than the Fermi energy.

One referee stated

“However conceptually this Hamiltonian can not capture the free energy of the relevant electrons loyally. Recall the total energy decomposition in density functional theory, the Hamiltonian corresponds only to the band energy part (which is a summation of occupied Khon-Sham states and different from the kinetic energy) plus interaction term. And the remaining Hartree part, exchange-correlated part and also ionic part, which depend on the lattice constants, are totally ignored. It is not known whether the contributions from such terms are trivial or monotonic especially when strong correlation is present. The neglect of such terms in the electronic model in use is not justified. In this sense, even though the parameters are taken from first principles estimations, it is not surprising that the results are not consistent with experimental data quantitatively and sometimes even qualitatively."

There are some subtle issues here that I would like to understand.
I am not sure I fully understand the referee's comments.
And, I am not sure I agree.

1. Do I understand that the referee is suggesting that the Hubbard model does not include the effects contained in the Hartree and exchange correlation term? Surely, this is not correct.

2. I agree that the Hubbard model will be missing all effects associated with core electrons and ionic terms. However, surely any effects associated with these will not vary significantly on energy and temperature scales of the order of 100 K?

I welcome any comments and insight.

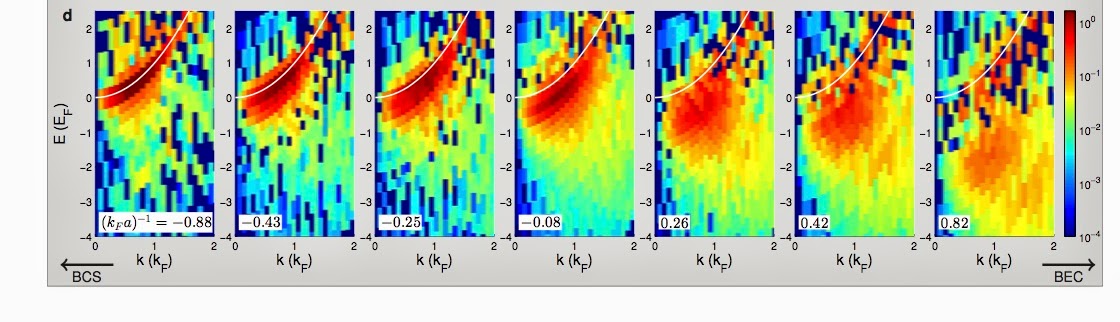
Mapping quasi-particles in strongly interacting ultra cold fermionic gases

There is an interesting preprint
Breakdown of Fermi liquid description for strongly interacting fermions 
Yoav Sagi, Tara E. Drake, Rabin Paudel, Roman Chapurin, Deborah S. Jin

It describes some nice ultra cold atom experiments that tune through the BEC-BCS crossover with a Feshbach resonance, focusing on the properties of the normal (i.e. non-superfluid) phase. All the measurements are at a temperature of T=0.2T_F, just above the superfluid transition.
It is like an ARPES [Angle Resolved PhotoEmission Spectroscopy] experiment in the solid state.
Specifically, the one-fermion spectral function A(k,E) is measured, shown in the colour intensity plots below.

The left and right side correspond to the BCS and BEC limits respectively. The unitary limit [i.e. infinite interaction occurs close to the middle].

On the left one can clearly see dispersing quasi-particle excitations, as one would expect in a Fermi liquid. As the interaction strength increases this feature is broader and there is more incoherent spectral weight at lower energies.

Some caution is in order as there is quite a bit of curve fitting involved in the analysis of the above data. [Solid state ARPES also suffers from this problem to.]

Specifically, the form below is used for the spectral function, where Z is the quasi-particle weight

In an earlier post I considered the history of this type of expression.

For the incoherent part the authors make the somewhat ad hoc assumption that it is given by a
 "function that describes the normal state in the BEC limit, namely, a thermal gas of pairs."

They then find the following results for the dependence of Z and the effective mass m* [defined by the quadratic dispersion] on the interaction strength [a is the scattering length, which becomes infinite at the Feshbach resonance, i.e. for the unitary limit].

There is already a theory paper that discusses the experiments. It captures the results above at the semi-quantitative level using a Brueckner-Goldstone theory. The self energy is assumed to be frequency independent in this approximation. I found this interesting as it is the opposite to Dynamical Mean-Field Theory (DMFT) for which the self energy is assumed to be momentum independent.

I feel the paper title may be a misnomer. The quasi-particle weight is always finite, except in the BEC regime [attractive interactions] where one does not really have fermions anymore.

In future experiments, it would be nice to see the temperature dependence of the spectral function. Specifically, do the quasi-particles get destroyed with increasing temperature as in bad metals.

I thank Matt Davis for bringing the preprint to my attention.

The case against citation metrics

This year I am on a committee that looks at funding applications from all areas of science. Inevitably, this will lead to problematic comparisons of the track records of mathematicians versus physicists versus biologists. The quick, lazy, and unjustified recourse is to start invoking impact factors and publications in luxury journals.

There is a very thorough and helpful report Citation Statistics from the International Mathematical Union that clearly shows how problematic citation metrics are.
Of particular interest is the graph below.

Note that mathematicians are cited three times less than physicists and six times less than life scientists.

Aside: I am not clear what the distinction is between life sciences and biological sciences. Is the latter more oriented to humans [e.g. medicine] and the latter plants and animals?

This report is cited in the San Francisco Declaration on Research Assessment, initiated by biologists, that is attracting significant interest and mentioned by Carl Caves on High Impact Factor Syndrome.

For profit universities are problematic

One of the most crazy and disturbing ideas of the current Australian government for "reform" of universities is to "become more like the USA" which means to "deregulate", "make users pay" and "increase competition" and allow more "private [i.e. for profit] providers". This video by the inimitable John Oliver shows why for-profit colleges [coupled with generous government loan schemes] are a really bad idea.



A less entertaining but thorough analysis of the Australian proposals, and with similar concerns, has been given by my UQ economics colleague Paul Frijters on the Core Economics blog. 

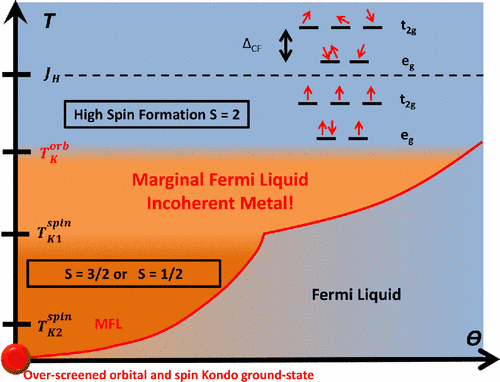
Rich Kondo physics in iron-based superconductors.

One of the most fascinating, challenging, and frustrating aspects of the iron-based superconductors is the presence of many competing energy scales, particularly associated with Hund's rule coupling.
There are debates about just how strong the correlations are, how large the spin moments are, and how relevant Mott physics is.

Furthermore, Hund's rule seems to lead to an unusual metallic state that is both difficult to characterise and describe theoretically. It has some signatures of a bad metal, as emphasised by (amongst others) Haule, Kotliar, Si, and Abrahams, but this characterisation is disputed by Johnston in his review [see Section 3.8.2].

Given the chemical and structural diversity of this large class of materials, we should be cautious about claiming the same physics is dominant in all the materials.

There is a nice paper that illustrates the richness of this system.
Local Quantum Criticality of an Iron-Pnictide Tetrahedron 
T. Tzen Ong and Piers Coleman

It shows how the Hund's rule coupling and interplay of orbital and spin degrees of freedom can suppress formation of the Fermi liquid state that would occur in a one band system.

One of our key observations, is that in addition to their spin physics, the iron-based tetrahedra develop an orbital degree of freedom associated with the degenerate eg orbitals. For conventional transition metal ions, the Hund’s coupling JH locks the unpaired electrons together into a high-spin configuration, exponentially suppressing the spin-Kondo temperature to low temperatures according to an effect discovered by Schrieffer [15] and recently noted by others [16]. Here we show that unlike their spin counterparts, orbital fluctuations are not subject to the “Schrieffer effect”, giving rise to a unique situation in which the orbital degrees of freedom behave as fluctuating quantum mechanical variables that result in an incoherent “non-Fermi liquid” ground state. While departures from perfect tetragonality will reestablish the Fermi liquid, a large temperature range of incoherent metal behavior is expected to remain.

One of the effects of the projection into the high-spin manifold is an S-fold reduction of the spin-Kondo coupling, JS=J/4S but strikingly, the strength of the orbital Kondo interaction is unaffected. This means that the Hund’s interaction will exponentially suppress the spin-Kondo effect down to a lower scale TspinK/D∼(TorbK/D)2S, as in conventional transition metal ions, while leaving the orbital Kondo effect unaffected. This schism between the orbital and spin-Kondo effect drastically affects the physics,

Some positive changes for Australian undergraduates

Recently I was asked about how universities around the world are changing. I found my answer a bit depressing, as I see most of the changes as negative. However, the other day I reflected on some positive changes that have occurred at Australian universities since I was an undergraduate at the Australian National University (ANU), 35 years ago.
[There are also some significant negative changes, but I just want to acknowledge some positives].
I think some of these positives are particularly well done by my department, and by UQ, but I think they are also present at other universities.

Outreach to high school students.
A host of different programs bring students on campus for a range of activities. Faculty or "outreach officers" visit high schools. Although, ANU did run a friday afternoon math club for high school nerds in Canberra [where I grew up], I never had the opportunity to participate in a program such as the Queensland Junior Physics Olympiad.

International exchange programs.
No such program existed when I was an undergrad at ANU. I believe such a program only began at ANU about ten years later, when David Sholl was the first to make use of it. Now at UQ, students can study overseas for one or two semesters, at a diverse set of universities, some of which are better than UQ.

Summer research scholarships.
These programs were just beginning when I was an undergrad, and I never got to do one. In contrast, many UQ undergrads have done several such projects by the time they graduate.

Removal of terrible teachers.
At ANU I was privileged to have some outstanding and inspiring teachers including Hans Buchdahl, Hans Hornung, Neil Trudinger, and John Hutchinson. However, there were several lecturers who were absolutely shocking. They were "research inactive", waiting for retirement, and completely incomprehensible. There was no point in going to their lectures or taking any course they were responsible for. This is why I never did Solid State Physics or advanced Physical Chemistry as an undergraduate. I could be wrong, but I think that at most Australian universities such people have now been removed [or died] or are simply kept away from undergrads. They are too much of a liability, given concerns about keeping students happy. Mind you, I have to acknowledge by own department did allow such an individual to teach most of an undergrad course until ten years ago.

I found it refreshing to reflect on these positives.

Are holographic metals real or an illusion?

In 2010 MIT put out a press release about connections between string theory and cuprate superconductors that led to some breath taking articles in the media discussed on Peter Woit's blog.

The key issue is whether holographic techniques produce results that are relevant to real materials.

It is interesting to look at a recent paper
Holographic duality and the resistivity of strange metals
Richard A. Davison, Koenraad Schalm, and Jan Zaanen

They state

Analyses of this kind [based on the AdS-CFT correspondence] have found examples of systems, controlled by quantum critical infrared fixed points, with linear resistivities, among other interesting phenomena. While interesting, many of these results appear to be highly dependent upon the microscopic details of the infrared fixed point being considered, and, a priori, it is not clear whether these details are generic and could be realized in real electron systems, or whether they are artefacts of the kinds of highly symmetric quantum field theories that are dual to classical theories of gravity.

They then give a heuristic ["hand waving"] argument to "arrive at the stunning conclusion"

The resistivity is proportional to the entropy S(T). If the latter has the Sommerfeld form [characteristic of a Fermi liquid] then the resistivity is linear in temperature.

Here, l is the "characteristic length scale" over which "translational invariance is broken" due to the presence of quenched disorder. In order to agree with experiment it is required that l ~ 10 Angstroms ~ a lattice constant [n.b. this requires samples to be very dirty].

In order to get similar results from holographic techniques from string theory the authors have to make two very specific and strong assumptions

1. local quantum criticality, i.e. the dynamical exponent z is infinity
2. quenched disorder

Concerning the essential role played by the dependence on disorder the authors state:

This sheds new light on the long-standing puzzle of why the strong chemical disorder that is known to be intrinsic to cuprate crystals is not imprinted on their residual resistivity. It may also explain why the effects of electron-phonon couplings appear to be invisible in the electronic transport properties.

I don't follow the arguments here.
It seems to me that varying the disorder should change l and so change the resistivity and also lead to violations of Matthiessen's rule. Indeed, this paper does report a change in the slope of the resistivity versus temperature with the change in the concentration of zinc impurities.

The authors conclude

Our mechanism cannot explain either the high value of Tc or the T dependence of the Hall angle [61,62] in the cuprates. In particular, an explanation of the Hall angle may require the presence of an independent relaxation time associated with Hall transport, unlike in the hydrodynamic model we have outlined, in which all transport is controlled by the momentum relaxation time.

This shortcoming was one highlighted by Phil Anderson in his critical letter to Physics Today. Any credible theory of the unusual metallic state in the cuprates must explain a whole range of transport properties, not just the resistivity.

Furthermore, as highlighted in Ref. [63], linear resistivities with a “Planckian” momentum relaxation rate occur in a large variety of systems, including simple metals in the phonon-dominated regime, and heavy-fermion-like systems. Phonon domination is the most deadly adversary of the hydrodynamic liquid we have described, while the heavy fermion systems acquire their name from their large specific heats that tend to diverge upon decreasing the temperature toward their quantum critical points. Moreover, these systems are much cleaner than the cuprates, and we therefore do not see any reason to believe that our mechanism applies in these cases.

This contradicts claims in the MIT press release of relevance of holography to heavy fermions. It also contradicts claims of Sean Hartnoll that AdS-CFT and his conjectured diffusion bound is relevant to Ref. 63, work that I critiqued here.

Experimental workshop on grant applications

It is currently grant writing season in Australia. Arghh...!

Writing grant applications is a painful and demanding process. It is bad enough for old timers like me, but even worse for beginners. In the School of Mathematics and Physics at UQ, we are experimenting with different ways to support applicants and provide constructive feedback. Previously, I spoke at one such workshop.

We already have a "Reader" program where applicants give their whole application (50-100 pages) to a senior faculty member for feedback. However, I don't think this program gets used as much as it might or should be. That includes by me!
By the time I have finished the application I am sometimes so "burnt out" I don't want to spend time and energy changing it.
This highlights the importance of early feedback: even before the writing starts, when people are picking projects, co-investigators, and planning budgets.

Today we tried something different. About twenty people came to a meeting (with a free afternoon tea!), with a good mix of senior and junior people.

The following then happened.

A volunteer had 3 minutes to do the following:

Write the title of their grant application on the whiteboard.
Give the names of the Chief Investigators and Partner Investigators (outside Australia).
Write the total requested budget.
State why the project was important.
Explain why they were the best person to do the research.

The audience then asked questions and gave feedback. I think this was a little daunting for the volunteers, but they still did it.
People seemed to think this was a worthwhile exercise.
I thought it was pretty illuminating. It highlighted that you really need to have a sharp and clear message, and a realistic budget.

I welcome suggestions of other ideas on how other departments improve the quality of applications.

Quantum limits to the shear viscosity in the unitary Fermi gas

Previously, I posted about possible quantum limits to the shear viscosity in quantum many-body systems. This has attracted a lot of interest because of claims, based on string theory techniques [AdS-CFT correspondence] that there is a universal lower bound for the ratio of the shear viscosity to the entropy.

There are two interesting papers

Hydrodynamic fluctuations and the minimum shear viscosity of the dilute Fermi gas at unitarity
Clifford Chafin and Thomas Schäfer

Temperature evolution of the shear viscosity in a unitary Fermi gas 
 Gabriel Wlazłowski, Piotr Magierski, Aurel Bulgac, and Kenneth J. Roche

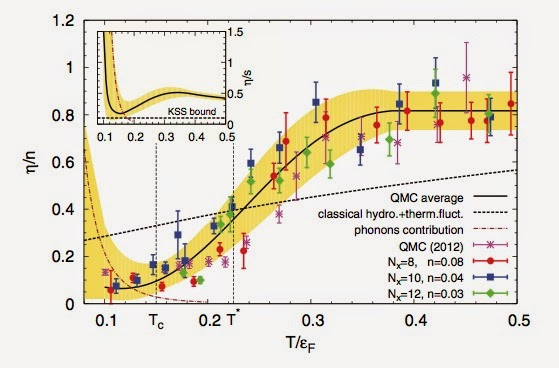
The main result of the latter is shown in the Figure below. The error bars arise because the results are based on a Quantum Monte Carlo simulation with imaginary time data that must be analytically continued to real frequencies [a thorny problem]. Tc is the superfluid transition temperature and T* the pseudogap temperature.

A few reasons why this is interesting.

1. In 1936 the legendary theoretical chemist Henry Eyring proposed a lower bound for the viscosity of n hbar, where n is the particle density. Here, we see that bound is violated.

2. The inset shows that the string theory bound is respected.

3. At low temperatures, the "classical" bound of about 0.2 n hbar, proposed in the first paper is violated.

4. The temperature dependence shows this is a strongly correlated fermion fluid, a long way from a Fermi liquid. For the latter, such as liquid 3He, the viscosity at low temperatures goes like 1/T^2, i.e. increases as the temperature decreases, and is much larger than n hbar. The fermion fluid here is something like a "bad metal" since these small viscosities correspond to mean free paths comparable to the Fermi wavelength.