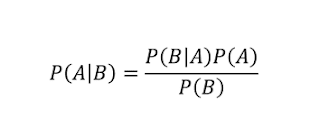Emergence and the Ising model

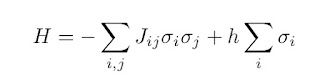
The Ising model is emblematic of “toy models” that have been proposed and studied to understand and describe emergent phenomena. Although originally proposed to describe ferromagnetic phase transitions, variants of it have found application in other areas of physics, and in biology, economics, sociology, neuroscience, complexity theory, …  

Quanta magazine had a nice article marking the model's centenary.

In the general model there is a set of lattice points {i} with a “spin” {sigma_i = +/-1} and a Hamiltonian

where h is the strength of an external magnetic field and J_ij is the strength of the interaction between the spins on sites i and j. The simplest models are where the lattice is regular, and the interaction is uniform and only non-zero for nearest-neighbour sites.

The Ising model illustrates many key features of emergent phenomena. Given the relative simplicity of the model, exhaustive studies since its proposal in 1920, have given definitive answers to questions often debated about more complex systems. Below I enumerate some of these insights: novelty, quantitative change leads to qualitative change, spontaneous order, singularities, short-range interactions can produce long-range order, universality, three horizons/scales of interest, self-similarity, inseparable horizons, and simple models can describe complex behaviour.

Most of these properties can be illustrated with the case of the Ising model on a square lattice with only nearest-neighbour interactions (J_ij = J). Above the critical temperature (Tc = 2.25J), and in the absence of an external magnetic field the system has no net magnetisation. Below Tc, at net magnetisation occurs. For J > 0 (J < 0) this state is ferromagnetic (antiferromagnetic).

Novelty

The state of the system below Tc is qualitatively different than that at very high temperatures or the state of a set of non-interacting spins. Thus, the non-zero magnetisation is an emergent property, as defined in this post. This state is also associated with spontaneous symmetry breaking and more than one possible equilibrium state, i.e., the magnetisation can be positive or negative.

Quantitative change leads to qualitative change

The qualitative change associated with formation of the magnetic state can occur with a small quantitative change in the value of the ratio T/J, i.e., either by decreasing T or increasing J. Formation of the magnetic state is also associated with the quantitative change of increasing the number of spins from a large finite number to infinity. 

Singularities

For a finite number of spins all the thermodynamic properties of the system are an analytic function of the temperature and magnitude of an external field. However, in the thermodynamic limit, these properties become singular at T=Tc and h=0. This is the critical point in the phase diagram of h versus T. Some of the quantities, such as the specific heat capacity and the magnetic susceptibility, become infinite at the critical point. These singularities are characterised by critical exponents, most of which have non-integer values. Consequently, the free energy of the system is not an analytic function of T and h.

Spontaneous order

The magnetic state occurs spontaneously. The system self-organises. There is no external field causing the magnetic state to form. There is long-range order, i.e., the value of spins that are infinitely apart from one another are correlated. 

Short-range interactions can produce long-range order.

Although there is no direct long-range interaction between spins, long-range order can occur. Prior to Onsager’s exact solution of the two-dimensional model, many scientists were not convinced that this was possible.

Universality

The values of the critical exponents are independent of many details of the model, such as the value of J, the lattice constant and spatial anisotropy, and the presence of small interactions beyond nearest neighbour. Many details do not matter. This is why the model can give a quantitative description of experimental data near the critical temperature, even though the model Hamiltonian is a crude descriptions of the interactions in a real material. It can describe not only magnetic transitions but also transitions in liquid-gas, binary alloys, and binary liquid mixtures.

Three horizons/scales of interest

There are three important length scales associated with the model. Two are simple: the lattice constant, and the size of the whole lattice. These are the microscopic and macroscopic scale. The third scale is emergent and temperature dependent: the correlation length, i.e., the distance over which spins are correlated with one another. This can also be visualised as the size of magnetisation domains seen in Monte Carlo simulations. 

The left, centre, and right panels above show a snapshot of a likely configuration of the system at a temperature less than, equal to, and greater than the critical temperature, Tc, respectively.

Understanding the connection between the microscopic and macroscopic properties of the system requires studying the system at the intermediate scale of the correlation length. This scale also defines emergent entities [magnetic domains] that interact with one another weakly and via an effective interaction.

Self-similarity

At the critical temperature, the correlation length is infinite. Consequently, rescaling the size of the system, as in a renormalisation group transformation, the state of the systems does not change. The system is said to be scale-free or self-similar like a fractal pattern. This is an example of self-organised criticality.

Inseparable horizons

I now consider how things change when the topology or dimensionality of the lattice changes or when interactions beyond nearest neighbours are added. This can change the relationships between the parts and the whole. Some details of the parts matter. Changing from a two-dimensional rectangular lattice to a linear chain the ordered state disappears. Changing to a triangular lattice with antiferromagnetic nearest-neighbour interactions removes the ordering at finite temperature and there are an infinite number of ground states at zero temperature. Thus, some microscopic details do matter.

The main point of this example is that to understand a large complex system we have to keep both the parts and the whole in mind. It is not either/or but both/and. Furthermore, there may be an intermediate scale, at which new entities emerge.

Aside: I suspect heated debates about structuralism versus functionalism in social sciences, and the humanities are trying to defend intellectual positions (and fashions) that overlook the inseparable interplay of the microscopic and macroscopic that the Ising model captures.

Simple models can describe complex behaviour

Now consider an Ising model with competing interactions, i.e. the neighbouring spins of a particular spin compete with one another and with an external magnetic field to determine the sign of the spin. This can be illustrated with the an Ising model on a hexagonal close packed (hcp) lattice with nearest neighbour antiferromagnetic interactions and an external magnetic field. The lattice is frustrated and can be viewed as layers of hexagonal (triangular) lattices where each layer is displaced relative to one another.

This model has been studied by materials scientists as it can describe the many possible phases of binary alloys, AxB1-x, where A and B are different chemical elements (for example, silver and gold) and the Ising spins on site i has value +1 or -1, corresponding to the presence of atom A or B on that site. The magnetic field corresponds to the difference in the chemical potentials of A and B, and is related to their relative concentration.

The authors studied the Ising model on the hexagonal close-packed (hcp) lattice in a magnetic field. The authors are all from materials science departments and are motivated by the fact that the problem of binary alloys AxB1_x can be mapped onto an Ising model. A study of this model found rich phase diagrams including 32 stable ground states with stoichiometries, including A, AB, A2B, A3B, A5B, and A4B3. Even for a single stoichiometry, there can be multiple possible distinct orderings (and crystal structures). Of these structures, six are stabilized by purely nearest-neighbour interactions, eight by addition of next-nearest neighbour interactions. The remaining 18 structures require multiplet interactions for their stability. 

A second example is the Anisotropic Next-Nearest Neighbour Ising (ANNNI) model, which supports a plethora of ordered states, including a phase diagram with a fractal structure, known as the Devil’s staircase.

These two Ising models illustrate how relatively simple models, containing competing interactions (described by just a few parameters) can describe rich behaviour, particularly a diversity of ground states.

David Mermin on his life in science: funny, insightful, and significant

 David Mermin has posted a preprint with the modest title, Autobiographical Notes of a Physicist

There are many things I enjoyed and found interesting about his memories. A few of the stories I knew, but most I did not. He reminisces about his interactions with Ken Wilson, John Wilkins, Michael Fisher, Walter Kohn, and of course, Neil Ashcroft.

Mermin is a gifted writer and can be amusing and mischievous. He is quite modest and self-deprecating about his own achievements.

He explains why we should refer to the Hohenberg-Mermin-Wagner theorem, not Mermin-Wagner.

One of his Reference Frame columns in Physics Today, stimulated Paul Ginsbarg to start the arXiv.

I was struck by how Mermin's career belongs to a different era. The community was smaller and more personal. Doing physics was fun. Time was spent savouring the pleasure of learning new things and explaining them to others. Colleagues were friends rather than competitors. His research was curiosity-driven. This led to Mermin making significant contributions to quantum foundations. And, he only published about two papers per year!

Teaching was valued, enjoyable, and stimulated research. It was also a way to learn a subject, regardless of the level at which it was taught. For eight years, Mermin and Ashcroft spent half their time writing their beautiful textbook!

I look forward to hearing others' reflections.

Wading through AI hype about materials discovery

 Discovering new materials with functional properties is hard, very hard. We need all the tools we can from serendipity to high-performance computing to chemical intuition. 

At the end of last year, two back-to-back papers appeared in the luxury journal Nature.

Scaling deep learning for materials discovery

All the authors are at Google. They claim that they have discovered more than two million new materials with stable crystal structures using DFT-based methods and AI.

On Doug Natelson's blog there are several insightful comments on the paper about why to be skeptical about AI/DFT based "discovery".

Here are a few of the reasons my immediate response to this paper is one of skepticism.

It is published in Nature. Almost every "ground-breaking" paper I force myself to read is disappointing when you read the fine print.

It concerns a very "hot" topic that is full of hype in both the science and business communities.

It is a long way from discovering a stable crystal to finding that it has interesting and useful properties.

Calculating the correct relative stability of different crystal structures of complex materials can be incredibly difficult.

DFT-based methods fail spectacularly for the low-energy properties of quantum materials, such as cuprate superconductors. But, they do get the atomic structure and stability correct, which is the focus of this paper.

It is a big gap between discovering a material that has desirable technological properties to one that meets the demanding criteria for commercialisation.

The second paper combines AI-based predictions, similar to the paper above, with robots doing material synthesis and characterisation.

An autonomous laboratory for the accelerated synthesis of novel materials

[we] realized 41 novel compounds from a set of 58 targets including a variety of oxides and phosphates that were identified using large-scale ab initio phase-stability data from the Materials Project and Google DeepMind

These claims have already been undermined by a preprint from the chemistry departments at Princeton and UCL.

Challenges in high-throughput inorganic material prediction and autonomous synthesis

We discuss all 43 synthetic products and point out four common shortfalls in the analysis. These errors unfortunately lead to the conclusion that no new materials have been discovered in that work. We conclude that there are two important points of improvement that require future work from the community: 

(i) automated Rietveld analysis of powder x-ray diffraction data is not yet reliable. Future improvement of such, and the development of a reliable artificial intelligence-based tool for Rietveld fitting, would be very helpful, not only to autonomous materials discovery, but also the community in general.

(ii) We find that disorder in materials is often neglected in predictions. The predicted compounds investigated herein have all their elemental components located on distinct crystallographic positions, but in reality, elements can share crystallographic sites, resulting in higher symmetry space groups and - very often - known alloys or solid solutions. 

Life is messy. Chemistry is messy. DFT-based calculations are messy. AI is messy. 

Given most discoveries of interesting materials often involve serendipity or a lot of trial and error, it is worth trying to do what the authors of these papers are doing. However, the field will only advance in a meaningful way when it is not distracted and diluted by hype and authors, editors, and referees demand transparency about the limitations of their work.  

Certain benefits of Bayes

Best wishes for the New Year! One thing I hope to achieve this year is an actual understanding of things "Bayesian".

I am particularly interested because it gives a way to be more quantitative and precise about some of the intuitions that I use in science. For example, I tend to be skeptical of new experimental results (often hyped) that claim to go against well-established theories, regardless of how good the "statistics" of the touted result.

In this vein, Phil Anderson argued that Bayesian methods should have been used to rule out the significance of "discoveries" such as the 10 keV neutrino and the fifth force. In 1992 he wrote a Physics Today column on the subject.

An interesting metric for mathematical formula is the ratio of profound and wide implications to the simplicity of the formula and its derivation. I suspect that Bayes' formula for conditional probabilities would win first place!

P(A|B) denotes the probability of A given B. 

The proof takes about two lines. If you multiply both sides of the equation about by P(B) the identity holds because both sides of the equation are just different ways of writing P(A and B).

My first attempt to understand the applications and implications of Bayes was reading the relevant sections in Phil Nelson's beautiful book, Physical Models of Living Systems. There is a helpful section entitled, "Bayes formula provides a consistent approach to upgrading our degree of belief in light of new data."

More recently, I found this wonderful and short video very helpful, as it clearly defines terms, uses graphical representations, and gives some concrete examples.

 

A Bayesian perspective highlights the importance of reporting negative results and is the basis of a seminal paper

Why Most Published Research Findings Are False by John P. A. Ioannidis

A measure of the profundity of Bayes is that the Stanford Encyclopedia of Philosophy has two articles on the topic

Bayes Theorem

Bayesian Epistemology