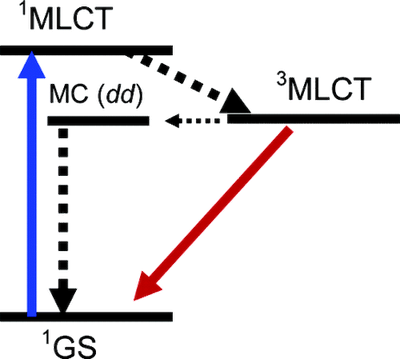
 One then uses the following two equations to deduce the radiative and non-radiative decay rates.
One then uses the following two equations to deduce the radiative and non-radiative decay rates.For just one of many examples, of how this is done, see this paper, by Lawrence Lo and collaborators.
 One then uses the following two equations to deduce the radiative and non-radiative decay rates.
One then uses the following two equations to deduce the radiative and non-radiative decay rates.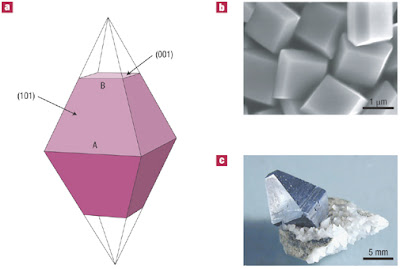 Today Max Lu is giving the weekly Physics Colloquium. No doubt, one thing he will talk about is how his group was able to grow large single crystals of the anatase form of TiO2 (titanium dioxide) with a large percentage of reactive facets. (It is described in this Nature paper). A key component of that work was that DFT calculations helped guide the chemical synthesis strategy.
Today Max Lu is giving the weekly Physics Colloquium. No doubt, one thing he will talk about is how his group was able to grow large single crystals of the anatase form of TiO2 (titanium dioxide) with a large percentage of reactive facets. (It is described in this Nature paper). A key component of that work was that DFT calculations helped guide the chemical synthesis strategy.


 This weeks reading from Phillips, Advanced Solid State Physics, is Section 8.4, on the dielectric response function. This is calculated at the level of the Random-Phase-Approximation (RPA) for a Fermi liquid (weakly interacting fermion gas). One finds the density-density response function. The imaginary part is related to the structure factor (via a fluctuation-dissipation relation). This can be thought of as an effective density of states for particle-hole excitations.
This weeks reading from Phillips, Advanced Solid State Physics, is Section 8.4, on the dielectric response function. This is calculated at the level of the Random-Phase-Approximation (RPA) for a Fermi liquid (weakly interacting fermion gas). One finds the density-density response function. The imaginary part is related to the structure factor (via a fluctuation-dissipation relation). This can be thought of as an effective density of states for particle-hole excitations.  In today's lecture I discussed ideal solutions and osmotic pressure. This illustrates the surprising fact that the thermodynamics of dilute solutions is dominated by entropic effects and much of the conceptual formalism of mixing of ideal gases can be carried over, even though the interaction of the solute with the solvent molecules may be highly non-trivial.
In today's lecture I discussed ideal solutions and osmotic pressure. This illustrates the surprising fact that the thermodynamics of dilute solutions is dominated by entropic effects and much of the conceptual formalism of mixing of ideal gases can be carried over, even though the interaction of the solute with the solvent molecules may be highly non-trivial.


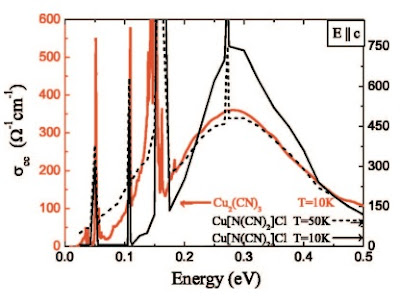




 A few random observations:
A few random observations:

 Tomorrow I am giving my first lecture using clickers!
Tomorrow I am giving my first lecture using clickers!
Novelty. Temperature and entropy are emergent properties. Classically, they are defined by the zeroth and second laws of thermodynamics, re...