the increasing modularisation of university curricula has meant that the connections between different areas of mathematics are not always made apparent. Indeed, for many students who attended schools in England, their pre-university experience of mathematics is that it is presented as a range of topics to be mastered for assessment, and which can then be completely forgotten as the learner moves on to the next module. Undergraduates today often express surprise when they discover that a topic covered earlier in the curriculum is required elsewhere later. This attitude is profoundly depressing: do students really think that we are encouraging them to put enormous effort into learning things that are going to be of no future value?The review also recommends several other texts for Capstone courses. I would be interesting in any recommendations for physics courses.
Saturday, December 31, 2011
Capping it all off
The Times Higher Education Supplement has a nice book review of a new text So thats how it all fits together by the celebrated mathematician John B. Conway. The book is designed for a "capstone" course at the end of a mathematics undergraduate degree. I thought the following introductory paragraph was helpful, and just as relevant to physics undergraduate education (at least in Australia):
Thursday, December 29, 2011
iPoverty
The New York Times has a nice article by Thomas Friedman, The Last Person about the Indian Institute for Technology in Rajasthan developing an extremely cheap tablet computer that is affordable [with some government subsidy] to the extremely poor.
Teaching scientific research methods
How does someone learn to do good research? Most scientists might claim it is by osmosis and experience. Social scientists tend to make graduate students take formal courses in "research methods". In contrast, natural scientists seem quite skeptical to such approaches.
Michael Marder has a new book out Research Methods for Science. It looks quite worthwhile because of the mix of background, hands on exercises, practical advice, statistics, .... It is based on a course he has co-taught to undergraduate science majors for a number of years at UTexas.
I welcome comments, particularly from people who have taught or taken such courses.
Michael Marder has a new book out Research Methods for Science. It looks quite worthwhile because of the mix of background, hands on exercises, practical advice, statistics, .... It is based on a course he has co-taught to undergraduate science majors for a number of years at UTexas.
I welcome comments, particularly from people who have taught or taken such courses.
Wednesday, December 28, 2011
Careers should be driven by scientific reality not metrics
More and Different by Phil Anderson is stimulating and challenging holiday reading. Here is a paragraph from an essay, "Reflections on Twentieth Century Physics," which considers how from the 1950s to the end of the century:
I consider this is a painfully accurate description of the current reality. It is amazing to see how few papers [one or two per year] the leaders published back in the 50s and 60s.
Is there anyway out of this undesirable situation? We can't turn back the clock. However, we can all [both junior and senior scientists] exercise some critical judgement and self control and not be completely conformed to the system and our colleagues.
Keep the science at the forefront of our minds and pre-occupations, don't jump on the latest band-wagon or become obsessed with the latest "metric" of productivity.
Photo is Anderson and Richards looking at apparatus for experiments on superfluid 4He at Bell labs (in the 1960s) taken from the AIP archives.
There was a very sharp change in the nature of a research career. The "promising" young scientists publication rate grew by factors of five to ten; the number of applications a young researcher might make for post-doctoral work or an entry-level position rose from two or three to 50. Senior scientists were overwhelmed with receiving and sending reams of letters of recommendation, which thereupon became meaningless. The numbers of meetings .. grew by factors of ten or more... Most publications became tactical in this game of jockeying one's way to the top; publications in certain prestige journals were seen as essential entry tickets or score counters rather than as serious means of communication. Great numbers of these publications were about simulations of dubious realism or relevance. Essentially, in the early part of the post-war period the career was science-driven, motivated mostly by absorption with the great enterprise of discovery, and by genuine curiosity as to how nature operates. But the last decade of the century far too many, especially of the young people, were seeing science as a competitive interpersonal game, in which the winner was not the one who was objectively right as the the nature of scientific reality but the one who was successful at getting grants, publishing in PRL, and being noticed in the news pages of Nature, Science, or Physics Today.More and Different, page 100.
I consider this is a painfully accurate description of the current reality. It is amazing to see how few papers [one or two per year] the leaders published back in the 50s and 60s.
Is there anyway out of this undesirable situation? We can't turn back the clock. However, we can all [both junior and senior scientists] exercise some critical judgement and self control and not be completely conformed to the system and our colleagues.
Keep the science at the forefront of our minds and pre-occupations, don't jump on the latest band-wagon or become obsessed with the latest "metric" of productivity.
Photo is Anderson and Richards looking at apparatus for experiments on superfluid 4He at Bell labs (in the 1960s) taken from the AIP archives.
Friday, December 23, 2011
What is a metal?
How does one distinguish a metal from an insulator? One signature might be the presence of a charge gap at the chemical potential.
Is there a broken symmetry associated with a metal-insulator phase transition?
A key concept emphasized by Anderson is that distinct phases of matter are associated with the rigidity of their order parameter. For example, for a superconductor the superfluid density is associated with the phase stiffness of the ground state wave function.
It turns out that the Drude weight and the charge compressibility are both zero in a Mott insulator and non-zero in a metal. This is discussed in an interesting article by Imada.
Aside: Imada's paper assumes the metal-insulator transition is continuous (i.e. not first-order) and derives scaling relations for the transition. This assumption may not be valid. At least, in dynamical mean-field theory the Mott transition at half filling is first order.
Kohn (and later Thouless) emphasized that for a metal one could calculate the Drude weight from the size and twist dependence of the ground state energy in the presence of twisted boundary conditions.
Imada considered a system at finite temperature and considered twisted boundary conditions in the imaginary time direction [anti-periodicity for fermions is required by the Kubo-Martin-Schwinger condition] showed that the charge compressibility determines the twist dependence.
I would be interested to see how the Drude weight and charge compressibility vary as one increases the temperature through the Fermi liquid - bad metal crossover.
Is there a broken symmetry associated with a metal-insulator phase transition?
A key concept emphasized by Anderson is that distinct phases of matter are associated with the rigidity of their order parameter. For example, for a superconductor the superfluid density is associated with the phase stiffness of the ground state wave function.
It turns out that the Drude weight and the charge compressibility are both zero in a Mott insulator and non-zero in a metal. This is discussed in an interesting article by Imada.
Aside: Imada's paper assumes the metal-insulator transition is continuous (i.e. not first-order) and derives scaling relations for the transition. This assumption may not be valid. At least, in dynamical mean-field theory the Mott transition at half filling is first order.
Kohn (and later Thouless) emphasized that for a metal one could calculate the Drude weight from the size and twist dependence of the ground state energy in the presence of twisted boundary conditions.
Imada considered a system at finite temperature and considered twisted boundary conditions in the imaginary time direction [anti-periodicity for fermions is required by the Kubo-Martin-Schwinger condition] showed that the charge compressibility determines the twist dependence.
I would be interested to see how the Drude weight and charge compressibility vary as one increases the temperature through the Fermi liquid - bad metal crossover.
Thursday, December 22, 2011
Dialectic model building
Phil Anderson makes the following interesting comment [in the context of Cooper's treatment of the "pairing" problem] about model building in research.
I would argue that this approach has largely been abandoned in theoretical chemistry due to the dominance of computational chemistry.
Actually, in almost every case where I have been really successful it has been by dint of discarding almost all of the apparently relevant features of reality in order to create a “model” which has the two almost incompatible features:
(1) enough simplicity to be solvable, or at least understandable;
(2) enough complexity left to be interesting, in the sense that the remaining complexity actually contains some essential features which mimic the actual behavior of the real world, preferably in one of its as yet unexplained aspects.
I said dangerous, and the sense in which this is true is that one is laying a trap for the majority of one’s colleagues, who are too literal-minded to understand either the necessity or the reality of the model-building process. A really well-built model can often stand a great deal of weight if used judiciously, but it can never hold up against being taken completely literally.P.W. Anderson, "BCS" and Me, More and Different, page 38.
I would argue that this approach has largely been abandoned in theoretical chemistry due to the dominance of computational chemistry.
Wednesday, December 21, 2011
A signature of a "two fluid" picture for a strongly correlated electron system
This post connects two seemingly disparate research topics of interest to me: optical properties of organic molecules and low energy excitations of strongly correlated electron materials. The connecting concept is that of an isosbestic point.
The figure below shows the absorption spectrum of an organic dye for a range of pH values. Note that there is a wavelength (around 500 nm) at which all the spectra appear to cross. This is called the isosbestic point. Varying the pH varies the relative concentration of two forms of the dye molecule. Each form has a characteristic absorption peak (centred at lambda_1 and lambda_2 in the figure). The isosbestic point occurs at the wavelength at which the absorption due to each of the molecular forms has the same intensity. Hence, at this wavelength varying the relative concentration does not change the absorption intensity.
So what does this have to do with strongly correlated electron materials?In 1997 Dieter Vollhardt published a PRL, Characteristic Crossing Points in Specific Heat Curves of Correlated Systems which pointed out that in liquid 3He, some heavy fermion materials, and the Hubbard model (solved by dynamical mean-field theory (DMFT)) there was a temperature at which the specific heat curves for different pressures (or Hubbard U or magnetic field) all crossed. Below is shown the data for liquid 3He. The crossing temperature is approximately that at which Fermi liquid theory breaks down.
Below are the curves for the Hubbard model.
This is not an artefact of DMFT since later Chandra, Kollar, and Vollhardt showed it is also present for the exact solution of the one-dimensional model.
I find this quite amazing!
Vollhardt made no mention of isosbestic points which I think would have been well known to many chemists. But, in 2007 there is Isosbestic Points in the Spectral Function of Correlated Electrons by Martin Eckstein, Marcus Kollar and Dieter Vollhardt.
It contains a nice discussion of the essential physics, including the connection to the spectra of dye molecules.
The paper contains the figure below of the spectral density for a Hubbard model (calculated with DMFT). The horizontal scale is frequency (omega) and the dashed curve is the non-interacting density of states.
So what does this all mean?
The key idea is one of "two fluids" i.e., that as one varies the relevant parameter (pressure, magnetic field or Hubbard U) all one is doing is varying the relative concentration of the two fluids. A sum rule requires one fluid must be converted into another. In the case of the Hubbard model the total number of electrons (area under A(omega)) is conserved. As one increases U one decreases the spectral weight in the Fermi liquid component (centred at omega=0) and increases the weight of the Hubbard bands (centred at omega=+-U/2).
Tuesday, December 20, 2011
One view from the trenches
The Heckler is a column in the Sydney Morning Herald where "Readers are invited to send 450 words about what makes their blood boil."
This week Nick Coleman had a piece "You could do this or go fishing" about the process for applying for research grants in Australia.
This week Nick Coleman had a piece "You could do this or go fishing" about the process for applying for research grants in Australia.
Observing the geometric phase in magnetoresistance II
Previously I posted how one could see a signature of Berry's geometric phase in Shubnikov de Haas experiments on graphene. Similar experiments and analysis of data for topological insulators produces ambiguous results, as discussed in this recent PRB by Taskin and Ando. In particular, the Berry phase gamma can be extracted from a "Landau level fan diagram" where one plots the inverse of the magnetic field B vs. the Landau level index N. Taskin and Ando claim that in the topological insulator the dispersion relation E(k) is non-linear and as a result
1. the fan diagram is non-linear
2. the Berry phase gamma deviates from pi and is a function of B
I am confused by 2. I would have thought that topology would require gamma to be only be pi or 0. This could be checked by looking at the eigenfunctions for the non-linear dispersion. Am I missing something?
The above claims are based on eqn. 8 in the paper. It is derived from the generalised Onsager condition which is a semi-classical condition relating the area of the quantised cyclotron orbit to Landau level index N.
I welcome clarifications.
1. the fan diagram is non-linear
2. the Berry phase gamma deviates from pi and is a function of B
I am confused by 2. I would have thought that topology would require gamma to be only be pi or 0. This could be checked by looking at the eigenfunctions for the non-linear dispersion. Am I missing something?
The above claims are based on eqn. 8 in the paper. It is derived from the generalised Onsager condition which is a semi-classical condition relating the area of the quantised cyclotron orbit to Landau level index N.
I welcome clarifications.
Saturday, December 17, 2011
More and Different
I have just started reading Phil Anderson's new book, More and Different: notes from a thoughtful curmudgeon. It is a collection of essays on wide ranging subjects: personal reminiscences, history, philosophy, sociology, science wars, ....
Some of these have been published before but many have not.
The history is fascinating and the science stimulating. I highly recommend the book and will hopefully post some highlights.
Last night I read the personal reminiscence "BCS and me" which gave me an even greater appreciation of just how tortuous the road to the theory was, how brilliant the solution was, and how it still left some important questions to be answered.
Some of these have been published before but many have not.
The history is fascinating and the science stimulating. I highly recommend the book and will hopefully post some highlights.
Last night I read the personal reminiscence "BCS and me" which gave me an even greater appreciation of just how tortuous the road to the theory was, how brilliant the solution was, and how it still left some important questions to be answered.
Friday, December 16, 2011
Strongly correlated electron systems in high magnetic fields II
When and how can a large magnetic field change the ground state of a strongly correlated electron metal?
An earlier post considered this question.
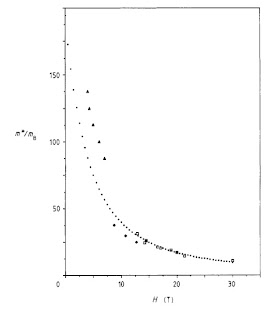
To me, one of the most striking cases is that of heavy fermion metals in high magnetic fields. From quantum magnetic oscillations [e.g., SdH and dHvA] one can measure the effective mass of the Fermi liquid quasi-particles. The figure below shows how in CeB6 the effective mass decreases significantly with increasing magnetic field. Hence, the field destroys the heavy fermion behaviour.
What is the physics behind this dramatic effect?The heavy fermion character arises from the formation of Kondo singlets between the localised spins and the conduction electrons. However, an external magnetic field breaks these singlets, reducing the heavy fermion character. The Kondo lattice temperature [coherence temperature] sets the relevant magnetic field scale and is well described by a slave boson theory of Wasserman, Springford, and Hewson [see eqn. 17 for m*(H)]. It also contains the above figure.
A more sophisticated treatment [connecting to recent NRG (Numerical Renormalisation Group) treatments of the single impurity Anderson model] of the case of YbRh2Si2 has recently been discussed by Zwicknagl. I am not clear on why she (and Hewson!) do not reference this earlier slave boson theory in their latest work.
The ultimate purpose of your teaching
There is an excellent New York Times online article What is College For? by Gary Gutting.
Here are just a few quotes to stimulate you to read the whole article.
Here are just a few quotes to stimulate you to read the whole article.
the university curriculum leaves students disengaged from the material they are supposed to be learning. They see most of their courses as intrinsically “boring,” of value only if they provide training relevant to future employment or if the teacher has a pleasing (amusing, exciting, “relevant”) way of presenting the material. As a result, students spend only as much time as they need to get what they see as acceptable grades (on average, about 12 to 14 hour a week for all courses combined). Professors have ceased to expect genuine engagement from students and often give good grades (B or better) to work that is at best minimally adequate. ....
the raison d’être of a college is to nourish a world of intellectual culture; that is, a world of ideas, dedicated to what we can know scientifically, understand humanistically, or express artistically.I thank my lovely wife for bringing the article to my attention.
Teachers need to see themselves as, first of all, intellectuals, Students, in turn, need to recognize that their college education is above all a matter of opening themselves up to new dimensions of knowledge and understanding.
It is more a matter of students moving beyond their interests than of teachers fitting their subjects to interests that students already have. Good teaching does not make a course’s subject more interesting; it gives the students more interests — and so makes them more interesting.
Thursday, December 15, 2011
Is Papers 2.1 an improvement?
I really love the program Papers for the Mac.
They just released version 2.1 and so I downloaded a trial version.
However, after a week I reverted back to my old version 1. I had trouble getting the "Match" and "Query" functions to work and so gave up.
I welcome alternative views and suggestions.
They just released version 2.1 and so I downloaded a trial version.
However, after a week I reverted back to my old version 1. I had trouble getting the "Match" and "Query" functions to work and so gave up.
I welcome alternative views and suggestions.
RG theory of turbulence
The renormalisation group and scaling has proven to be an extremely powerful technique in theoretical physics. It has even been succesfully applied to turbulence. A paper by Yakhot and Orczag in the Journal of Scientific Computing (!) is widely cited.
Wednesday, December 14, 2011
Observing the geometric phase in magnetoresistance I
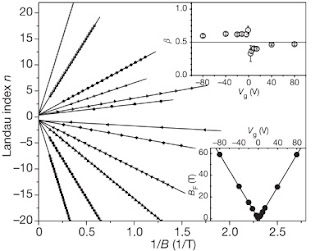
The geometric (or Berry's) phase in quantum mechanics does have experimental manifestations in macroscopic materials. For example it can be seen in the phase of Shubnikov de Haas oscillations. The graph below is based on experimental data for graphene, taken from a 2005 Nature paper. In this "fan diagram" the Landau level index is plotted versus 1/B [the magnetic field at which a peak in the resistance occurs]. The y-axis) intercept (shown in the upper right inset as a function of gate voltage) is related to the Berry phase, beta. For a linear Dirac spectrum, beta=1/2 and for a quadratic spectrum, beta=0.
Similar experiments and analysis of data for topological insulators produces ambiguous results, which I will discuss in a forthcoming post about this recent PRB.
Tuesday, December 13, 2011
The Nernst effect in strongly correlated electron materials
The Nernst effect is a thermal conduction analogue of the Hall effect for electrical conductivity, i.e., it measures the transverse electrical current induced by a longitudinal thermal current in the presence of a magnetic field perpendicular to both currents.
It was considered an obscure (and very small) effect in elemental metals. However, the past 15 years it has become a powerful probe of strongly correlated metals, initially because of its sensitivity to superconducting fluctuations, as discussed by Ong.
A nice helpful review is The Nernst Effect and the Boundaries of the Fermi Liquid Picture by Kamran Behnia.
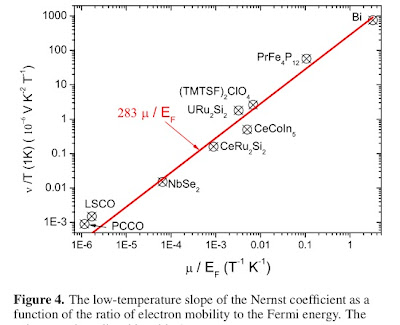
He argues that the magnitude of the Nernst signal at low temperatures for a wide range of materials is proportional to the ratio of the charge carrier mobility to the Fermi energy. This is supported by the Figure below. Note the logarithmic scales.
A few notes.
1. The simple Fermi liquid expression [equation (8)] gives the Nernst signal as proportional to the energy derivative of the scattering time. For a Fermi liquid form of the scattering rate, the energy dependence is quadratic, and the signal will vanish. Essentially Behnia's replacement of the the energy derivative by the ratio of the scattering time and the Fermi energy means he is assuming that the scattering has a marginal Fermi liquid form. This is worth considering in more detail.
2. As the temperature increases there should be a crossover from a Fermi liquid with coherent quasi-particles with well-defined wavevectors to a "bad metal" with incoherent excitations. How this is manifested in the Nernst signal is an outstanding question.
3. A PRB by Kontani has given a general expression for the Nernst coefficient in a Fermi liquid including vertex corrections. A detailed analysis (within the framework of FLEX) claims that vertex corrections are important and due to antiferromagnetic fluctuations a large Nernst signal is possible in the pseudogap phase. [See Section 5.2 of this review].
It was considered an obscure (and very small) effect in elemental metals. However, the past 15 years it has become a powerful probe of strongly correlated metals, initially because of its sensitivity to superconducting fluctuations, as discussed by Ong.
A nice helpful review is The Nernst Effect and the Boundaries of the Fermi Liquid Picture by Kamran Behnia.
He argues that the magnitude of the Nernst signal at low temperatures for a wide range of materials is proportional to the ratio of the charge carrier mobility to the Fermi energy. This is supported by the Figure below. Note the logarithmic scales.
A few notes.
1. The simple Fermi liquid expression [equation (8)] gives the Nernst signal as proportional to the energy derivative of the scattering time. For a Fermi liquid form of the scattering rate, the energy dependence is quadratic, and the signal will vanish. Essentially Behnia's replacement of the the energy derivative by the ratio of the scattering time and the Fermi energy means he is assuming that the scattering has a marginal Fermi liquid form. This is worth considering in more detail.
2. As the temperature increases there should be a crossover from a Fermi liquid with coherent quasi-particles with well-defined wavevectors to a "bad metal" with incoherent excitations. How this is manifested in the Nernst signal is an outstanding question.
3. A PRB by Kontani has given a general expression for the Nernst coefficient in a Fermi liquid including vertex corrections. A detailed analysis (within the framework of FLEX) claims that vertex corrections are important and due to antiferromagnetic fluctuations a large Nernst signal is possible in the pseudogap phase. [See Section 5.2 of this review].
Monday, December 12, 2011
What is the origin of magnetoresistance in silver chalcogenides?
Silver chalcogenides (e.g., Ag2Te) with slightly altered stoichiometry exhibit an unusual magnetoresistance. It is large and linear in field for magnetic fields up to about 6 tesla and temperatures between 5 and 300 K. [See this 1997 Nature paper].
Several possible physical origins of the magnetoresistance have been proposed.
1. A PRL earlier this year proposes is the material is a topological insulator with gapless surface states described by a highly anisotropic Dirac cone.
2. In 1998 Abrikosov proposed the materials are gapless semiconductors with a linear spectrum, doped to a small carrier concentration, and that only one Landau level contributes to the conductivity.
3. Parish and Littlewood's proposal that the key physics is that of a strongly spatially inhomogeneous semiconductor which can be described by a random resistor network.
4. I also note that a band structure which produces a non-zero Berry curvature can produce a linear magnetoresistance, according to p. 1984 of this Rev. Mod. Phys. [However, I suspect this is a very small effect].
The challenge is to come up with experimental signatures which can distinguish between the four different theoretical proposals.
Several possible physical origins of the magnetoresistance have been proposed.
1. A PRL earlier this year proposes is the material is a topological insulator with gapless surface states described by a highly anisotropic Dirac cone.
2. In 1998 Abrikosov proposed the materials are gapless semiconductors with a linear spectrum, doped to a small carrier concentration, and that only one Landau level contributes to the conductivity.
3. Parish and Littlewood's proposal that the key physics is that of a strongly spatially inhomogeneous semiconductor which can be described by a random resistor network.
4. I also note that a band structure which produces a non-zero Berry curvature can produce a linear magnetoresistance, according to p. 1984 of this Rev. Mod. Phys. [However, I suspect this is a very small effect].
The challenge is to come up with experimental signatures which can distinguish between the four different theoretical proposals.
Saturday, December 10, 2011
From every angle
I am enjoying re-reading the book 5 Minds for the Future by Howard Gardner. The 5 minds are Disciplined, Synthetic, Creative, Respectful, and Ethical.
With regard to all of the first three he puts emphasis on the importance of considering the same topic from several angles and perspectives. In particular, creative needs to occur within a context of mastering earlier work.
I wonder how might this does and might happen in condensed matter theory?
Phenomenological vs. microscopic.
Strong coupling vs. weak coupling treatments.
Numerical vs. variational wave functions vs. field theories vs. renormalisation group.
A "chemical" approach concerned with specific details vs. a "physics" approach which neglects many details.
Other ideas?
I actually wonder whether we actually do this more often and better than some disciplines. But that perception may be based on ignorance and hubris!
With regard to all of the first three he puts emphasis on the importance of considering the same topic from several angles and perspectives. In particular, creative needs to occur within a context of mastering earlier work.
I wonder how might this does and might happen in condensed matter theory?
Phenomenological vs. microscopic.
Strong coupling vs. weak coupling treatments.
Numerical vs. variational wave functions vs. field theories vs. renormalisation group.
A "chemical" approach concerned with specific details vs. a "physics" approach which neglects many details.
Other ideas?
I actually wonder whether we actually do this more often and better than some disciplines. But that perception may be based on ignorance and hubris!
Seeking a unified theory for unconventional superconductors II
Phil Anderson has written an interesting comment on my earlier post on this subject. His comment might be read in conjunction with two earlier posts that are revelant.
Glueing together a theory is relevant to his comment about whether the pairing interaction is instantaneous.
Overdoped cuprates are an anisotropic marginal Fermi liquid is relevant to his comment about the Anderson-Casey theory of non-Fermi liquid effects.
I welcome further comments.
Glueing together a theory is relevant to his comment about whether the pairing interaction is instantaneous.
Overdoped cuprates are an anisotropic marginal Fermi liquid is relevant to his comment about the Anderson-Casey theory of non-Fermi liquid effects.
I welcome further comments.
Thursday, December 8, 2011
Deconstructing sodium cobaltate
Sodium cobaltate (NaxCoO2) is a strongly correlated electron material which achieved a lot of attention before the mass migration to the new iron pnictide superconductors following their discovery around 2008.
Some of the interest was motivated by the large thermopower, spin frustration associated with the underlying triangular lattice, and superconductivity from water!
Jaime Merino, Ben Powell, and I wrote several papers on the subject. At the cake meeting today we reviewed two papers which focused on the doping x=0.5.
Electronic and magnetic properties of the ionic Hubbard model on the striped triangular lattice at 3/4 filling
Ionic Hubbard model on a triangular lattice for Na0.5CoO2, Rb0.5CoO2, and K0.5CoO2: Mean-field slave boson theory
The latter features some really cool movies.
Here are some of the outstanding questions raised by the strange ground state of the x=0.5 material. It appears to be an insulator, with a small amount of charge order, a large magnetic moment which antiferromagnetically orders, and very small Fermi surface which produces quantum oscillations.
All these properties cannot be described by the strong coupling ground state [an antiferromagnetic insulator with charge order] shown below.
What is the ground state of the ionic Hubbard model on the triangular lattice at 3/4 filling for small Delta/t where Delta=measure of ionicity between the two sublattices?
Is it a covalent insulator? Does such a state have experimental signatures which are distinct from a charge ordered insulator?
How can an "insulating" state co-exist with a very small Fermi surface?
Some of the interest was motivated by the large thermopower, spin frustration associated with the underlying triangular lattice, and superconductivity from water!
Jaime Merino, Ben Powell, and I wrote several papers on the subject. At the cake meeting today we reviewed two papers which focused on the doping x=0.5.
Electronic and magnetic properties of the ionic Hubbard model on the striped triangular lattice at 3/4 filling
Ionic Hubbard model on a triangular lattice for Na0.5CoO2, Rb0.5CoO2, and K0.5CoO2: Mean-field slave boson theory
The latter features some really cool movies.
Here are some of the outstanding questions raised by the strange ground state of the x=0.5 material. It appears to be an insulator, with a small amount of charge order, a large magnetic moment which antiferromagnetically orders, and very small Fermi surface which produces quantum oscillations.
All these properties cannot be described by the strong coupling ground state [an antiferromagnetic insulator with charge order] shown below.
What is the ground state of the ionic Hubbard model on the triangular lattice at 3/4 filling for small Delta/t where Delta=measure of ionicity between the two sublattices?
Is it a covalent insulator? Does such a state have experimental signatures which are distinct from a charge ordered insulator?
How can an "insulating" state co-exist with a very small Fermi surface?
Wednesday, December 7, 2011
A simple concrete proposal to improve the quality of Australian undergraduate education
There is an opinion piece Up-end attendance rules for tutorial and lectures by Peter Van Onselen in the Higher Education Section of today's Australian newspaper. He is a Professor of Political Science at U. of Western Australia and a contributing editor to The Australian. He says that Arts/Humanities courses follow the "tried and true" format of two lectures and one tutorial per week. The former are optional and typically attract less than 50 per cent attendance. Tutorials are compulsory, are over-crowded, and diluted by students who have not done the assigned reading. He argues that the quality of education could be improved, without any additional costs, by making the lectures compulsory and the tutorials optional.
I prefer my own proposals: Fail more students and set the pass rate at the lecture attendance rate.
I prefer my own proposals: Fail more students and set the pass rate at the lecture attendance rate.
Monday, December 5, 2011
Ph.D completion time as a statistical variable
Seth Olsen brought to my attention an article Examining the Relationships among Doctoral Completion Time, Gender, and Future Salary Prospects for Physical Scientists in the Journal of Chemical Education.
It is based on a survey of more than 3000 Ph.D graduates of physics and chemistry in the USA. It claims there is a correlation (for men but not women) between Ph.D completion time and future salary. It also debates whether completion time is a good measure of the scientific merit of the graduate (the shorter the better) and the quality of the program (the longer the better!).
I found I was rather skeptical of many of the claims, values, and assertions in the article. [I also wonder about the reliability of the statistical methodology but am not claiming I could do any better...]. Nevertheless, the article is worth reading because all of the issues it raises and the literature that it surveys.
I welcome any comments on the article.
It is based on a survey of more than 3000 Ph.D graduates of physics and chemistry in the USA. It claims there is a correlation (for men but not women) between Ph.D completion time and future salary. It also debates whether completion time is a good measure of the scientific merit of the graduate (the shorter the better) and the quality of the program (the longer the better!).
I found I was rather skeptical of many of the claims, values, and assertions in the article. [I also wonder about the reliability of the statistical methodology but am not claiming I could do any better...]. Nevertheless, the article is worth reading because all of the issues it raises and the literature that it surveys.
I welcome any comments on the article.
Thursday, December 1, 2011
Optimal doping corresponds to maximum entropy
What is so unique about the optimal doping at which the superconducting transition temperature is a maximum in the cuprates?
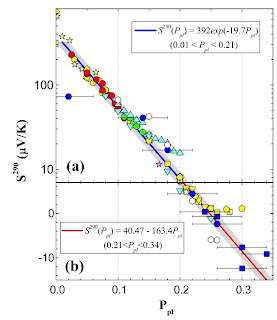
There is an interesting paper Unified electronic phase diagram for hold-doped high-Tc cuprates by Honma and Hor. It builds on their earlier work which argued the existence of a universal planar hole scale (P_pl), which can be characterised by the thermopower at T=290 K, denoted S^290. P_pl is independent of the nature of the dopant, the number of CuO2 plane layers per unit cell, the structure, and the sample quality. The figure below shows S^290 versus P_pl for a wide range of cuprates.
Note that the thermopower changes sign at a doping of P_pl ~ 0.25 which is comparable to that at which Tc is a maximum [except for Sr doped La214].
What is the significance of this sign change of the thermopower?
For a simple Fermi liquid it would correspond to a change in the sign of the charge carriers, i.e., from electrons to holes.
Recently Peterson and Shastry interpreted this sign change in terms of the Kelvin formula for the thermopower, which gives the thermopower as -1/e times the derivative of the entropy with respect to the particle number. This can be related to the temperature dependence of the chemical potential via the Maxwell relation,
Here s=specific entropy, c_h=hole density, mu_h = chemical potential.
It is rather surprising that a transport property can be expressed in terms of a thermodynamic property.
Thus the change in sign of the thermopower means that the entropy is a maximum as a function of hole doping.
Indeed, a maximum in the entropy near optimal doping is was found for the t-J model via
Finite temperature Lanczos calculations on small lattices of up to 20 sites and summarised in a 2000 review by Jaklic and Prelovsek.
The paper also considers a Kelvin type relation for the thermopower, but does not mention Kelvin, and shows how the maximum in the entropy vs. doping is associated with a change in sign of the thermopower.
[Peterson and Shastry do not mention this earlier work.]
A recent preprint by Garg, Shastry, Dave, and Philips, argue that the sign change reflects an underlying quantum critical point at optimal doping. However, I wonder about the extent that one can see a quantum critical effect on lattices as small as 20 sites.
This is related to a 2009 PRB by Mark Jarrell and collaborators who calculated the temperature and doping dependence of the entropy using the cluster dynamical approximation. They found entropy was a maximum at optimal doping [~0.15-0.2]. They also don't mention the earlier work by Jaklic and Prelovsek.
Subscribe to:
Posts (Atom)
Thermodynamics and emergence
Novelty. Temperature and entropy are emergent properties. Classically, they are defined by the zeroth and second laws of thermodynamics, re...
-
Is it something to do with breakdown of the Born-Oppenheimer approximation? In molecular spectroscopy you occasionally hear this term thro...
-
I welcome discussion on this point. I don't think it is as sensitive or as important a topic as the author order on papers. With rega...
-
Nitrogen fluoride (NF) seems like a very simple molecule and you would think it would very well understood, particularly as it is small enou...