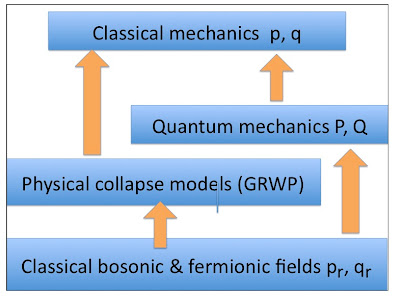
Brain microtubules are not qubits or superconducting!
At the Quantum Theory and Nature of Reality conference on Tuesday night there was an interesting panel discussion with George Ellis , S ir John Polkinghorne , and Sir Roger Penrose. I was surprised and disappointed that Sir Roger Penrose re-iterated the same argument in his book The Emperors New Mind : quantum gravity, the collapse of the wavefunction, and consciousness must all be related. Furthermore, he stood by Hameroff's proposal that a particular type of microtubules are the component with quantum coherence. He mentioned how excited he was about unpublished experimental results of a Japanese group that claim to have measured an electrical resistance of one ohm for microtubules which is comparable to the resistance of the leads. [He seemed to be hinting this implied they were superconducting!]. Why am I so skeptical? See the following: The Penrose-Hameroff Orchestrated Objective-Reduction Proposal for Human Consciousness is Not Biologically Feasible , published in Physic