



What does the scientific community know now that we did not know when you began the research?There is a similar probing question to ask yourself before you start a project (or a new sub-project). Suppose everything goes as well as can be hoped (i.e., you are able to complete the calculation, do the measurement, get the new technique to work, or make the compound). Then will you be able to say something new? If not, is it worth even trying?
"One of the scientific questions I am most interested in is "What is the physical mechanism for XXXX in material YYY? I recently read your nice paper "blah blah" in journal YY and I have been wondering if a similar approach might be relevant to answering my question. I welcome any suggestions from you in this regard....."Dont write:
"Dear Professor,The letter is so important you should spend at least a day writing it, even though is should fit on a single page. Should should get a range of faculty to read it and provide feeback.
I did my Ph.D on topic X and want to continue working on it [even though I have no idea as to whether you have ever worked in this area or have any interest in it]. I published lots of papers [even though most listed on the CV are "in preparation"] and will publish lots more if I come and work with you....]"
 Here are the slides of the fascinating talk that Joel Gilmore gave at the Careers session organised by the Australian Institute of Physics (Qld branch) last wednesday.
Here are the slides of the fascinating talk that Joel Gilmore gave at the Careers session organised by the Australian Institute of Physics (Qld branch) last wednesday.
The chemical capacitance has certain similarities to conventional dielectric capacitance. While the latter is a measure of the ability of the system to store electrical energy in the form of polarized electric dipoles, the former is a measure of the ability of the system to store chemical energy in the form of changes in stoichiometry




“The great power of science is its ability, through brutal objectivity, to reveal to us truth we did not anticipate.”
(p. xvi)
``mythologies are immensely powerful things, and sometimes we humans go to enormous lengths to see the world as we think it should be, even when the evidence says we are mistaken.’’
(p. 114)
“ideologies preclude discovery. All of us see the world as we wish it were rather than as it actually is.”
(p. 116).
There are similarities to the cautions of Walter Kauzmann, in his Reminiscences of a Life in Protein Chemistry.

In a study of 29 graduate students, self-ratings of stress correlated with low scores on self-esteem but were not related to an objective indicator of actual stress. Both self-rated stress and low self-esteem scores were related to scores on depression, with a weak interaction effect.
 Just how efficient are biomolecular systems? For a long time it was claimed that fireflies had a quantum efficiency close to 100 per cent. However, it was recently found this is not the case, the efficiency being about 40%. A nice summary of the work is in this News and Views article in Nature Photonics last year.
Just how efficient are biomolecular systems? For a long time it was claimed that fireflies had a quantum efficiency close to 100 per cent. However, it was recently found this is not the case, the efficiency being about 40%. A nice summary of the work is in this News and Views article in Nature Photonics last year.


The simplest of these problems involve only the spin operators Si of electrons residing on the sites, i, of a regular lattice. Each electron can have its spin oriented either up or down, leading to a Hilbert space of 2N states, on a lattice of N sites. On this space acts the Heisenberg Hamiltonian
H=∑i<j JijSi⋅Sj, (1)where the Jij are a set of short-range exchange interactions, the strongest of which have Jij>0, i.e., are antiferromagnetic. We would like to map the ground-state phase diagram of H as a function of the Jij for a variety of lattices in the limit of N→∞. Note that we are not interested in obtaining the exact wave function of the ground state: this is a hopeless task in dimensions greater than one. Rather, we would be satisfied in a qualitative characterization of each phase in the space of the Jij. Among the possible phases are
(i) a Néel phase, in which the spins have a definite orientation just as in the classical antiferromagnet, with the spin expectation values
all parallel or antiparallel to each other; (ii) a spiral antiferromagnet, which is magnetically ordered like the Néel phase, but the
spins are not collinear; (iii) a valence bond solid (VBS), with the spins paired into S=0 valence bonds, which then crystallize into a preferred arrangement that breaks the lattice symmetry; and
(iv) a spin liquid, with no broken symmetries, neutral S=1/2 elementary excitations, and varieties of a subtle “topological” order.
Specific examples occur for Heisenberg models on the (i) square lattice, (ii), triangular lattice, (iii) kagome lattice (probably).
An example of a model which contains all three is here.
We are still searching for an example of (iv).
 A second issue is how the charge distribution in the molecule changes upon twisting.
A second issue is how the charge distribution in the molecule changes upon twisting.
Almost all modern theoretical chemistry is computational chemistry, because most of the progress that can be made with pencil and paper without a computer has been already made. Computations on complex systems are, in my opinion, the current frontier of theoretical chemistry.I fear this does reflect the view of most in the theoretical chemistry community. However, (as a physicist) I think a much greater emphasis needs to be placed on gaining insights, finding organisation principles, and developing analytical models that complement simulations. But, that is what I am trying to do (and excited about!).
“purely a matter of taste, roughly equivalent to whether or not one believes mathematical language or human language to be more fundamental.”But it is interesting that he is now writing articles about multiverses...

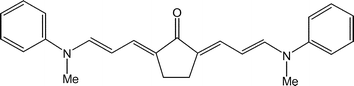
 The description in terms of the three diabatic states allow us to consider a somewhat "generic" or minimal model which exhibits a number of significant features, including:
The description in terms of the three diabatic states allow us to consider a somewhat "generic" or minimal model which exhibits a number of significant features, including: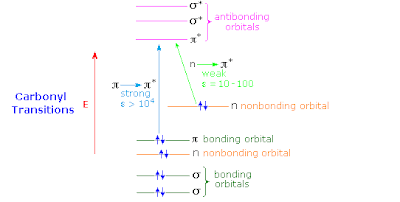








 [Left click to enlarge and make legible.]
[Left click to enlarge and make legible.]Universities and scientific research in the USA are facing a dire future. Understandably, some scientists are considering leaving the USA. I...