Beyond simple molecular orbital theory
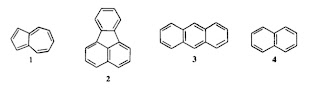
How important are electron-electron interactions in organic molecules? There is a really nice old (1975) paper Why is azulene blue and anthracene white? by Michl and Thulstrup, which highlights the relevant issues. They point out that these two molecules 1 and 3 have similar ionisation energies (IP) and electron afinities (EA) but their lowest lying singlet (S) and triplet (T) excited states have quite different energies (see the Table below). If a simple molecular orbital (Huckel) picture which ignores electron-electron interactions was valid than the energy difference between the LUMO and HOMO would equal IP-EA = T = S. However, the Table clearly shows this is not the case. At the Hartree-Fock level the discrepancies provide a measure of J = Coulomb integral ~ Hubbard U ~ 5 eV 2K= Exchange integral = Singlet-Triplet splitting ~ 1 eV. Michl and Thulstrup give a nice simple explanation of why the exchange integral K is smaller in azulene than in anthracene. (This is what l