Optimal doping corresponds to maximum entropy

What is so unique about the optimal doping at which the superconducting transition temperature is a maximum in the cuprates?

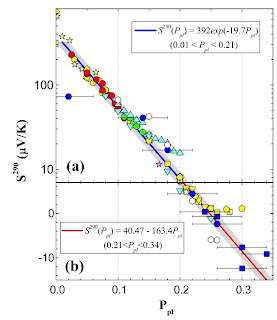
There is an interesting paper Unified electronic phase diagram for hold-doped high-Tc cuprates by Honma and Hor. It builds on their earlier work which argued the existence of a universal planar hole scale (P_pl), which can be characterised by the thermopower at T=290 K, denoted S^290. P_pl is independent of the nature of the dopant, the number of CuO2 plane layers per unit cell, the structure, and the sample quality. The figure below shows S^290 versus P_pl for a wide range of cuprates.

Note that the thermopower changes sign at a doping of P_pl ~ 0.25 which is comparable to that at which  Tc is a maximum [except for Sr doped La214]. 

What is the significance of this sign change of the thermopower?

For a simple Fermi liquid it would correspond to a change in the sign of the charge carriers, i.e., from electrons to holes.

Recently Peterson and Shastry interpreted this sign change in terms of the Kelvin formula for the thermopower, which gives the thermopower as -1/e times the derivative of the entropy with respect to the particle number. This can be related to the temperature dependence of the chemical potential via the Maxwell relation,

Here s=specific entropy, c_h=hole density, mu_h = chemical potential.

It is rather surprising that a transport property can be expressed in terms of a thermodynamic property.

Thus the change in sign of the thermopower means that the entropy is a maximum as a function of hole doping.

Indeed, a maximum in the entropy near optimal doping is was found for the t-J model via 

Finite temperature Lanczos calculations on small lattices of up to 20 sites and summarised in a 2000 review by Jaklic and Prelovsek.

The paper also considers a Kelvin type relation for the thermopower, but does not mention Kelvin, and shows how the maximum in the entropy vs. doping is associated with a change in sign of the thermopower.

[Peterson and Shastry do not mention this earlier work.]

A recent preprint by Garg, Shastry, Dave, and Philips, argue that the sign change reflects an underlying quantum critical point at optimal doping. However, I wonder about the extent that one can see a quantum critical effect on lattices as small as 20 sites. 

This is related to a 2009 PRB by Mark Jarrell and collaborators who calculated the temperature and doping dependence of the entropy using the cluster dynamical approximation. They found entropy was a maximum at optimal doping [~0.15-0.2]. They also don't mention the earlier work by Jaklic and Prelovsek.