Mental health matters

My mental health this year has been up and down. It is not particularly clear why I have struggled at times, given the sources of stress were not particularly bad. Thankfully, now I am the best I have been all year. This may be because I have been quite proactive in taking action. First, there are the basics: adequate sleep, downtime, exercise, and diet. At one point I also cut out all caffeine and alcohol. I also went to the psychologist several times, did more mindfulness exercises, and increased my medication, in consultation with my doctor.

This experience underscores some of the complexities and associated poor understanding of both mental illness and healing. There are biomedical, psychological, social, and spiritual dimensions. There is a high causal density, just like in public policy. Why did I get worse? Why did I get better? As a patient, I don't want to do a series of clinical trials on myself and just change one variable, one after the other. It is better to attack the problem by doing a lot of things that are generally believed to help.

Several people have brought to my attention a series of recent articles in Nature about the mental health of Ph.D. students. These include the following.

Nature’s survey of more than 6,000 graduate students reveals the turbulent nature of doctoral research. 
This stimulated an Editorial,
The mental health of PhD researchers demands urgent attention 
``Anxiety and depression in graduate students is worsening. The health of the next generation of researchers needs systemic change to research cultures.''

Both articles are worth reading, but depressing.

On the one hand, I think it is wonderful Nature is publicising the issue. On the other hand, to me, it is a case of corporate well-washing: where companies pass off responsibility for a problem they have helped create onto their employees or customers. Universities do similar things. If I was asked to name a for-profit company that has a negative influence on ``research culture'' over the past two decades it would be Nature Publishing Group, hands down!

Was Landau the first condensed matter theorist?

Expert readers: please note this post is written for the general audience of a Very Short Introduction. General comments welcome.

Condensed matter physics is not just defined by the objects it studies: condensed states of matter. Rather, the field is also defined by a particular approach. The focus is on finding unifying concepts and organizing principles to address fundamental questions concerning a wide range of phenomena in materials that are chemically and structurally diverse. This approach means looking at the different scales (length, time, and energy) associated with phenomena. In particular, CMP often looks at scales intermediate between the macroscopic and atomic scales. I argued before, that in this sense Kamerlingh Onnes was the first condensed matter experimentalist. In a similar sense, Lev Landau (1908 - 1968) is arguably the first condensed matter theorist, with three papers that he published in 1937, marking the beginning of theoretical CMP.

Landau lived in the Soviet Union and his 1937 papers were almost his last because in 1938 he was arrested for comparing Stalinism to Nazism. The Institute Director, Pyotr Kapitsa, personally wrote to Stalin to no avail. After a year Kapitsa wrote to Molotov (of cocktail fame!), then the nominal head of government, arguing that Landau was indispensable to ``clear up one of the most puzzling areas in modern physics."  In the year following his release Landau developed a theory to explain many of the experiment results on superfluid helium that Kapitsa had obtained. (A nice thank you present!) Landau made notable contributions in all areas of theoretical physics, not just condensed matter. Wikipedia lists more than twenty separate entries describing results, equations, or phenomenon that bear Landau's name. With his former student, Evgeny Lifshitz, Landau co-authored a classic nine-volume series, Course in Theoretical Physics, that is still a standard reference today. Landau also founded a School of Theoretical Physics that produced a plethora of distinguished theoretical physicists. Tragically, Landau’s scientific career ended after a terrible car accident when he was fifty-two years old. He died six years later from injuries associated with the accident. In 1962, Landau was awarded the Nobel Prize in Physics for his work on the theory of superfluidity.

                                              Landau and Kapitsa in 1948.

Landau’s first 1937 paper was concerned with developing the simplest possible theory that could describe the properties of a material near a critical point in the phase diagram, such as associated with a liquid-gas transition or a ferromagnet. A key assumption was that most of the microscopic details, such as the chemical composition of the material, don’t matter much. Landau introduced an order parameter to quantify the amount of ordering present and the symmetry of the ordering. The order parameter varies with temperature and other external parameters such as pressure or magnetic field. It is only non-zero in the ordered state. Landau wrote down the simplest form for the (free) energy of the system as a function of the order parameter. It turns out that symmetry significantly constrains the possible forms for this function. Furthermore, the form is qualitatively different for temperatures above and below the critical temperature. From this simple theory, Landau obtained results for how the order parameter varies with temperature and how there should be a jump (discontinuity) in the specific heat at the critical temperature. What was particularly important was the idea of universality: that most of the microscopic details did not matter and that a wide range of materials and states of matter should have similar properties. Furthermore, the ideas in this paper were foundational for the important ideas about the critical point.

A significant achievement of Landau’s approach to phase transitions was that in 1950, together with Vitaly Ginsburg (1916 - 2009), Landau proposed a theory that could describe many of the properties of superconductors, including how they behaved in the presence of a magnetic field and in thin films. For this work, Ginsburg shared the Nobel Prize in Physics in 2003. Although the Ginzburg-Landau theory could explain a wide range of superconducting phenomena, it left many questions unanswered, including the actual nature and origin of the ordering associated with the superconducting state.

The Ginzburg-Landau theory suggested that the relevant symmetry was a particular symmetry associated with electromagnetism: gauge symmetry. This is a rather abstract concept, but one can give a simple example that may help. With regard to electricity we are familiar with voltage: for example, a 9-volt battery, or a 240-volt appliance. The voltage refers to the electric potential energy; the larger the voltage the stronger the electrical driving force. Voltages are all relative, i.e., they are defined relative to some reference. What is physical is differences in voltage. This is similar to how gravitational potential energy (or elevation) is always defined relative to some reference height, e.g. the floor of the room, sea level, the center of the earth. There is also a gauge symmetry associated with magnetic fields and quantum theory but these are both more complicated and abstract. Later I will discuss experimental manifestations of this breaking of gauge symmetry.

[I am mindful that there are many subtleties about what the ordering and the broken symmetry actually are. For example, this is a breaking of a global gauge symmetry not a local one (which is not allowed by Elitzur's theorem). However, such subtleties are beyond a general audience].

Do you agree that in the sense I discuss Landau was the first condensed matter theorist?
Perhaps it should be van der Waals?

Any corrections?

Any suggestions on how to make this more accessible to a general audience?

Deciding what to do after the thesis

Finishing a thesis (honours, masters, or PhD) can be exhausting: physically, emotionally, and intellectually. When you finally submit it, the last thing you want to do is look at it again or reflect on the experience. Unfortunately, many students do not have a break and soon they are caught up in a job search or starting a new job. Furthermore, it is easy for students to default to the academic track: Masters, PhD, postdoc1, postdoc2, ....

I have posted before about how the privileged few who get tenure may not make the most of transitions within an academic career. Here the focus is on students.

After a well-earned break, it is worth reflecting on the following questions, particularly before deciding what you might do next and how to make that a positive experience.

What are some things you enjoyed? did not enjoy?

What do you think you did well? not well?

What did you learn about yourself, particularly your strengths and weaknesses?

What did you learn about those you worked with: advisors, collaborators, other students, research group members?

If you had your time over again what would you do differently?

Given your answers to all of the above, what does this suggest are some good (bad) options for the future?

Tuning the dimensionality of spin-crossover compounds

An important question concerning spin-crossover compounds concerns the origin and the magnitude of the interactions between the individual molecular units.

There is a nice paper
Evolution of cooperativity in the spin transition of an iron(II) complex on a graphite surface
Lalminthang Kipgen, Matthias Bernien, Sascha Ossinger, Fabian Nickel, Andrew J. Britton, Lucas M. Arruda, Holger Naggert, Chen Luo, Christian Lotze, Hanjo Ryll, Florin Radu, Enrico Schierle, Eugen Weschke, Felix Tuczek, and Wolfgang Kuch

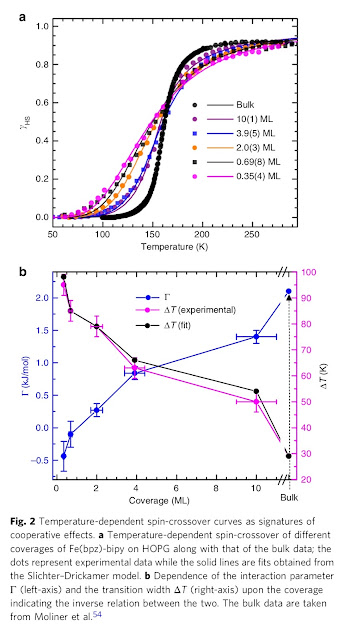
An impressive achievement is the control of the number of monolayers (ML) of SCO molecules deposited on a highly oriented surface pyrolytic graphite. The coverage varies between 0.35 and 10 ML. The shape of the spin-crossover curve changes significantly as the number of monolayers varies, as shown in the upper panel below.

The natural interpretation is that as the number of monolayers increases the interaction between molecules (co-operativity) increases. This can be quantified in terms of the parameter Gamma in the Slichter-Drickamer model [which is equivalent to a mean-field treatment of an Ising model], with Gamma = 4 z J where z=number of nearest-neighbours and J=Ising interaction.
The blue curve in the lower panel shows the variation of Gamma with ML.

The figure above and Table 1 shows that for ML=0.35, Gamma=-0.44 kJ/mol is almost zero for ML=0.7, and then monotonically increases to 2.1 kJ/mol for the bulk.

Does that make sense?

The magnitude of the Gamma values is comparable to those found in other compounds.

The negative value of Gamma for ML=0.35 might be explained as follows. Suppose a monolayer consists of SCO molecules arranged in a square lattice. Then ML=0.33 will consist of chains of SCO molecules that interact in the diagonal direction. If the J_nnn for this next-nearest neighbour interaction is negative then the Gamma value will be negative.

For a monolayer on a square lattice, Gamma= 16 (J_nn + J_nnn). J_nn will be positive and so if it is comparable in magnitude to J_nnn then Gamma will be small for a monolayer.

For a bilayer, Gamma = 16 (J_nn + J_nnn) + 4 J_perp, where J_perp is the interlayer coupling.
For the bulk, Gamma = 16 (J_nn + J_nnn) + 8 J_perp.

This qualitatively explains the trends, but not quantitatively.

The authors also note that the values of Delta E and Delta S obtained from their data vary little with the coverage, as they should since these parameters are single-molecule properties. This also means that the crossover temperature, T_sco also varies little with coverage.

A more rigorous approach is to not use mean-field theory, but rather consider a slab of layers of Ising models. The ratio of the transition temperature T_c to J_nn increases from 2.27 for a single layer to 4.5 as the dimensionality increases from d=2 to d=3.
[In contrast, for mean-field theory the ratio increases from 4 to 6].

If the crossover temperature T_sco is larger than T_c, [as it must be if there is no hysteresis] and assuming J_nn does not change with coverage, then as the coverage increases the crossover temperature becomes closer to the critical temperature and the transition curve will become steeper, reflected in a smaller transition width Delta T (and a correspondingly larger effective Gamma in the Slichter-Drikamer fit). This claim can be understood by looking at the last Figure in this post.

Oral exams need not be like a visit to the dentist

Oral exams (vivas) are quite common for most postgraduate degrees involving research. The basic goal is to provide an efficient mechanism for the examiners to determine a student's level of understanding of what they have done. Most committees comprise both experts and non-experts. Most are actually quite friendly. If the non-experts learn something new they will be happy. Sometimes an examiner may ``grill'' a student simply because they want to understand what is going on. I think the main reason thinks occasionally get tense is when there is a member of the committee who has a poor relationship with the student's advisor or doesn't think much of their research.

To prepare take any opportunity to attend another student's oral exam or ask them about what questions  they were asked and tips.

Some common mistakes that students make are to assume:

Everyone on the committee has read the thesis in detail.

The committee is going to ask highly technical and nuanced questions.

Committee members don't appreciate that I am nervous.

If I can't answer a question it is a disaster.

I should put a positive spin on everything I have done.

Many of the questions asked are usually along the lines of the following.

What is the most important result that you obtained?

How is this work original?

What is the biggest weakness of your approach?

What direction do would you suggest for a student who wishes to build on your work?

What are your plans to publish this work?

Any other suggested advice?

Academic publishing in Majority World

I was asked for an update on this. The challenges are formidable, but not insurmountable.
Here are slides from a talk on the subject.
As always, it is important not to reinvent the wheel.
There are already some excellent resources and organisations. 

A relevant organisation is AuthorAID which is related to inasp, and has online courses on writing. People I know who have taken these courses, or acted as mentors, speak highly of them.

Authors should also make use of software to correct English such as Grammarly.

Publishing Scientific Papers in the Developing World is a helpful book, stemming from a 2010 conference.
Erik Thulstrup has a nice chapter "How should a Young Researcher Write and Publish a Good Research Paper?"

The central role of symmetry in condensed matter

I have now finished my first draft of chapter 3, of Condensed Matter Physics: A Very Short Introduction. 

I welcome comments and suggestions. However, bear in mind my target audience is not the typical reader of this blog, but rather your non-physicist friends and family. 

I think it still needs a lot of work. The goal is for it to be interesting, accessible, and bring out the excitement and importance of condensed matter physics.

This is quite hard work, particularly to try and explain things in an accessible manner.

I am also learning a lot.

I have a couple of basic questions.

How is the symmetry of the rectangular lattice and the centred lattice different?

When was the crystal structure of ice determined by X-ray diffraction?

[Pauling proposed the structure in 1935.]