Emergence? in large language models (revised edition)

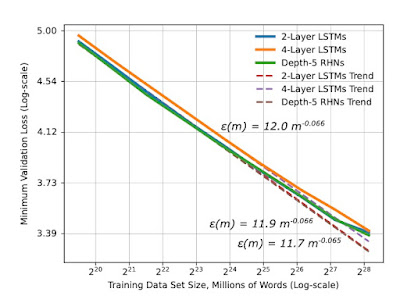
Last year I wrote a post about emergence in AI, specifically on a paper claiming evidence for a "phase transition" in Large Language Models' ability to perform tasks they were not designed for. I found this fascinating.

That paper attracted a lot of attention, even winning an award for the best paper at the conference at which it was presented.

Well, I did not do my homework. Even before my post, another paper called into question the validity of the original paper.

Are Emergent Abilities of Large Language Models a Mirage?

Rylan Schaeffer, Brando Miranda, Sanmi Koyejo

we present an alternative explanation for [the claimed] emergent abilities: that for a particular task and model family, when analyzing fixed model outputs, emergent abilities appear due to the researcher's choice of metric rather than due to fundamental changes in model behavior with scale. Specifically, nonlinear or discontinuous metrics produce apparent emergent abilities, whereas linear or continuous metrics produce smooth, continuous predictable changes in model performance.

... we provide evidence that alleged emergent abilities evaporate with different metrics or with better statistics, and may not be a fundamental property of scaling AI models.

One of the issues they suggest is responsible for the smooth behaviour is 

 the phenomenon known as neural scaling laws: empirical observations that deep networks exhibit power law scaling in the test loss as a function of training dataset size, number of parameters or compute  

One of the papers they cite on power law scaling is below (from 2017).

Deep Learning Scaling is Predictable, Empirically

Joel Hestness, Sharan Narang, Newsha Ardalani, Gregory Diamos, Heewoo Jun, Hassan Kianinejad, Md. Mostofa Ali Patwary, Yang Yang, Yanqi Zhou

The figure below shows the power law scaling between the validation loss and the size of the training data set.

They note that these empirical power laws are yet to be explained.

I thank Gerard Milburn for ongoing discussions about this topic.

Launching my book in a real physical bookshop

Physical bookstores selling physical books are in decline, sadly. Furthermore, the stores that are left are mostly big chains. Brisbane does have an independent bookstore, Avid Reader, in the West End. It is a vibrant part of the local community and has several author events every week.

My daughter persuaded me to do a book launch, for Condensed Matter Physics: A Very Short Introduction (Oxford UP, 2023) 

 

It is at Avid Reader on Monday, February 26, beginning at 6 pm.

Most readers of this blog are not in Brisbane, but if you are or know people who are please encourage them to consider attending.

The event is free but participants need to register, as space is limited.

 

I will be in conversation about the book with my friend, Dr Christian Heim, an author, composer, and psychiatrist. Like the book, the event is meant for a general audience.

  

The role of effective theories and toy models in understanding emergent properties

Two of the approaches to the theoretical description of systems with emergent properties that have been fruitful are effective theories and toy models. These leverage our limited knowledge of many details about a system with many interacting components.

Effective theories

An effective theory is valid at a particular range of scales. This exploits the fact that in complex systems there is often a hierarchy of scales (length, energy, time, or number). In physics, examples of effective theories include classical mechanics, general relativity, classical electromagnetism, and thermodynamics. The equations of an effective theory can be written down almost solely from consideration of symmetry and conservation laws. Examples include the Navier-Stokes equations for fluid dynamics and non-linear sigma models in elementary particle physics. Some effective theories can be derived by the “coarse-graining” of theories that are valid at a finer scale. For example, the equations of classical mechanics result from taking the limit of Planck’s constant going to zero in the equations of quantum mechanics. The Ginzburg-Landau theory for superconductivity can be derived from the BCS theory. The parameters in effective theories may be determined from more microscopic theories or from fitting experimental data to the predictions of the theory. For example, transport coefficients such as conductivities can be calculated from a microscopic theory using a Kubo formula.

Effective theories are useful and powerful because of the minimal assumptions and parameters used in their construction. For the theory to be useful it is not necessary to be able to derive the effective theory from a smaller scale theory, or even to have such a smaller scale theory. For example, even though there is no accepted quantum theory of gravity, general relativity can be used to describe phenomena in astrophysics and cosmology and is accepted to be valid on the macroscopic scale. Some physicists and philosophers may consider smaller-scale theories as more fundamental, but that is contested and so I will not use that language. There also are debates about how effective field theories fit into the philosophy of science.

Toy models

In his 2016 Nobel Lecture, Duncan Haldane said, “Looking back, … I am struck by how important the use of stripped down “toy models” has been in discovering new physics.” 

Here I am concerned with a class of theoretical models that includes the Ising, Hubbard, Agent-Based Models, NK, Schelling, and Sherrington-Kirkpatrick models. I refer to them as “toy” models because they aim to be as simple as possible, while still capturing the essential details of a particular emergent phenomenon. At the scale of interest, the model is an approximation, neglecting certain degrees of freedom and interactions. In contrast, at the relevant scale, effective theories are often considered to be exact because they are based on general principles.

Historical experience has shown that there is a strong justification for the proposal and study of toy models. They are concerned with a qualitative, rather than a quantitative, description of experimental data. A toy model is usually introduced to answer basic questions about what is possible. What are the essential ingredients that are sufficient for an emergent phenomena to occur? What details do matter? For example, the Ising model was introduced in 1920 to see if it was possible for statistical mechanics to describe the sharp phase transition associated with ferromagnetism.  

In his book The Model Thinker and online course Model Thinking, Scott Page has enumerated the value of simple models in the social sciences. An earlier argument for their value in biology was put by JBS Haldane in his seminal article about “bean bag” genetics. Simplicity makes toy models more tractable for mathematical analysis and/or computer simulation. The assumptions made in defining the model can be clearly stated. If the model is tractable then the pure logic associated with mathematical analysis leads to reliable conclusions. This contrasts with the qualitative arguments often used in the biological and social sciences to propose explanations. Such arguments can miss the counter-intuitive conclusions associated with emergent phenomena and the rigorous analysis of toy models. Such models can show what is possible, what are simple ingredients for a system sufficient to exhibit an emergent property, and how a quantitative change can lead to a qualitative change. In different words, what details do matter? 

Toy models can guide what experimental data to gather and how to analyse it. Insight can be gained by considering multiple models as that approach can be used to rule out alternative hypotheses. Finally, there is value in the adage, “all models are wrong, but some are useful.”

Due to universality, sometimes toy models work better than expected, and can even give a quantitative description of experimental data. An example is the three-dimensional Ising model, which was eventually found to be consistent with data on the liquid-gas transition near the critical point. Although, not a magnetic system, the analogy was bolstered by the mapping of the Ising model onto the lattice gas model. This success led to a shift in the attitude of physicists towards the Ising model. According to Martin Niss, from 1920-1950, it was viewed as irrelevant to magnetism because it did not describe magnetic interactions quantum mechanically. This was replaced with the view that it was a model that could give insights into collective phenomena. From 1950-1965, the view diminished that the Ising model was irrelevant to describing critical phenomena because it oversimplified the microscopic interactions.

Physicists are particularly good and experienced at the proposal and analysis of toy models. I think this expertise is a niche that they could exploit more in contributing to other fields, from biology to the social sciences. They just need humility to listen to non-physicists about what the important questions and essential details are.

Four scientific reasons to be skeptical of AI hype

The hype about AI continues, whether in business or science. Undoubtedly, there is a lot of potential in machine learning, big data, and large language models. But that does not mean that the hype is justified. It is more likely to limit real scientific progress and waste a lot of resources.

My innate scepticism receives concrete support from an article from 2018 that gives four scientific reasons for concern.

Big data: the end of the scientific method? 

Sauro Succi and Peter V. Coveney

The article might be viewed as a response to a bizarre article in 2008 by Chris Anderson, editor-in-chief at Wired, The End of Theory: The Data Deluge Makes the Scientific Method Obsolete

‘With enough data, the numbers speak for themselves, correlation replaces causation, and science can advance even without coherent models or unified theories’.

Here are the four scientific reasons for caution about such claims given by Succi and Coveney.

(i) Complex systems are strongly correlated, hence they do not (generally) obey Gaussian statistics.

The law of large numbers (central limit theorem) may not apply and rare events may dominate behaviour. For example, consider the power law decays observed in many complex systems. They are in sharp contrast to the rapid exponential decay in the Gaussian distribution. The authors state, "when rare events are not so rare, convergence rates can be frustratingly slow even in the face of petabytes of data."

(ii) No data are big enough for systems with strong sensitivity to data inaccuracies.

Big data and machine learning involve fitting data to a chosen function, such as a "cost function" with many parameters. That fitting involves a minimisation routine which acts on some sort of "landscape." If the landscape is smooth and minima are well-separated and not separated by too large of maxima then the routine may work. However, if the landscape is rough or the routine gets stuck in some metastable state there will be problems, such as over-fitting.

(iii) Correlation does not imply causation, the link between the two becoming exponentially fainter at increasing data size.  

(iv) In a finite-capacity world, too much data is just as bad as no data.

In other words, it is all about curve fitting. The more parameters used the less likely for insight to be gained. Here the authors quote the famous aphorism, attributed to von Neumann and Fermi, "with four parameters I can fit an elephant and with five I can make his tail wiggle."

Aside: an endearing part of the article is the inclusion of tow choice quotes from C.S. Lewis

‘Once you have surrendered your brain, you've surrendered your life’ (paraphrased)

‘When man proclaims conquest of power of nature, what it really means is conquest of power of some men over other men’.

I commend the article to you and look forward to hearing your perspective. Is the criticism of AI hype fair? Are these four scientific reasons good grounds for concern.