How to finish your Ph.D thesis

Just write it!
Stop procrastinating. Take responsibility.
Don't wait for permission, guidance, or feedback from your supervisor, advisor, committee, or anyone else.
The more you have written and "complete" the greater the pressure on the supervisor, department, and university, to o.k. submission of the thesis.

With supervisors who are tardy/slack/lazy/negligent/disorganised about feedback make sure meetings, submissions of drafts, and requests for feedback are documented in emails.

Another crazy metric?

I have been looking at some books about better writing since next year I am going to be giving a couple of workshops on this. 

I was really intrigued that one book mentioned the Flesch Reading Ease Score which is defined by the equation:

A sign that this is a "widely accepted" metric is that it is incorporated in Microsoft Word.

The main thing that bothers me is the number of significant figures in the coefficients.

But also, surely you could devise the metric so that it actually does give values in the range 0-100, like most guides claim. Pathological text can produces negative values or values greater than 100.

Correlation or causation?

This xkcd cartoon features in an interesting article in the Economist Triumph of the nerds about how the internet has changed the world of cartoons.

Deconstructing excited state dynamics in a solvent

What determines the excited state lifetime of a chromophore in a solvent?
What are the relative importance of the polarity of the solvent [dielectric relaxation time] and the viscosity?

The key physics associated with the solvent polarity is that the dipole moment in the ground and excited states are usually different and so the solvent relaxes and there is an associated redshift of the emission. The viscosity is particularly relevant when there is intramolecular twisting and this motion is usually overdamped.

This problem is of fundamental interest because it concerns overdamped quantum dynamics.
It is of applied interest because significant biomolecular sensors make use of the sensitivity of specific chromophores [e.g. Thioflavin-T binding to amyloid fybrils].

Two recent papers from Dan Huppert's group raise three important questions for me.

An Accounts in Chemical Research
Molecular Rotors: What Lies Behind the High Sensitivity of the Thioflavin-T Fluorescent Marker?
raises the question:
1. What is unique about Thioflavin-T? 
How are the photophysical properties fine tuned?

The authors give convincing arguments as to why Thioflavin-T works. Some of these are reviewed in this earlier post.

However, given there are lots of other chromophores which undergo excited state twisting to dark states [see e.g., this review] it is not clear to me why all these other molecules don't work just as well as Thioflavin-T?

The excited state dynamics is interpreted in terms of the figure below where there are two distinct excited singlet states:

A local excited state (LE) and a twisted intramolecular charge-transfer (TICT) state.

2. Are the LE and TICT states distinct? 

In the simplest two-diabatic state picture there is a single excited state and as the chromophore twists this smoothly evolves from a bright state at the Franck-Condon point to a dark TICT state. This is what Seth Olsen and I found for the chromophore of the Green Fluorescent Protein [see our recent J. Chem. Phys. paper].

The paper
Temperature and Viscosity Dependence of the Nonradiative Decay Rates of Auramine-O and Thioflavin-T in Glass-Forming Solvents
reports that over more than three orders of magnitude the excited state lifetime is proportional to the viscosity and to the dielectric relaxation time.

This raises a subtle issue: causality vs. correlation. The authors point out that in the simple theory of a dielectric liquid the viscosity and the dielectric relaxation time are proportional to one another.

3. Can one separate out the respective contribution of the polarity of the solvent and of the viscosity?

There are two distinct reaction co-ordinates here: the motion associated with each is overdamped. One co-ordinate is the intra-molecular twisting of the solute and which couples to the viscosity of the solvent. The other co-ordinate is the local electric polarisation of the solvent which couples to the dipole moment of the excited state.

Rocket science for children

Yesterday I did some science demos at a kids holiday club, using the Coke-Mentos fountain. Previous efforts led to the post Developing science demonstrations that actually teach science. It is fun and cool to do spectacular demonstrations that cause kids to go "Wow!" and think that science is "fun". But these also need to be a vehicle to teach something about critical thinking and the process of doing science.

Small initiatives can help. For example, I had one child record the height of each of the fountain, that was estimated by the group. This emphasized that measurement, error estimation, record keeping, and comparisons are key parts of doing science.

Aside: Yesterday I thought the Coke-Mentos fountain was higher than last time, particularly for diet Coke. I suspect the fact that is was a hot day helped, increasing the solubility of the carbon dioxide?

We also did Film canister rockets which the kids always enjoy.
I found it amusing that the kids ran off and told their friends they were doing "rocket science".

My questions about condensed phase photochemistry?

For the excited state dynamics of a specific chromophore in a solvent what are the essential degrees of freedom (electronic, vibrational, and solvent) that must be included in a model Hamiltonian?

What determines if the excited state dynamics is classical, semi-classical, or fully quantum? Under what conditions does the Born-Oppenheimer approximation break down?

For a specific photochemical reaction what are the relevant vibrational degrees of freedom? What determines the relative importance of stretching, torsional, and pyramidal vibrations?

What determines the branching ratio for passage through a conical intersection? Relevant parameters may be the slope at the intersection, slanting, size of the wavepacket, and the distance of closest approach (impact parameter)

What is the interplay of the electronic, vibrational and solvent degrees of freedom in excited state dynamics?

What determines the relative importance of the viscosity and the polarity of the solvent for the dynamics? What is the role of the spatial inhomogeneity of the solvent?

In the presence of a solvent what are respective criteria for the localization/delocalization of electronic and/or vibrational excitations over different parts of the chromophore?

What are definitive experimental signatures of delocalization?

What are definitive experimental signatures of breakdown of the Born-Oppenheimer approximation?

What is the role of the solvent in non-adiabatic processes?

Questions about protein folding

What is the physical code that relates the amino acid sequence to a proteins native structure?
How do proteins fold so fast?
Can protein structure be computationally predicted?

These are highlighted as key questions in a nice readable review in Science The Protein Folding problem, 50 years on by Ken Dill and Justin MacCallum.

The article gives a sober assessment of limited but significant achievements and the substantial challenges ahead.

The puzzle of linear magnetoresistance in topological insulators

Tony Wright brought to my attention a nice (brief) review paper on the arXiv
Magnetotransport and induced superconductivity in Bi based three-dimensional topological insulators
M. Veldhorst, M. Snelder, M. Hoek, C. G. Molenaar, D. P. Leusink, A. A. Golubov, H. Hilgenkamp, A. Brinkman
[published version is here].

In passing, I note there is a brief section on Shubnikov de Haas oscillations and the Berry phase. A more extensive discussion can be found in a recent preprint by Tony Wright and I.

Here I briefly discuss the very nice section about linear magnetoresistance (LMR) (i.e. a magnetoresistance that increases linearly with magnetic field, in contrast to the quadratic increase characteristic of regular metals) that have been observed in Bi-based topological insulators. This was of particular interest to me because I previously posted about the puzzle of linear magnetoresistance in Ag2Te [which may or may not be a topological insulator]. Similar issues and theoretical models arise here.

The physical origin of the observed magnetoresistance is also not clear.

First, it is hard to distinguish the contributions from the bulk and the surface conductivity. But, the authors suggest "it seems unlikely that the LMR ... originates from the surface states alone".

Second, the authors raise questions about whether the materials are really in the lowest Landau level, as assumed in Abrikosov's quantum magnetoresistance model. They then critically examine a model by Wang and Lei that requires a linear dispersion and a small Zeeman splitting. This can be distinguished from Abrikosov's model via the density dependence of the LMR.

Two more theoretical models are then discussed.

So, the challenge is to come up with definitive experiments to rule out some of the theories.

I thank Xiaolin Wang for interesting me in this problem last year. His experimental results are reported in this PRL and APL.

A historian on impact factors

Following  my post Impact factors have no impact on me, a question was raised about the role of impact factors in different disciplines and whether they are useful for making comparisons.

Factoring impact describes a history Ph.D student's perspective on first encountering impact factors.

Is ionic polarizability a primary or secondary cause in cuprates?

Distinguishing cause and correlation in complex systems is always a tricky matter.

There is an interesting preprint
Ion-size effects in cuprate superconductors - implications for pairing
B.P.P. Mallett, T. Wolf, E. Gilioli, F. Licci, G.V.M. Williams, A.B. Kaiser, N. Suresh, N.W. Ashcroft, J.L. Tallon

For a large family of cuprates they observe correlations between the basal plane area of the unit cell, the Heisenberg antiferromagnetic exchange J, the maximum superconducting Tc, and the total electric polarizability of the ions.

The main result from this rather impressive systematic study is in the Figure below

The upper graph shows that Tc (max) decreases with increasing J, contrary to what one might expect from spin fluctuation mediated (or RVB) type pictures of superconducitivity (see e.g. this paper which found the pairing amplitude scaled roughly with J).

The lower graph shows that Tc (max) increases with increasing ionic polarizability. The authors then make the claim (first proposed by Neil Ashcroft, one of the authors) that the superconductivity results from pairing via collective excitations of ionic polarizability, rather than via spin fluctuations.

However, I wonder about a different and less radical interpretation.
Assume the maximum Tc does not simply scale with J. One might also worry about what is happening to the tight binding parameter t, since this will also decrease with decreasing unit cell area.

Then remember that the cuprates are charge transfer insulators. The one band t-J model is derived from a two-band model with both p (oxygen) and d (copper) orbitals. The effective J is given by

Background: the figure below taken from this review illustrates the underlying lattice and energy levels.

Hence, as the ions become more polarised the denominator will increase and J will decrease, as is observed here.
Is this less radical hypothesis consistent with the evidence?

Acknowledging a sad reality

Bei-Lok Hu has a nice paper on the arXiv, Emergence: Key physical issues for deeper philosophical inquiries. The acknowledgements end with the poignant (and sad) observation:

 This kind of non mission-driven, non utilitarian work addressing purely intellectual issues is not expected to be supported by any U.S. grant agency.

A key concept in condensed matter: energy scales

To the experienced this post may seem a bit basic but I think it does concern something really important that students must learn and researchers should not forget.
It is a very simple idea but when continually applied it can be quite fruitful. Understanding and teaching condensed matter became a lot easier when I began to appreciate this.

In considering any phenomena in condensed matter it is important to have good estimates (at least within an order of magnitude) of the different energy scales associated with different interactions and effects.

I give several concrete examples to illustrate.

To understand why Fermi liquid theory works so well for elemental metals (sodium, magnesium, tin, ...) the first step is estimating the Fermi energy, the thermal energy (k_B T), the Zeeman energy in a typical laboratory field, ...

A step towards the BCS theory of superconductivity was appreciation of the profound disparity of energy scales, condensation energy much less than k_B T_c comparable to the energy gap, much less than a phonon energy, which in turn is much less than the Fermi energy.
Similarily in the Kondo effect one has the emergence of a low energy scale that is much less than the Fermi energy and the antiferromagnetic Kondo coupling J.

In my own research this issue was a key step in realising that the metallic phase of organic charge transfer salts was a bad metal and could be described by dynamical mean-field theory of the Hubbard model. Specifically it was a puzzle as to why the thermal energy at which the Drude peak disappeared was so much less than the Fermi energy. I first discussed the issues here.

Furthermore, I often find that this simple approach can often rule out exotic phenomena that theorists propose or simplistic explanations that experimentalists make. For example, this post discusses how phenomena discussed in several theory papers require magnetic fields orders of magnitude larger than laboratory fields.

Some may say this skill and approach is important in any area of physics (e.g. fluid dynamics, nuclear physics, optics, ...). However, I suspect it is even more crucial in condensed matter because of the incredible diversity of interactions and emergent phenomena and the associated diversity of energy scales,

Advice to ambitious undergraduates

There is a useful post For the ambitious prospective Ph.D student: a guide.
It is written by Rachael Meager, an undergraduate at Melbourne University, about how Australian students can get into top 10 Economics Ph.D programs, largely in the USA.
Much of the advice is also relevant to science and engineering programs, and I suspect beyond Australia.
It is also relevant to Australian students who want to get a high first class honours result so they can get a Ph.D scholarship within Australia, in a leading research group.

I thought it was cute she recommended writing comments on faculty blogs to make them aware of your existence, interest, and sophistication. Lots of economics faculty write blogs.

In the Australian context I would also suggest that students consider limiting or quitting part-time jobs (McDonald's etc.) unless it is a matter of not eating.
The average Australian undergraduate works something like 10-20 hours per week.
It is simply not possible to do this and expect to have a stellar undergraduate performance.
Take out a student loan or cut back on the i-phone, clubbing, car, overseas holidays....

Having a long commute is also something to avoid.

As usual you have to decide what is really important to you and what short-term sacrifices you are willing to make to achieve long term goals.

BTW: the preceding post on the same economics blog by Rohan Pritchford about the state of "tenure" in Australian universities is also a good read.

What they don't teach you in graduate school

Doug Natelson has a nice post Things no one teaches you as part of your training which discusses some of the crucial skills that scientists (whether university faculty or industrial managers) must have but are never taught.
These include managing people, writing, being a good colleague, ...
The assumption is that these skills are hopefully absorbed by osmosis.
One could argue that they should be more explicitly taught, even if only informally.

One that is particularly important to experimentalists and I had not thought about is managing budgets. Consumables, and equipment purchase and maintenance can easily blow out. If there isn't enough money for these then a lab can grind to a halt.

Some of the comments list useful resources for helping learn some of these skills.

Physical manifestation of the Berry connection

Although I have written several papers about it I still struggle to understand the Berry phase and how it is or may be manifested in solids.
Recent reading, summarised below, has helped.

There is a nice short review Geometry and the anomalous Hall effect in ferromagnets
N. P. Ong and Wei-Li Lee

As late as 1999 Sundaram and Niu wrote down the semi-classical equations of motion for Bloch states in the presence of a Berry curvature, script F below.
(1) and (2) below. n.b. how there is a certain symmetry between x and k.

The last equation gives the "magnetic monopoles" associated with the Berry connection/. Aside: the Berry connection Omega_c is the analogue of the magnetic field. It is related to the curvature F tilde by (F tilde)_ab= epsilon_abc Omega_c.

The Berry connection is related to the Berry phase in the same sense that a magnetic field is associated with an Aharonov-Bohm phase.

The above text is taken from a beautiful paper Berry Curvature on the Fermi Surface: Anomalous Hall Effect as a Topological Fermi-Liquid Property by Duncan Haldane.

The symmetry arguments above show why the anomalous Hall effect only occurs in the presence of time-reversal symmetry breaking, e.g. in a ferromagnet.

It is interesting that Robert Karplus (brother of Martin) and Luttinger wrote down what is now called the Berry connection as long ago as 1954! (30 years before Berry!)
They called it the anomalous velocity.
The connection with Berry and topology was only made in 2002 by Jungwirth, Niu, and MacDonald.
An extensive review of the anomalous Hall effect, both theory and experiment, is here.

A sober critical assessment of computer simulations

There is a nice article on the arXiv, Simulations: the dark side by Daan Frenkel
Here is an extract to give you the flavour

Although this point of view is not universally accepted, scientists are human. Being human, they like to impress their peers. One way to impress your peers is to establish a record. It is for this reason that, year after year, there have been – and will be – claims of the demonstration of ever larger prime numbers: at present – 2012 – the record-holding prime contains more than ten million digits but less than one hundred million digits. As the number of primes is infinite, that search will never end and any record is therefore likely to be overthrown in a relatively short time. No eternal fame there. In simulations, we see a similar effort: the simulation of the ‘largest’ system yet, or the simulation for the longest time yet (it is necessarily ‘either-or’). Again, these records are short-lived. They may be useful to advertise the power of a new computer, but their scientific impact is usually limited.

The article focusses on the technical limitations (and traps) of classical molecular dynamics and Monte Carlo simulations. It would be nice if someone wrote a similar article for quantum simulations.

I learnt of the existence of the article from Doug Natelson's blog, Nanoscale views.

Wilson's ratio for strongly correlated electrons

The (Sommerfeld-)Wilson ratio is an important quantity to characterise strongly correlated Fermi liquids.

Chapter 5 of Hewson's book The Kondo Problem to Heavy Fermions describes the Fermi liquid theory of the Anderson single impurity model. One can derive the identity

which relates the impurity spin susceptibility, charge susceptibility, and the specific heat coefficient gamma.

In the Kondo regime the charge susceptibility is zero and this leads to the fact that the Wilson ratio has the universal value of exactly two.

It is interesting that one can derive the same identity for the exact (Bethe ansatz) solution to the Hubbard model in one dimension. See equation (7) in this paper by Tatsuya Usuki, Norio Kawakami, and Ayao Okiji. As a result one finds the Wilson ratio is always less than 2. As the band filling tends towards one-half the Mott insulator is approached, the charge susceptibility diverges and the Wilson ratio W tends to zero. See the Figure below.

Quantum tunneling changes chemical reactions

The dynamics of the atomic motion associated with most chemical reactions is classical. In particular, the rate of reaction is determined by the rate of thermal excitation over an energy barrier associated with the transition state (a key concept): a particular nuclear configuration which is a saddle point on the potential energy surface which contains both the reactants and products.

It is hard to find exceptions to this paradigm, e.g., where quantum tunneling below the barrier is important. Some people claim this picture breaks down for enzymes, as discussed in an earlier post. But I remain to be convinced, particularly that enzymes have evolved to make use of quantum tunneling.

However, I am convinced and fascinated by an article which does discuss some concrete exceptions to transition state theory for small molecules that have recently been discovered. Tunneling does not just lead to quantitative changes in reaction rates but different products of the chemical reaction.
There is a nice review of this work:

Tunnelling control of chemical reactions – the organic chemist’s perspective
David Ley, Dennis Gerbig and Peter R. Schreiner

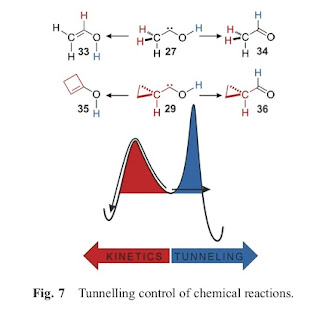
One of the main points is summarised in the figure below. If one starts with the molecule in the centre then at high temperatures the reaction proceeds to the left, because that product involves the lowest energy barrier (activation energy).
However, the energy barrier to produce the molecules shown on the right is narrower. Hence, when the reaction is dominated by tunneling (i.e. at low temperatures) one gets a different product.