According to Wikipedia, "A perverse incentive is an incentive that has an unintended and undesirable result which is contrary to the interests of the incentive makers. Perverse incentives are a type of negative unintended consequence."
There is an excellent (but depressing) article
Academic Research in the 21st Century: Maintaining Scientific Integrity in a Climate of Perverse Incentives and Hypercompetition
Edwards Marc A. and Roy Siddhartha
I learnt of the article via a blog post summarising it, Every attempt to manage academia makes it worse.
Incidentally, Edwards is a water quality expert who was influential in exposing the Flint Water crisis.
The article is particularly helpful because it cites a lot of literature concerning the problems. It contains the following provocative table. I also like the emphasis on ethical behaviour and altruism.
It is easy to feel helpless. However, the least action you can take is to stop looking at metrics when reviewing grants, job applicants, and tenure cases. Actually read some of the papers and evaluate the quality of the science. If you don't have the expertise then you should not be making the decision or should seek expert review.
Thursday, March 30, 2017
Tuesday, March 28, 2017
Computational quantum chemistry in a nutshell
To the uninitiated (and particularly physicists) computational quantum chemistry can just seem to be a bewildering zoo of multiple letter acronyms (CCSD(T), MP4, aug-CC-pVZ, ...).
However, the basic ingredients and key assumptions can be simply explained.
First, one makes the Born-Oppenheimer approximation, i.e. one assumes that the positions of the N_n nuclei in a particular molecule are a classical variable [R is a 3N_n dimensional vector] and the electrons are quantum. One wants to find the eigenenergy of the N electrons. The corresponding Hamiltonian and Schrodinger equation is
The electronic energy eigenvalues E_n(R) define the potential energy surfaces associated with the ground and excited states. From the ground state surface one can understand most of chemistry! (e.g., molecular geometries, reaction mechanisms, transition states, heats of reaction, activation energies, ....)
As Laughlin and Pines say, the equation above is the Theory of Everything!
The problem is that one can't solve it exactly.
Second, one chooses whether one wants to calculate the complete wave function for the electrons or just the local charge density (one-particle density matrix). The latter is what one does in density functional theory (DFT). I will just discuss the former.
Now we want to solve this eigenvalue problem on a computer and the Hilbert space is huge, even for a simple molecule such as water. We want to reduce the problem to a discrete matrix problem. The Hilbert space for a single electron involves a wavefunction in real space and so we want a finite basis set of L spatial wave functions, "orbitals". Then there is the many-particle Hilbert space for N-electrons, which has dimensions of order L^N. We need a judicious way to truncate this and find the best possible orbitals.
The single particle orbitals can be introduced
where the a's are annihilation operators to give the Hamiltonian
These are known as Coulomb and exchange integrals. Sometimes they are denoted (ij|kl).
Computing them efficiently is a big deal.
In semi-empirical theories one neglects many of these integrals and treats the others as parameters that are determined from experiment.
For example, if one only keeps a single term (ii|ii) one is left with the Hubbard model!
Equivalently, the many-particle wave function can be written in this form.
Now one makes two important choices of approximations.
1. atomic basis set
One picks a small set of orbitals centered on each of the atoms in the molecule. Often these have the traditional s-p-d-f rotational symmetry and a Gaussian dependence on distance.
2. "level of theory"
This concerns how one solves the many-body problem or equivalently how one truncates the Hilbert space (electronic configurations) or equivalently uses an approximate variational wavefunction. Examples include Hartree-Fock (HF), second-order perturbation theory (MP2), a Gutzwiller-type wavefunction (CC = Coupled Cluster), or Complete Active Space (CAS(K,L)) (one uses HF for higher and low energies and exact diagonalisation for a small subset of K electrons in L orbitals.
Full-CI (configuration interaction) is exact diagonalisation. This only possible for very small systems.
The many-body wavefunction contains many variational parameters, both the coefficients in from of the atomic orbitals that define the molecular orbitals and the coefficients in front of the Slater determinants that define the electronic configurations.
Obviously, one expects that the larger the atomic basis set and the "higher" the level of theory (i.e. treatment of electron correlation) one hopes to move closer to reality (experiment). I think Pople first drew a diagram such as the one below (taken from this paper).
However, I stress some basic points.
1. Given how severe the truncation of Hilbert space from the original problem one would not necessarily to expect to get anywhere near reality. The pleasant surprise for the founders of the field was that even with 1950s computers one could get interesting results. Although the electrons are strongly correlated (in some sense), Hartree-Fock can sometimes be useful. It is far from obvious that one would expect such success.
2. The convergence to reality is not necessarily uniform.
This gives rise to Pauling points: "improving" the approximation may give worse answers.
3. The relative trade-off between the horizontal and vertical axes is not clear and may be context dependent.
4. Any computational study should have some "convergence" tests. i.e. use a range of approximations and compare the results to see how robust any conclusions are.
However, the basic ingredients and key assumptions can be simply explained.
First, one makes the Born-Oppenheimer approximation, i.e. one assumes that the positions of the N_n nuclei in a particular molecule are a classical variable [R is a 3N_n dimensional vector] and the electrons are quantum. One wants to find the eigenenergy of the N electrons. The corresponding Hamiltonian and Schrodinger equation is
The electronic energy eigenvalues E_n(R) define the potential energy surfaces associated with the ground and excited states. From the ground state surface one can understand most of chemistry! (e.g., molecular geometries, reaction mechanisms, transition states, heats of reaction, activation energies, ....)
As Laughlin and Pines say, the equation above is the Theory of Everything!
The problem is that one can't solve it exactly.
Second, one chooses whether one wants to calculate the complete wave function for the electrons or just the local charge density (one-particle density matrix). The latter is what one does in density functional theory (DFT). I will just discuss the former.
Now we want to solve this eigenvalue problem on a computer and the Hilbert space is huge, even for a simple molecule such as water. We want to reduce the problem to a discrete matrix problem. The Hilbert space for a single electron involves a wavefunction in real space and so we want a finite basis set of L spatial wave functions, "orbitals". Then there is the many-particle Hilbert space for N-electrons, which has dimensions of order L^N. We need a judicious way to truncate this and find the best possible orbitals.
The single particle orbitals can be introduced
where the a's are annihilation operators to give the Hamiltonian
These are known as Coulomb and exchange integrals. Sometimes they are denoted (ij|kl).
Computing them efficiently is a big deal.
In semi-empirical theories one neglects many of these integrals and treats the others as parameters that are determined from experiment.
For example, if one only keeps a single term (ii|ii) one is left with the Hubbard model!
Equivalently, the many-particle wave function can be written in this form.
Now one makes two important choices of approximations.
1. atomic basis set
One picks a small set of orbitals centered on each of the atoms in the molecule. Often these have the traditional s-p-d-f rotational symmetry and a Gaussian dependence on distance.
2. "level of theory"
This concerns how one solves the many-body problem or equivalently how one truncates the Hilbert space (electronic configurations) or equivalently uses an approximate variational wavefunction. Examples include Hartree-Fock (HF), second-order perturbation theory (MP2), a Gutzwiller-type wavefunction (CC = Coupled Cluster), or Complete Active Space (CAS(K,L)) (one uses HF for higher and low energies and exact diagonalisation for a small subset of K electrons in L orbitals.
Full-CI (configuration interaction) is exact diagonalisation. This only possible for very small systems.
The many-body wavefunction contains many variational parameters, both the coefficients in from of the atomic orbitals that define the molecular orbitals and the coefficients in front of the Slater determinants that define the electronic configurations.
Obviously, one expects that the larger the atomic basis set and the "higher" the level of theory (i.e. treatment of electron correlation) one hopes to move closer to reality (experiment). I think Pople first drew a diagram such as the one below (taken from this paper).
However, I stress some basic points.
1. Given how severe the truncation of Hilbert space from the original problem one would not necessarily to expect to get anywhere near reality. The pleasant surprise for the founders of the field was that even with 1950s computers one could get interesting results. Although the electrons are strongly correlated (in some sense), Hartree-Fock can sometimes be useful. It is far from obvious that one would expect such success.
2. The convergence to reality is not necessarily uniform.
This gives rise to Pauling points: "improving" the approximation may give worse answers.
3. The relative trade-off between the horizontal and vertical axes is not clear and may be context dependent.
4. Any computational study should have some "convergence" tests. i.e. use a range of approximations and compare the results to see how robust any conclusions are.
Thursday, March 23, 2017
Units! Units! Units!
I am spending more time with undergraduates lately: helping in a lab (scary!), lecturing, marking assignments, supervising small research projects, ...
One issue keeps coming up: physical units!
Many of the students struggle with this. Some even think it is not important!
This matters in a wide range of activities.
Any others you can think of?
Any thoughts on how we can do better at training students to master this basic but important skill?
One issue keeps coming up: physical units!
Many of the students struggle with this. Some even think it is not important!
This matters in a wide range of activities.
- Giving a meaningful answer for a measurement or calculation. This includes canceling out units.
- Using dimensional analysis to find possible errors in a calculation or formula.
- Writing equations in dimensionless form to simplify calculations, whether analytical or computational.
- Making order of magnitude estimates of physical effects.
Any others you can think of?
Any thoughts on how we can do better at training students to master this basic but important skill?
Tuesday, March 21, 2017
Emergence frames many of the grand challenges and big questions in universities
What are the big questions that people are (or should be) wrestling within universities?
What are the grand intellectual challenges, particularly those that interact with society?
Here are a few. A common feature of those I have chosen is that they involve emergence: complex systems consisting of many interacting components produce new entities and there are multiple scales (whether length, time, energy, the number of entities) involved.
Economics
How does one go from microeconomics to macroeconomics?
What is the interaction between individual agents and the surrounding economic order?
A recent series of papers(see here and references therein) have looked at how the concept of emergence played a role in the thinking of Friedrich Hayek.
Biology
How does one go from genotype to phenotype?
How do the interactions between many proteins produce a biochemical process in a cell?
The figure above shows a protein interaction network and taken from this review.
Sociology
How do communities and cultures emerge?
What is the relationship between human agency and social structures?
Public health and epidemics
How do diseases spread and what is the best strategy to stop them?
Computer science
Artificial intelligence.
Recently it was shown how Deep learning can be understood in terms of the renormalisation group.
Community development, international aid, and poverty alleviation
I discussed some of the issues in this post.
Intellectual history
How and when do new ideas become "popular" and accepted?
Climate change
Philosophy
How do you define consciousness?
Some of the issues are covered in the popular book, Emergence: the connected lives of Ants, Brains, Cities, and Software.
Some of these phenomena are related to the physics of networks, including scale-free networks. The most helpful introduction I have read is a Physics Today article by Mark Newman.
Given this common issue of emergence, I think there are some lessons (and possibly techniques) these fields might learn from condensed matter physics. It is arguably the field which has been the most successful at understanding and describing emergent phenomena. I stress that this is not hubris. This success is not because condensed matter theorists are smarter or more capable than people working in other fields. It is because the systems are "simple" enough and the presence (sometimes) of a clear separation of scales that they are more amenable to analysis and controlled experiments.
Some of these lessons are "obvious" to condensed matter physicists. However, I don't think they are necessarily accepted by researchers in other fields.
Humility.
These are very hard problems, progress is usually slow, and not all questions can be answered.
The limitations of reductionism.
Trying to model everything by computer simulations which include all the degrees of freedom will lead to limited progress and insight.
Find and embrace the separation of scales.
The renormalisation group provides a method to systematically do this. A recent commentary by Ilya Nemenman highlights some recent progress and the associated challenges.
The centrality of concepts.
The importance of critically engaging with experiment and data.
They must be the starting and end point. Concepts, models, and theories have to be constrained and tested by reality.
The value of simple models.
They can give significant insight into the essentials of a problem.
What other big questions and grand challenges involve emergence?
Do you think condensed matter [without hubris] can contribute something?
What are the grand intellectual challenges, particularly those that interact with society?
Here are a few. A common feature of those I have chosen is that they involve emergence: complex systems consisting of many interacting components produce new entities and there are multiple scales (whether length, time, energy, the number of entities) involved.
Economics
How does one go from microeconomics to macroeconomics?
What is the interaction between individual agents and the surrounding economic order?
A recent series of papers(see here and references therein) have looked at how the concept of emergence played a role in the thinking of Friedrich Hayek.
Biology
How does one go from genotype to phenotype?
How do the interactions between many proteins produce a biochemical process in a cell?
The figure above shows a protein interaction network and taken from this review.
Sociology
How do communities and cultures emerge?
What is the relationship between human agency and social structures?
Public health and epidemics
How do diseases spread and what is the best strategy to stop them?
Computer science
Artificial intelligence.
Recently it was shown how Deep learning can be understood in terms of the renormalisation group.
Community development, international aid, and poverty alleviation
I discussed some of the issues in this post.
Intellectual history
How and when do new ideas become "popular" and accepted?
Climate change
Philosophy
How do you define consciousness?
Some of the issues are covered in the popular book, Emergence: the connected lives of Ants, Brains, Cities, and Software.
Some of these phenomena are related to the physics of networks, including scale-free networks. The most helpful introduction I have read is a Physics Today article by Mark Newman.
Some of these lessons are "obvious" to condensed matter physicists. However, I don't think they are necessarily accepted by researchers in other fields.
Humility.
These are very hard problems, progress is usually slow, and not all questions can be answered.
The limitations of reductionism.
Trying to model everything by computer simulations which include all the degrees of freedom will lead to limited progress and insight.
Find and embrace the separation of scales.
The renormalisation group provides a method to systematically do this. A recent commentary by Ilya Nemenman highlights some recent progress and the associated challenges.
The centrality of concepts.
The importance of critically engaging with experiment and data.
They must be the starting and end point. Concepts, models, and theories have to be constrained and tested by reality.
The value of simple models.
They can give significant insight into the essentials of a problem.
What other big questions and grand challenges involve emergence?
Do you think condensed matter [without hubris] can contribute something?
Saturday, March 18, 2017
Important distinctions in the debate about journals
My post, "Do we need more journals?" generated a lot of comments, showing that the associated issues are something people have strong opinions about.
I think it important to consider some distinct questions that the community needs to debate.
What research fields, topics, and projects should we work on?
When is a specific research result worth communicating to the relevant research community?
Who should be co-authors of that communication?
What is the best method of communicating that result to the community?
How should the "performance" and "potential" of individuals, departments, and institutions be evaluated?
A major problem for science is that over the past two decades the dominant answer to the last question (metrics such as Journal "Impact" Factors and citations) is determining the answer to the other questions. This issue has been nicely discussed by Carl Caves.
The tail is wagging the dog.
People flock to "hot" topics that can produce quick papers, may attract a lot of citations, and are beloved by the editors of luxury journals. Results are often obtained and analysed in a rush, not checked adequately, and presented in the "best" possible light with a bias towards exotic explanations. Co-authors are sometimes determined by career issues and the prospect of increasing the probability of publication in a luxury journal, rather than by scientific contribution.
Finally, there is a meta-question that is in the background. The question is actually more important but harder to answer.
How are the answers to the last question being driven by broader moral and political issues?
Examples include the rise of the neoliberal management class, treatment of employees, democracy in the workplace, inequality, post-truth, the value of status and "success", economic instrumentalism, ...
I think it important to consider some distinct questions that the community needs to debate.
What research fields, topics, and projects should we work on?
When is a specific research result worth communicating to the relevant research community?
Who should be co-authors of that communication?
What is the best method of communicating that result to the community?
How should the "performance" and "potential" of individuals, departments, and institutions be evaluated?
A major problem for science is that over the past two decades the dominant answer to the last question (metrics such as Journal "Impact" Factors and citations) is determining the answer to the other questions. This issue has been nicely discussed by Carl Caves.
The tail is wagging the dog.
People flock to "hot" topics that can produce quick papers, may attract a lot of citations, and are beloved by the editors of luxury journals. Results are often obtained and analysed in a rush, not checked adequately, and presented in the "best" possible light with a bias towards exotic explanations. Co-authors are sometimes determined by career issues and the prospect of increasing the probability of publication in a luxury journal, rather than by scientific contribution.
Finally, there is a meta-question that is in the background. The question is actually more important but harder to answer.
How are the answers to the last question being driven by broader moral and political issues?
Examples include the rise of the neoliberal management class, treatment of employees, democracy in the workplace, inequality, post-truth, the value of status and "success", economic instrumentalism, ...
Thursday, March 16, 2017
Introducing students to John Bardeen
At UQ there is a great student physics club, PAIN. Their weekly meeting is called the "error bar." This friday they are having a session on the history of physics and asked faculty if any would talk "about interesting stories or anecdotes about people, discoveries, and ideas relating to physics."
Here are my slides.
In preparing the talk I read the interesting articles in the April 1992 issue of Physics Today that was completely dedicated to Bardeen. In his article David Pines, says
I thought for a while and decided on John Bardeen. There is a lot I find interesting. He is the only person to receive two Nobel Prizes in Physics. Arguably, the discovery associated with both prizes (transistor, BCS theory) are of greater significance than the average Nobel. The difficult relationship with Shockley, who in some sense became the founder of Silicon Valley.
Here are my slides.
In preparing the talk I read the interesting articles in the April 1992 issue of Physics Today that was completely dedicated to Bardeen. In his article David Pines, says
[Bardeen's] approach to scientific problems went something like this:
- Focus first on the experimental results, by careful reading of the literature and personal contact with members of leading experimental groups.
- Develop a phenomenological description that ties the key experimental facts together.
- Avoid bringing along prior theoretical baggage, and do not insist that a phenomenological description map onto a particular theoretical model. Explore alternative physical pictures and mathematical descriptions without becoming wedded to a specific theoretical approach.
- Use thermodynamic and macroscopic arguments before proceeding to microscopic calculations.
- Focus on physical understanding, not mathematical elegance. Use the simplest possible mathematical descriptions.
- Keep up with new developments and techniques in theory, for one of these could prove useful for the problem at hand.
- Don't give up! Stay with the problem until it's solved.
In summary, John believed in a bottom-up, experimentally based approach to doing physics, as distinguished from a top-down, model-driven approach. To put it another way, deciding on an appropriate model Hamiltonian was John's penultimate step in solving a problem, not his first.With regard to "interesting stories or anecdotes about people, discoveries, and ideas relating to physics," what would you talk about?
Wednesday, March 15, 2017
The power and limitations of ARPES
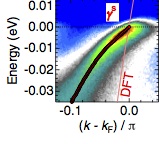
The past two decades have seen impressive advances in Angle-Resolved PhotoEmission Spectroscopy (ARPES). This technique has played a particularly important role in elucidating the properties of the cuprates and topological insulators. ARPES allows measurement of the one-electron spectral function, A(k,E) something that can be calculated from quantum many-body theory. Recent advances have included the development of laser-based ARPES, which makes synchrotron time unnecessary.
A recent PRL shows the quality of data that can be achieved.
Orbital-Dependent Band Narrowing Revealed in an Extremely Correlated Hund’s Metal Emerging on the Topmost Layer of Sr2RuO4
Takeshi Kondo, M. Ochi, M. Nakayama, H. Taniguchi, S. Akebi, K. Kuroda, M. Arita, S. Sakai, H. Namatame, M. Taniguchi, Y. Maeno, R. Arita, and S. Shin
The figure below shows a colour density plot of the intensity [related to A(k,E)] along a particular direction in the Brillouin zone. The energy resolution is of the order of meV, something that would not have been dreamed of decades ago.
Note how the observed dispersion of the quasi-particles is much smaller than that calculated from DFT, showing how strongly correlated the system is.
The figure below shows how with increasing temperature a quasi-particle peak gradually disappears, showing the smooth crossover from a Fermi liquid to a bad metal, above some coherence temperature.
The main point of the paper is that the authors are able to probe just the topmost layer of the crystal and that the associated electronic structure is more correlated (the bands are narrower and the coherence temperature is lower) than the bulk.
Again it is impressive that one can make this distinction.
But this does highlight a limitation of ARPES, particularly in the past. It is largely a surface probe and so one has to worry about whether one is measuring surface properties that are different from the bulk. This paper shows that those differences can be significant.
The paper also contains DFT+DMFT calculations which are compared to the experimental results.
A recent PRL shows the quality of data that can be achieved.
Orbital-Dependent Band Narrowing Revealed in an Extremely Correlated Hund’s Metal Emerging on the Topmost Layer of Sr2RuO4
Takeshi Kondo, M. Ochi, M. Nakayama, H. Taniguchi, S. Akebi, K. Kuroda, M. Arita, S. Sakai, H. Namatame, M. Taniguchi, Y. Maeno, R. Arita, and S. Shin
The figure below shows a colour density plot of the intensity [related to A(k,E)] along a particular direction in the Brillouin zone. The energy resolution is of the order of meV, something that would not have been dreamed of decades ago.
Note how the observed dispersion of the quasi-particles is much smaller than that calculated from DFT, showing how strongly correlated the system is.
The figure below shows how with increasing temperature a quasi-particle peak gradually disappears, showing the smooth crossover from a Fermi liquid to a bad metal, above some coherence temperature.
The main point of the paper is that the authors are able to probe just the topmost layer of the crystal and that the associated electronic structure is more correlated (the bands are narrower and the coherence temperature is lower) than the bulk.
Again it is impressive that one can make this distinction.
But this does highlight a limitation of ARPES, particularly in the past. It is largely a surface probe and so one has to worry about whether one is measuring surface properties that are different from the bulk. This paper shows that those differences can be significant.
The paper also contains DFT+DMFT calculations which are compared to the experimental results.
Monday, March 13, 2017
What do your students really expect and value?
Should you ban cell phones in class?
I found this video quite insightful. It reminded me of the gulf between me and some students.
It confirmed my policy of not allowing texting in class. Partly this is to force students to be more engaged. But it is also to make students think about whether they really need to be "connected" all the time?
What is your policy of phones in class?
I think that the characterisation of "millennials" may be a bit harsh and too one dimensional. Although I did encounter some of the underlying attitudes in a problematic class a few years ago. Then reading a Time magazine cover article was helpful.
I also think that this is not a good characterisation of many of the students that make it as far as an advanced undergraduate or Ph.D programs. By then many of the narcissistic and entitled have self selected out. It is just too much hard work.
I found this video quite insightful. It reminded me of the gulf between me and some students.
It confirmed my policy of not allowing texting in class. Partly this is to force students to be more engaged. But it is also to make students think about whether they really need to be "connected" all the time?
What is your policy of phones in class?
I think that the characterisation of "millennials" may be a bit harsh and too one dimensional. Although I did encounter some of the underlying attitudes in a problematic class a few years ago. Then reading a Time magazine cover article was helpful.
I also think that this is not a good characterisation of many of the students that make it as far as an advanced undergraduate or Ph.D programs. By then many of the narcissistic and entitled have self selected out. It is just too much hard work.
Friday, March 10, 2017
Do we really need more journals?
NO!
Nature Publishing Group continues to spawn "Baby Natures" like crazy.
I was disappointed to see that Physical Review is launching a new journal Physical Review Materials. They claim it is to better serve the materials community. I found this strange. What is wrong with Physical Review B? It does a great job.
Surely, the real reason is APS wants to compete with Nature Materials [a front for mediocrity and hype] which has a big Journal Impact Factor (JIF).
On the other hand, if the new journal could put Nature Materials out of business I would be very happy. At least the journal would be run and controlled by real scientists and not-for-profit.
So I just want to rant two points I have made before.
First, the JIF is essentially meaningless, particularly when it comes to evaluating the quality of individual papers. Even if one believes citations are some sort of useful measure of impact, one should look at the distribution, not just the mean. Below the distribution is shown for Nature Chemistry.
Note how the distribution is highly skewed, being dominated by a few highly cited papers. More than 70 per cent of papers score less than the mean.
Second, the problem is that people are publishing too many papers. We need less journals not more!
Three years ago, I posted about how I think journals are actually redundant and gave a specific proposal of how to move towards a system that produces better science (more efficiently) and more accurately evaluates the quality of individuals contributions.
Getting there will obviously be difficult. However, initiatives such as SciPost and PLOS ONE, are steps in a positive direction.
Meanwhile those of us evaluating the "performance" of individuals can focus on real science and not all this nonsense beloved by many.
Nature Publishing Group continues to spawn "Baby Natures" like crazy.
I was disappointed to see that Physical Review is launching a new journal Physical Review Materials. They claim it is to better serve the materials community. I found this strange. What is wrong with Physical Review B? It does a great job.
Surely, the real reason is APS wants to compete with Nature Materials [a front for mediocrity and hype] which has a big Journal Impact Factor (JIF).
On the other hand, if the new journal could put Nature Materials out of business I would be very happy. At least the journal would be run and controlled by real scientists and not-for-profit.
So I just want to rant two points I have made before.
First, the JIF is essentially meaningless, particularly when it comes to evaluating the quality of individual papers. Even if one believes citations are some sort of useful measure of impact, one should look at the distribution, not just the mean. Below the distribution is shown for Nature Chemistry.
Note how the distribution is highly skewed, being dominated by a few highly cited papers. More than 70 per cent of papers score less than the mean.
Second, the problem is that people are publishing too many papers. We need less journals not more!
Three years ago, I posted about how I think journals are actually redundant and gave a specific proposal of how to move towards a system that produces better science (more efficiently) and more accurately evaluates the quality of individuals contributions.
Getting there will obviously be difficult. However, initiatives such as SciPost and PLOS ONE, are steps in a positive direction.
Meanwhile those of us evaluating the "performance" of individuals can focus on real science and not all this nonsense beloved by many.
Wednesday, March 8, 2017
Is complexity theory relevant to poverty alleviation programs?
For me, global economic inequality is a huge issue. A helpful short video describes the problem.
Recently, there has been a surge of interest among development policy analysts about how complexity theory may be relevant in poverty alleviation programs.
On an Oxfam blog there is a helpful review of three books on complexity theory and development.
I recently read some of one of these books, Aid on the Edge of Chaos: Rethinking International Cooperation in a Complex World, by Ben Ramalingham.
Here is some of the publisher blurb.
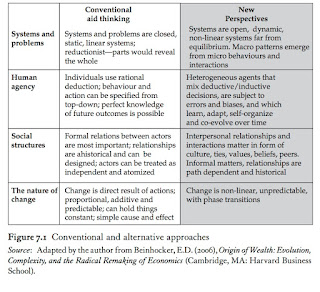
The Table below nicely contrasts two approaches.
A friend who works for a large aid NGO told me about the book and described a workshop (based on the book) that he attended where the participants even used modeling software.
I have mixed feelings about all of this.
Here are some positive points.
Any problem in society involves a complex system (i.e. many interacting components). Insights, both qualitative and quantitative, can be gained from "physics" type models. Examples I have posted about before, include the statistical mechanics of money and the universality in probability distributions for certain social quantities.
Simplistic mechanical thinking, such as that associated with Robert McNamara in Vietnam and then at the World Bank, is problematic and needs to be critiqued. Even a problem as 'simple" as replacing wood burning stoves turns out to be much more difficult and complicated than anticipated.
A concrete example discussed in the book is that of positive deviance, which takes its partial motivation from power laws.
Here are some concerns.
Complexity theory suffers from being oversold. It certainly gives important qualitative insights and concrete examples in "simple" models. However, to what extent complexity theory can give a quantitative description of real systems is debatable. This is particularly true of the idea of "the edge of chaos" that features in the title of the book. A less controversial title would have replaced this with simply "emergence", since that is a lot of what the book is really about.
Some of the important conclusions of the book could be arrived at by different more conventional routes. For example, a major point is that "top down" approaches are problematic. This is where some wealthy Westerners define a problem, define the solution, then provide the resources (money, materials, and personnel) and impose the solution on local poor communities. A more "bottom up" or "complex adaptive systems" approach is where one consults with the community, gets them to define the problem and brainstorm possible solutions, give them ownership of implementing the project, and adapt the strategy in response to trials. One can come to this same approach if ones starting point is simply humility and respect for the dignity of others. We don't need complexity theory for that.
The author makes much of the story of Sugata Mitra, whose TED talk, "Kids can teach themselves" has more than a million views. He puts some computer terminals in a slum in India and claims that poor uneducated kids taught themselves all sorts of things, illustrating "emergent" and "bottom up" solutions. It is a great story. However, it has received some serious criticism, which is not acknowledged by the author.
Nevertheless, I recommend the book and think it is a valuable and original contribution about a very important issue.
Recently, there has been a surge of interest among development policy analysts about how complexity theory may be relevant in poverty alleviation programs.
On an Oxfam blog there is a helpful review of three books on complexity theory and development.
I recently read some of one of these books, Aid on the Edge of Chaos: Rethinking International Cooperation in a Complex World, by Ben Ramalingham.
Here is some of the publisher blurb.
Ben Ramalingam shows that the linear, mechanistic models and assumptions on which foreign aid is built would be more at home in early twentieth century factory floors than in the dynamic, complex world we face today. All around us, we can see the costs and limitations of dealing with economies and societies as if they are analogous to machines. The reality is that such social systems have far more in common with ecosystems: they are complex, dynamic, diverse and unpredictable.
Many thinkers and practitioners in science, economics, business, and public policy have started to embrace more 'ecologically literate' approaches to guide both thinking and action, informed by ideas from the 'new science' of complex adaptive systems. Inspired by these efforts, there is an emerging network of aid practitioners, researchers, and policy makers who are experimenting with complexity-informed responses to development and humanitarian challenges.
This book showcases the insights, experiences, and often remarkable results from these efforts. From transforming approaches to child malnutrition, to rethinking processes of economic growth, from building peace to combating desertification, from rural Vietnam to urban Kenya, Aid on the Edge of Chaos shows how embracing the ideas of complex systems thinking can help make foreign aid more relevant, more appropriate, more innovative, and more catalytic. Ramalingam argues that taking on these ideas will be a vital part of the transformation of aid, from a post-WW2 mechanism of resource transfer, to a truly innovative and dynamic form of global cooperation fit for the twenty-first century.The first few chapters give a robust and somewhat depressing critique of the current system of international aid. He then discusses complexity theory and finally specific case studies.
The Table below nicely contrasts two approaches.
A friend who works for a large aid NGO told me about the book and described a workshop (based on the book) that he attended where the participants even used modeling software.
I have mixed feelings about all of this.
Any problem in society involves a complex system (i.e. many interacting components). Insights, both qualitative and quantitative, can be gained from "physics" type models. Examples I have posted about before, include the statistical mechanics of money and the universality in probability distributions for certain social quantities.
Simplistic mechanical thinking, such as that associated with Robert McNamara in Vietnam and then at the World Bank, is problematic and needs to be critiqued. Even a problem as 'simple" as replacing wood burning stoves turns out to be much more difficult and complicated than anticipated.
A concrete example discussed in the book is that of positive deviance, which takes its partial motivation from power laws.
Here are some concerns.
Complexity theory suffers from being oversold. It certainly gives important qualitative insights and concrete examples in "simple" models. However, to what extent complexity theory can give a quantitative description of real systems is debatable. This is particularly true of the idea of "the edge of chaos" that features in the title of the book. A less controversial title would have replaced this with simply "emergence", since that is a lot of what the book is really about.
Some of the important conclusions of the book could be arrived at by different more conventional routes. For example, a major point is that "top down" approaches are problematic. This is where some wealthy Westerners define a problem, define the solution, then provide the resources (money, materials, and personnel) and impose the solution on local poor communities. A more "bottom up" or "complex adaptive systems" approach is where one consults with the community, gets them to define the problem and brainstorm possible solutions, give them ownership of implementing the project, and adapt the strategy in response to trials. One can come to this same approach if ones starting point is simply humility and respect for the dignity of others. We don't need complexity theory for that.
The author makes much of the story of Sugata Mitra, whose TED talk, "Kids can teach themselves" has more than a million views. He puts some computer terminals in a slum in India and claims that poor uneducated kids taught themselves all sorts of things, illustrating "emergent" and "bottom up" solutions. It is a great story. However, it has received some serious criticism, which is not acknowledged by the author.
Nevertheless, I recommend the book and think it is a valuable and original contribution about a very important issue.
Monday, March 6, 2017
A dirty secret in molecular biophysics
The past few decades has seen impressive achievements in molecular biophysics that are based on two techniques that are now common place.
Using X-ray crystallography to determine the detailed atomic structure of proteins.
Classical molecular dynamics simulations.
However, there is a fact that is not as widely known and acknowledged as it should be. These two complementary techniques have an unhealthy symbiotic relationship.
Protein crystal structures are often "refined" using molecular dynamics simulations.
The "force fields" used in the simulations are often parametrised using known crystal structures!
There are at least two problems with this.
1. Because the methods are not independent of one another one cannot claim that a because in a particular case they give the same result that one has achieved something, particularly "confirmation" of the validity of a result.
2. Classical force fields are classical and do not necessarily give a good description of the finer details of chemical bonding, something that is intrinsically quantum mechanical. The active sites of proteins are "special" by definition. They are finely tuned to perform a very specific biomolecular function (e.g. catalysis of a specific chemical reaction or conversion of light into electrical energy). This is particularly true of hydrogen bonds, where bond length differences of less than a 1/20 of an Angstrom can make a huge difference to a potential energy surface.
I don't want to diminish or put down the great achievements of these two techniques. We just need to be honest and transparent about their limitations and biases.
I welcome comments.
Using X-ray crystallography to determine the detailed atomic structure of proteins.
Classical molecular dynamics simulations.
However, there is a fact that is not as widely known and acknowledged as it should be. These two complementary techniques have an unhealthy symbiotic relationship.
Protein crystal structures are often "refined" using molecular dynamics simulations.
The "force fields" used in the simulations are often parametrised using known crystal structures!
There are at least two problems with this.
1. Because the methods are not independent of one another one cannot claim that a because in a particular case they give the same result that one has achieved something, particularly "confirmation" of the validity of a result.
2. Classical force fields are classical and do not necessarily give a good description of the finer details of chemical bonding, something that is intrinsically quantum mechanical. The active sites of proteins are "special" by definition. They are finely tuned to perform a very specific biomolecular function (e.g. catalysis of a specific chemical reaction or conversion of light into electrical energy). This is particularly true of hydrogen bonds, where bond length differences of less than a 1/20 of an Angstrom can make a huge difference to a potential energy surface.
I don't want to diminish or put down the great achievements of these two techniques. We just need to be honest and transparent about their limitations and biases.
I welcome comments.
Friday, March 3, 2017
Science is told by the victors and Learning to build models
A common quote about history is that "History is written by the victors". The over-simplified point is that sometimes the losers of a war are obliterated (or at least lose power) and so don't have the opportunity to tell their side of the story. In contrast, the victors want to propagate a one-sided story about their heroic win over their immoral adversaries. The origin of this quote is debatable but there is certainly a nice article where George Orwell discusses the problem in the context of World War II.
What does this have to do with teaching science?
The problem is that textbooks present nice clean discussions of successful theories and models that rarely engage with the complex and tortuous path that was taken to get to the final version.
If the goal is "efficient" learning and minimisation of confusion this is appropriate.
However, we should ask whether this is the best way for students to actually learn how to DO and understand science.
I have been thinking about this because this week I am teaching the Drude model in my solid state physics course. Because of its simplicity and success, it is an amazing and beautiful theory. But, it is worth thinking about two key steps in constructing the model; steps that are common (and highly non-trivial) in constructing any theoretical model in science.
1. Deciding which experimental observables and results one wants to describe.
2. Deciding which parameters or properties will be ingredients of the model.
For 1. it is Ohm's law, Fourier's law, Hall effect, Drude peak, UV transparency of metals, Weidemann-Franz, magnetoresistance, thermoelectric effect, specific heat, ...
For 2. one starts with only conduction electrons (not valence electrons or ions), no crystal structure or chemical detail (except valence), and focuses on averages (velocity, scattering time, density) rather than standard deviations, ...
In hindsight, it is all "obvious" and "reasonable" but spare a thought for Drude in 1900. It was only 3 years after the discovery of the electron, before people were even certain that atoms existed, and certainly before the Bohr model...
This issue is worth thinking about as we struggle to describe and understand complex systems such as society, the economy, or biological networks. One can nicely see 1. and 2. above in a modest and helpful article by William Bialek, Perspectives on theory at the interface of physics and biology.
What does this have to do with teaching science?
The problem is that textbooks present nice clean discussions of successful theories and models that rarely engage with the complex and tortuous path that was taken to get to the final version.
If the goal is "efficient" learning and minimisation of confusion this is appropriate.
However, we should ask whether this is the best way for students to actually learn how to DO and understand science.
I have been thinking about this because this week I am teaching the Drude model in my solid state physics course. Because of its simplicity and success, it is an amazing and beautiful theory. But, it is worth thinking about two key steps in constructing the model; steps that are common (and highly non-trivial) in constructing any theoretical model in science.
1. Deciding which experimental observables and results one wants to describe.
2. Deciding which parameters or properties will be ingredients of the model.
For 1. it is Ohm's law, Fourier's law, Hall effect, Drude peak, UV transparency of metals, Weidemann-Franz, magnetoresistance, thermoelectric effect, specific heat, ...
For 2. one starts with only conduction electrons (not valence electrons or ions), no crystal structure or chemical detail (except valence), and focuses on averages (velocity, scattering time, density) rather than standard deviations, ...
In hindsight, it is all "obvious" and "reasonable" but spare a thought for Drude in 1900. It was only 3 years after the discovery of the electron, before people were even certain that atoms existed, and certainly before the Bohr model...
This issue is worth thinking about as we struggle to describe and understand complex systems such as society, the economy, or biological networks. One can nicely see 1. and 2. above in a modest and helpful article by William Bialek, Perspectives on theory at the interface of physics and biology.
Subscribe to:
Posts (Atom)
What Americans might want to know about getting a job in an Australian university
Universities and scientific research in the USA are facing a dire future. Understandably, some scientists are considering leaving the USA. I...
-
Is it something to do with breakdown of the Born-Oppenheimer approximation? In molecular spectroscopy you occasionally hear this term thro...
-
Nitrogen fluoride (NF) seems like a very simple molecule and you would think it would very well understood, particularly as it is small enou...
-
I welcome discussion on this point. I don't think it is as sensitive or as important a topic as the author order on papers. With rega...