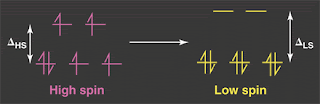Single orbital + multiple sites = Rich physics

Since the discovery of the iron-based superconductors, it has become clear that the combination of multiple orbitals and strong correlations can lead to rich physics, beyond what one sees in single orbital routes.
An alternative route to rich physics is a single orbital model on a lattice with multiple sites in a unit cell.

Henry Nourse, Ben Powell, and I just posted a preprint
Multiple insulating phases due to the interplay of strong correlations and lattice geometry in a single-orbital Hubbard model

We find ten distinct ground states for the single-orbital Hubbard model on the decorated honeycomb lattice, which interpolates between the honeycomb and kagome lattices and is the simplest two-dimensional net. The rich phase diagram includes a real-space Mott insulator, dimer, and trimer Mott insulators, a spin-triplet Mott insulator, flat band ferromagnets, and Dirac metals. It is determined as a function of interaction strength, band filling, and hopping anisotropy, using rotationally invariant slave boson mean-field theory.

We welcome comments.

Orbital-selective bad metals

Alejandro Mezio and I just posted a preprint
Orbital-selective bad metals due to Hund’s rule and orbital anisotropy: a finite-temperature slave-spin treatment of the two-band Hubbard model

The central result is shown in the Figure below. It shows the phase diagram of the metallic phase as a function of temperature and the Hund's rule interaction J in a system with two bands of differing bandwidth. Uc1 ~ W1 is the critical interaction for a Mott insulator in a one band system with bandwidth W1.
The system is a Hund's metal in that the strong correlations arise from J and not from proximity to a Mott insulating phase (note that U=0.5Uc1).
In the orbital-selective bad metal, one of the bands is a coherent Fermi liquid (with well-defined Fermi surface) and the second (narrower) band is a bad metal.

Two things that I find particularly interesting are the following.

Stability of the bad metal and the orbital-selective bad metal are enhanced by increasing J and/or by increasing band anisotropy.

The temperatures at which the bad metals occur is orders of magnitude smaller than the Fermi temperature for the corresponding non-interacting system (being of the order of W1~ Uc1).

We welcome comments.

Imaging orbital-selective quasi-particles in a Hund's metal

Over the past two decades, a powerful new technique has been developed to determine quasi-particle properties in strongly correlated electron systems, based on STM (scanning tunneling microscope) measurements. Quasi-particle interference (QPI) has proved to be particularly useful for studying cuprates (e.g. in revealing the d-wave pairing) and now for iron-based superconductors. The basic physics is as follows. One measures the changes in the local tunneling density of states N(r,E), associated with a single impurity that scatters quasi-particles with a change in momentum q. Then the Fourier transform of this change is

The text above is taken from a nice paper
Imaging orbital-selective quasiparticles in the Hund’s metal state of FeSe 
A. Kostin, P.O. Sprau, A. Kreisel, Yi Xue Chong, A.E. Böhmer, P.C. Canfield, P.J. Hirschfeld, B.M. Andersen and J.C. Séamus Davis

They show theoretically that the intensity of the interference pattern is quite sensitive to the quasi-particle weights of the different d-orbital bands. The experiments are consistent with

The key figure is below. It shows shaded intensity plots of the change in DOS as a function of wavevector. The central column is experimental data with E increasing from -20 meV to +15 meV as one goes down the column. The left and right columns show theoretical values for the same quantities, calculated with all the quasi-particle weights Z=1 (left) and the Z values above (right).   

   

The large variation between the Z values for different orbitals shows how the effect of the correlations are orbital selective.

The same Z values were used by the same cast of characters in a study of the superconducting state that showed orbital selectivity played a key role in the Cooper pairing, including the significant variation of the energy gaps over the different Fermi surfaces. The quantitative agreement between experiment and the associated theory is quite impressive.

I thank Alejandro Mezio for bringing the papers to my attention.

Superconductivity in a Hund's metal

The BCS theory of superconductivity is one of the towering intellectual achievements of the twentieth century. There are many ingredients to the theory and many significant results. One key step is to consider an effective interaction that is responsible for the Cooper pairing. A key result is that many properties are universal in that one can rescale temperatures and energies by the energy gap (at zero temperature), Delta(0) or the transition temperature Tc. In the limit of weak-coupling there is a universal ratio
2 Delta(0)/kTc = 3.5
Most elemental superconductors are consistent with this value. Some such as Hg and Pb have larger values, but these can actually be calculated when strong coupling effects are taken into account, via the Eliashberg equations.

Unconventional superconductors (cuprate, organic, heavy fermion, iron based) have resisted a simple unifying theory and universal trends, comparable to the stellar success of BCS theory. For example, the gap/Tc ratio is all over the place. However, there has been some progress for the iron-based superconductors. Recent ARPES results (summarised in the figure at the bottom below) have shown a universal ratio, of about 7.2 for a wide range of materials.

A fascinating feature of these iron-based materials is the nature of the metallic state that undergoes the superconducting instability. I have written several blog posts about the Hund's metal. One important feature is that there is relatively low coherence temperature below which a Fermi liquid metal forms, and there is a correspondingly low energy scale Omega0 associated with spin fluctuations, which become very slow. This arises from the rich Kondo physics associated with the multi-orbital character of the system. Furthermore, the spin fluctuation spectrum has a power law dependence above Omega0.

The above ideas come together in an interesting preprint
On the Superconductivity of Hund's Metals 
Tsung-Han Lee, Andrey Chubukov, Hu Miao, Gabriel Kotliar

They consider a single band superconductor described by the strong-coupling Eliashberg equations where the frequency dependence of the (effective) electron-electron attraction is given by

where the exponent gamma is treated as a variable. The Eliashberg equations are solved (for a single band) and give the following relationship between the gap ratio and the exponent gamma.

The value of gamma=1.2 is that associated with the relevant Kondo problem above the coherence temperature. The gap ratio corresponds to the black dashed line in the graph below.

One thing should be stressed here is that one is observing a transition from an incoherent metal into a superconductor, unlike in the BCS situation where the transition is from a coherent Fermi liquid.
I thank Alejandro Mezio for bringing the paper to my attention.

Emergent temperature scales and spin-orbital separation in the Hund's metal

An important and fascinating issue in many-body physics is the emergence of new energy scales, particularly scales that are orders of magnitude smaller than the energy scales in the underlying Hamiltonian. One example is the coherence temperature associated with the crossover from a Fermi liquid (with coherent quasi-particles) to a bad metal.

Recently, I posted about the crossover from a Hund's metal to a bad metal, seen in the collapse of the Drude peak in the optical conductivity, and the issue of capturing this slave-particle theories. One commenter mentioned the relevance of the paper below and another asked about the claim that the Kondo effect is associated with the collapse.

I agree that Kondo physics is associated with the crossover. Although, far from obvious this is also the case in the single-band Hubbard model. The Kondo effect was first studied with isolated magnetic impurities in metals and can be described by a single-impurity Anderson model (SIAM). Although there are no magnetic impurities in the Hubbard model, it turns out that when studied at the level of Dynamical-Mean-Field Theory (DMFT), the model is described by a self-consistent SIAM and close to the Mott metal-insulator transition Kondo physics does emerge. Specifically, the Kondo temperature for the self-consistent SIAM corresponds to the temperature at which there is a crossover from local unscreened local magnetic moments (associated with the almost-localised electrons near the Mott phase; the bad metal) to a Fermi liquid where the "magnetic moments" are screened.

What happens in a two-band Hubbard-Kanamori model with Hund's rule coupling?

The physics is richer because there is now the possibility screening of spin and/or orbital degrees of freedom, and of a orbital-selective Mott phase (or bad metal). 

This is nicely investigated in the following paper.

Dynamical Mean-Field Theory Plus Numerical Renormalization-Group Study of Spin-Orbital Separation in a Three-Band Hund Metal
K. M. Stadler, Z. P. Yin, J. von Delft, G. Kotliar, and A. Weichselbaum

For me, the figure below is the most interesting and illuminating. It shows how due to the Hund's rule coupling, two distinct energy scales (differing by about two orders of magnitude) emerge and associated with screening the spin and orbital degrees of freedom, respectively.

This is Kondo physics, but there are no magnetic impurties.

Experimental observation of the Hund's metal to bad metal crossover

A definitive experimental signature of the crossover from a Fermi liquid metal to a bad metal is the disappearance of a Drude peak in the optical conductivity. In single band systems this occurs in proximity to a Mott insulator and is particularly clearly seen in organic charge transfer salts and is nicely captured by Dynamical Mean-Field Theory (DMFT).

An important question concerning multi-band systems with Hund's rule coupling, such as iron-based superconductors, is whether there is a similar collapse of the Drude peak. This is clearly seen in one material in a recent paper

Observation of an emergent coherent state in the iron-based superconductor KFe2As2 
Run Yang, Zhiping Yin, Yilin Wang, Yaomin Dai, Hu Miao, Bing Xu, Xianggang Qiu, and Christopher C. Homes

Note how as the temperature increases from 15 K to 200 K that the Drude peak collapses. 

The authors give a detailed analysis of the shifts in spectral weight with varying temperature by fitting the optical conductivity (and reflectivity from which it is derived) at each temperature to a model consisting of three Drude peaks and two Lorentzian peaks. Note this involves twelve parameters and so one should always worry about the elephants trunk wiggling.

On the other hand, they do the fit without the third peak, which is of the greatest interest as it is the sharpest and most temperature dependent, and claim it cannot describe the data.

The authors also perform DFT+DMFT calculations of the one-electron spectral function (but not the optical conductivity) and find it does give a coherent-incoherent crossover consistent with the experiment. However, the variation in quasi-particle weight with temperature is relatively small.

Questions about slave-particle mean-field theories of Hund's metals

One of most interesting new ideas about quantum matter from the last decade is that of a Hund's metal. This is a strongly correlated metal that can occurs in a multi-orbital material (model) as a result of the Hund's rule (exchange interaction) J that favours parallel spins in different orbitals.
Above some relatively low temperature (i.e. compared to the bare energy scales such as non-interacting band-widths, J, and Hubbard U) the metal becomes a bad metal, associated with incoherent excitations.
An important question concerns the extent to which slave mean-field theories can capture the stability of the Hund's metal, and its properties including the emergence of a bad metal above some coherence temperature, T*.

In a single-band Hubbard model, the strongly correlated metallic phase that occurs in proximity to a Mott insulator is associated with a small quasi-particle weight and suppression of double occupancy, reflecting suppressed charge fluctuations. This is captured by slave-boson mean-field theory, including the small coherence temperature.

In contrast, to a "Mott metal", a Hund's metal is associated with suppression of singlet spin fluctuations on different orbitals, without suppression of charge fluctuations and is seen in a Z_2 slave-spin mean-field theory at zero temperature.

Specific questions are whether slave mean-field theories at finite temperature can capture the following?

• The coherence temperature, T*.
• A suppression of spin singlet fluctuations at T increases towards T*.
• An orbital-selective bad metal may occur in proximity to an orbital selective Mott transition. This is where at least one band (orbital) is a Fermi liquid and another is a bad metal. This would mean that there are two different coherence temperatures. 
• The emergence of a single low-energy scale, common in both bands, as is seen in DMFT.
• The spin-freezing temperature.

Finally, how does the stability of the Hund's metal change with the number of orbitals?
Figures in this post suggest that the Hund's physics is more pronounced with increasing the number of orbitals. However, that may be because the critical U (and thus proximity to the Mott insulator) changes with the number of orbitals and all the curves are for the same U.

What do you call a mixture of a bad metal and a good metal?

It is fun to come up with clever names for new physical phenomena: quark, big bang, Janus, slepton,  chromodynamics, inflation, squashon, ...
There is an amusing article by David Mermin about how he managed to get boojum  accepted as a scientific term.
Can you think of others?

What is a good synonym for something that has both good and bad qualities?
A curate's egg?

I was wondering about this because of thinking about a metal that is a mixture of a good metal and a bad metal. This is relevant close to an orbital-selective Mott transition. There it may be possible to have multiple Fermi liquids (associated with multiple bands) at low temperatures with different coherence temperatures. For example, this does occur in strontium ruthenate.  As a result, when the temperature is increased one can enter a state in which one of the bands has coherent quasi-particles (and a well-defined Fermi surface) and another does not, i.e. it is a bad metal.

A relevant paper is
Observation of Temperature-Induced Crossover to an Orbital-Selective Mott Phase in AxFe2-ySe2 (A 1⁄4 K, Rb) Superconductors 
M. Yi, D. H. Lu, R. Yu, S. C. Riggs, J.-H. Chu, B. Lv, Z. K. Liu, M. Lu, Y.-T. Cui, M. Hashimoto, S.-K. Mo, Z. Hussain, C. W. Chu, I. R. Fisher, Q. Si, and Z.-X. Shen

They present ARPES data, including that below, that shows how the spectral intensity changes as the temperature increases. The blue and red curves are identified with different d-orbital bands.

Being cautious, I am a bit wary about how clearly the data do support the conclusions. Nevertheless, ...
The authors also present a slave-spin theory calculation for a five-band Hubbard-Kanamori model that is consistent with the experimental data.

I thank Alejandro Mezio for helpful discussions about this topic.

Low energy scales near the orbital-selective Mott transition

One of the most fundamental and profound concepts in quantum many-body theory is the emergence of low energy scales that are much smaller than the energy scales in the "bare" Hamiltonian.
For example, in a metallic phase near the Mott transition in a single band system, there is the energy scale associated with a Fermi liquid. Studies using Dynamical Mean-Field Theory (DMFT) have shown how this scale is associated with ``kinks'' in the quasi-particle dispersion relation and is related to the energy scale for spin fluctuations.

The problem of the Mott transition in multi-band systems (degenerate orbitals) is fascinating and of renewed interest since the discovery of iron-based superconductors. A basic question concerns how the Mott transition is qualitatively different from in single band systems. More specifically, how does a Hund's rule coupling change things?

One new concept is that of an orbital-selective Mott transition. This is where one or more of the bands remains metallic but others become Mott insulators. This concept was originally introduced to explain the intriguing properties of Ca_xSr_2-xRuO4 with x ~ 0.5: it is metallic but has localised spin-1/2 magnetic moments.
[For a critical discussion see the  nice review Strong correlations from Hund's coupling by Antoine Georges, Luca de' Medici, and Jernej Mravlje.]

One might expect that near this transition there are separate low energy scales associated with each of the bands and that these scales are quite different for the bands that become insulator.
However, this is not the case.

There is a nice paper
Emergence of a Common Energy Scale Close to the Orbital-Selective Mott Transition 
Markus Greger, Marcus Kollar, and Dieter Vollhardt

They use DMFT to study a two-band Hubbard model with different bandwidths. They calculate the one-electron spectral functions, the electronic self energy, and the dynamical spin susceptibilities.

The left panel below shows the spectral functions for the two bands. Note how for one the quasi-particle peak width is much smaller than the other.
The right panel (top) shows the energy dependence of the real part of the self-energy for the two bands. Surprisingly, the kink occurs at the same energy.
Furthermore, the bottom of the right panel shows that this peak corresponds to the peak in the dynamical spin susceptibility for both bands.

The figure below shows that "If the Hund’s rule coupling is sufficiently strong, one common energy scale emerges which characterizes both the location of kinks in the self-energy and extrema of the diagonal spin susceptibilities."

The authors then give a physical explanation of this energy scale from a two-impurity Kondo model.

A molecular material and a model Hamiltonian with rich physics

Some of my UQ colleagues and Jaime Merino have written a series of nice papers inspired by an organometallic molecular material Mo3S7(dmit)3. They have considered possible model effective Hamiltonians to describe it and the different ground states that arise depending on the model parameters.
There is a rich interplay of strong correlations, Hund's rule coupling, spin frustration, spin-orbit coupling, flat bands, and Dirac cone physics.
Possible ground states include some sort of Mott insulator, a Haldane phase, semi-metal, ...

A good place to start is the following paper
Low-energy effective theories of the two-thirds filled Hubbard model on the triangular necklace lattice 
C. Janani, J. Merino, Ian P. McCulloch, and B. J. Powell

The figure below (taken from this paper) shows some of the molecular structure and some of the hopping integrals that are associated with an underlying decorated honeycomb lattice.

This model could be called kagomene, because it interpolates between the kagome lattice and the honeycomb lattice (graphene). The figure below is taken from this paper, which uses DFT and Wannier orbitals to estimate the tight-binding parameters and the spin-orbit coupling. Interaction driven topological insulator states are possible on this lattice.

There are a few things that are not "normal" about the physics, arising from the 4/3 band filling and the molecular orbitals that are delocalised over the triangles. Specifically, the orbital degeneracy does not arise from atomic orbital degeneracy (cf. d orbitals, or t2g and eg), but rather the E representation associated with C3 symmetry of the triangles.

Hund's rule coupling. 
This involves the E orbitals and arises purely from the Hubbard U on the non-degenerate orbital on a single lattice site.

Spin-orbital coupling.
This is Spin Molecular Orbital Coupling, where the electron spin couples to the angular momentum associated with motion around the triangle, not the angular momentum of degenerate atomic orbitals.

Haldane phase.
The associated spin-1's arise from the triplet ground state of four electrons on a triangle.
A DMRG study shows that this is the ground state of a three leg-ladder Hubbard model at 2/3 filling.

Many interesting and important open questions remain about the general phase diagram of the Hubbard model on the kagomene lattice. For example, the nature of the Mott insulator, different types of topological order, the possibility of superconductivity.....

Hopefully, these studies will stimulate new experimental studies and synthesis of new chemical compounds in this fascinating class of materials.

A new picture of unconventional superconductivity

Two key ideas concerning unconventional superconductors are the following.

1. s-wave and p-wave pairing (in momentum space) are associated with spin singlet and spin triplet pairing, respectively. This can be shown with minimal assumptions (no spin-orbit coupling and spatial inversion symmetry).

2. If superconductivity is seen in proximity to an ordered phase (e.g. ferromagnetism or antiferromagnetism) with a quantum critical point (QCP) then the pairing can be "mediated" by low energy fluctuations (e.g. magnons) associated with the ordering.

3. Non-fermi liquid behaviour may be seen in the quantum critical region about the QCP.

However, an interesting paper shows that neither of the above is necessarily true.

Superconductivity from Emerging Magnetic Moments 
Shintaro Hoshino and Philipp Werner

They find spin triplet superconductivity with s-wave symmetry. This arises because there is more than one orbital per site and due to the Hund's rule coupling spin triplets can form on a single site.

They also find the pairing is strongest near the "spin freezing crossover" which is associated with the "Hund's metal", i.e. the bad metal arising from the Hund's rule interaction, and has certain "non-Fermi liquid" properties.

The results are summarised in the phase diagrams below, which has a striking similarity to various experimental phase diagrams that are usually interpreted in terms of 2. above.
However, all the theory is DMFT and so there are no long wavelength fluctuations.

The many scales of emergence in the Haldane spin chain

The spin-1 antiferromagnetic Heisenberg chain provides a nice example of emergence in a quantum many-body system. Specifically, there are three distinct phenomena that emerge that were difficult to anticipate: the energy gap conjectured by Haldane, topological order, and the edge excitations with spin-1/2.

An interesting question is whether anyone could have ever predicted these from just knowing the atomic and crystal structure of a specific material. I suspect Laughlin and Pines would say no.

To understand the emergent properties one needs to derive effective Hamiltonians at several different length and energy scales. I have tried to capture this in the diagram below. In the vertical direction, the length scales get longer and the energy scales get smaller.

It is interesting that one can get the Haldane gap from the non-linear sigma model. However, it coarse grains too much and won't give the topological order or the edge excitations.

It seems to me that the profundity of the emergence that occurs at the different strata (length scales) is different. At the lower levels, the emergence is perhaps more "straightforward" and less surprising or less singular (in the sense of Berry).

Aside. I spend too much time making this figure in PowerPoint. Any suggestions on a quick and easy way to make such figures?

Any comments on the diagram would be appreciated.

Bad metals, Mott insulators, and superconductivity in fullerenes

Last week in Ljubljana, I had a nice discussion with Denis Arčon about this paper concerning fullerenes, A3C60 where A = alkali metal.

Optimized unconventional superconductivity in a molecular Jahn-Teller metal
Ruth H. Zadik, Yasuhiro Takabayashi, Gyöngyi Klupp, Ross H. Colman, Alexey Y. Ganin, Anton Potočnik, Peter Jeglič, Denis Arčon, Péter Matus, Katalin Kamarás, Yuichi Kasahara, Yoshihiro Iwasa, Andrew N. Fitch, Yasuo Ohishi, Gaston Garbarino, Kenichi Kato, Matthew J. Rosseinsky and Kosmas Prassides

This is a rich system and is summarised in the (temperature vs. volume) phase diagram below. Superconductivity appears in proximity to a Mott (Jahn-Teller) insulator.

The JT metal is a bad metal. The novel signature here is that because the electrons are almost localised on individual molecules there is Jahn-Teller effect. This is seen in the Fano line shape of the associated vibrational spectra.

Aside: I have often wondered about a good theoretical description of the Fano line shape for vibrational spectra in metals because it is quite common in organic charge transfer salts. There is an old theory by Michael Rice.  However, it does not even mention Fano. 

Yesterday, Darko Tanaskovic brought to my attention a nice paper which explicitly relates the Rice theory, the relevant Feynman diagrams, to the Fano form for the spectral density. (See especially, Section III).

Charged-phonon theory and Fano effect in the optical spectroscopy of bilayer graphene 
 E. Cappelluti, L. Benfatto, M. Manzardo, and A. B. Kuzmenko

For these fullerenes the minimal effective Hamiltonian is a three band Hubbard model with Hund's rule coupling and electron-phonon interaction (which leads to the Jahn-Teller effect on isolated C60 molecules. Extensive calculations based on Dynamical Mean-Field Theory (DMFT) describe this phase diagram and have been reviewed by Massimo Capone, Michele Fabrizio, Claudio Castellani, and Erio Tosatti

Strong correlations and thermal expansion in iron based superconductors

There is a nice preprint
Strong Correlations, Strong Coupling and s-wave Superconductivity in Hole-doped BaFe2As2 Single Crystals 
F. Hardy, A. E. Böhmer, L. de' Medici, M. Capone, G. Giovannetti, R. Eder, L. Wang, M. He, T. Wolf, P. Schweiss, R. Heid, A. Herbig, P. Adelmann, R. A. Fisher, C. Meingast

The figures below summarise some of the key physics. The top is the phase diagram.

The bottom shows the specific heat coefficient gamma as a function of alkali metal content (Cs to Rb to K, and then fractional K content (doping x).

Note that

a. The black curve shows values calculated from density functional theory (DFT) based calculations. The blue points are experimental data, which are as much as an order of magnitude larger, reflecting strong correlations.

b. As one goes K to Rb to Cs the correlations are enhanced, somehow reflecting the "negative pressure" associated with the increasing ion size.

c. The experimental trend is captured nicely by calculations using slave spins (SS) to treat the relevant multi-band Hubbard model with Hund's rule coupling and band structure from DFT.

The thermal expansion alpha is particularly interesting because it is dominated by electronic effects (unlike in most metals) and shows a coherent-incoherent crossover from a Fermi liquid (where alpha/T is constant) to a bad metal at a temperature T*.
As one goes K to Rb to Cs alpha/T is enhanced reflecting the increased correlations.

One reason I am particularly interested in the manifestation of strong correlations in the thermal expansion because this also occurs in organic charge transfer salts, as discussed at length in a recent paper I published with Jure Kokalj. But, we did struggle to obtain a detailed quantitative description of the experiments, partly because of the crystallographic complexity.
It would be nice to see if a DMFT + LDA treatment of the relevant model for these iron compounds could describe the data above.

I thank Christoph Meingast for bringing this work to my attention and helpful discussions about it.

The key physics of spin crossover compounds

In Telluride Francesco Paesani gave a nice talk about his work on metal-organic-frameworks, including those that exhibit spin crossover.

The underlying physics is fascinating as there is a subtle interplay of electronic, magnetic, and lattice effects. The crossover/transition is actually driven by changes in the vibrational entropy.

Spin "crossovers" involve a transition such as that shown above, from a S=2 state (HS=high spin) to a S=0 state (LS=low spin) often seen in Fe(2+) compounds.This transition occurs as the temperature is decreased, and sometimes is not a crossover, but a first order transition with hysteresis.

Spin crossover in metal-organic frameworks (MOFs) are of such great interest because the transition temperature can

•  be comparable to room temperature
• vary significantly as the MOF (which is very porous) adsorbs "guest" molecules such as water.

These properties have significant technological potential but also involve some fascinating science I want to elucidate here.

First, what determines the transition temperature?
In a simple two state model it is given by the ratio of the energy (enthalpy) difference between the two states and the  entropy difference between them,

The energy difference between LS and HS = 2U - 2J -2 Delta where
U = Hubbard interaction = Coulomb interaction in a single d orbital
J = Hund's rule interaction favouring parallel spin in degenerate orbitals
Delta = Crystal field splitting of d-orbitals (e.g. the t_2g - e_g splitting in an octahedral environment).

Typically, we would expect this energy difference to be a substantial fraction of an eV (i.e. thousand's of Kelvin), unless there is some amazing cancellation (fine tuning) going on. Indeed, as shown below our expectations our correct.

Also, given one is looking at the difference between large energies one should be cautious about getting accurate values of this quantity from quantum chemical methods.

A first guess for the entropy difference between the high and low spin states is the difference in spin entropy, k_B ln (5). This explains why the HS state occurs at high temperatures. However, taking this guess with that for the energy difference gives a transition temperature of thousands of Kelvin. So the entropy difference must be much larger and due to something else.

Theoretical Modeling of Spin Crossover in Metal–Organic Frameworks: [Fe(pz)2Pt(CN)4] as a Case Study 
 Jordi Cirera, Volodymyr Babin, and Francesco Paesani

The figure below shows the calculated energy of the HS and LS state versus delta = average value of the six metal-ligand bonds.

Three key observations are

• the energy gap between the two states is about 10 kcal/mol (0.4 eV corresponding to a temperature of about 5000 K).
• the low spin-high spin transition is associated with a significant lattice distortion of about 0.2 Angstroms.
• the high spin state is much "softer" (the parabola has a smaller curvature), i.e, the metal-ligand stretch frequency will be significantly smaller

The solid and dashed curves correspond to two different computational approaches. The latter is based on density functional theory (DFT). The former is empirical, ligand field force field (LF-FF), a method I previously  highlighted of value  for modelling transition metal complexes in proteins.

I also note that the crystal field splitting (ligand field for chemists) Delta = 10,000 cm^-1 and
so  2 Delta = 2.5 eV and the HS-LS energy difference does involve subtle differences.

The harmonic vibrational frequencies for modes less than 500 cm-1 (comparable to room temperature) are calculated and it is found that these thirty modes are softer in the HS state, leading to a higher entropy in the HS state. Using the associated entropy difference gives a value of the transition temperature that is comparable to experiment.

It is argued that these modes are softer because in the HS state the anti-bonding e_g orbitals are occupied and so the bonds are softer. I understand this argument for modes such as the metal-ligand modes. However, it is not clear to me why this matters for (the many) modes such as those largely localised on the ligands.

Thus, there is a theoretical understanding of the first outstanding property of spin crossover in MOFs: the relatively low transition temperature.
What about the second property: the dependence on adsorbed molecules?

Molecular Mechanisms of Spin Crossover in the {Fe(pz)[Pt(CN)4]} Metal–Organic Framework upon Water Adsorption 
 C. Huy Pham, Jordi Cirera, and Francesco Paesani

The decrease of the spin-crossover temperature of {Fe(pz)[Pt(CN)4]} upon water adsorption predicted by the simulations is in agreement with the available experimental data and is traced back to the elongation of the bonds between the Fe(II) atoms and the organic linkers induced by interactions of the adsorbed water molecules with the framework.

Again the key is the change in vibrational entropy. Upon adsorption the modes get softer.

There is more direct experimental evidence for
Role of Molecular Vibrations in the Spin Crossover Phenomenon
Jean-Pierre Tuchagues , Azzedine Bousseksou, Gábor Molnár, John J. McGarvey, François Varret

That review considers how IR, Raman, and specific heat measurements show softening of a wide range of vibrations in the HS state.

To me outstanding theoretical issues concern

• how the HS state softens so many vibrational modes
• defining a simple model effective Hamiltonian that captures the interplay of spin and the vibrational degrees of freedom
• describing and understanding co-operative effects that lead to the first order transition and hysteresis. 

Lineage of the Janus god metaphor in condensed matter

Five years ago, Antoine Georges and collaborators invoked the metaphor of the greek god Janus to represent the "two-faced" effects of Hund's coupling in strongly correlated metals.

I wondered where they got this idea from: was it from someones rich classical education?
In the KITP talk, I recently watched online, Antoine mentioned he got the idea from Pierre de Gennes.

In his 1991 Nobel Lecture, de Gennes said

the Janus grains, first made by C. Casagrande and M. Veyssie. The god Janus had two faces. The grains have two sides: one apolar and the other polar. Thus they have certain features in common with surfactants. But there is an interesting difference if we consider the films which they make —for instance, at a water-air interface. A dense film of a conventional surfactant is quite impermeable. On the other hand, a dense film of Janus grains always has some interstices between the grains, and allows for chemical exchange between the two sides: "the skin can breathe. " This may possibly be of some practical interest.

Here are some images of "Janus particles".

KITP seminars online

A wonderful thing about the web is that now there is so much material online. A pioneer in putting all their seminars and colloquia online is the KITP at Santa Barbara. I know some people who regularly watch seminars (both old and recent). Others do not know it exist. This is a particularly valuable resource for students and those of us in distant countries.

I have to confess that until yesterday I have never actually watched a talk; just occasionally skimmed some slides. Generally I find I don't have the patience to watch talks online. I just seem to prefer to look at papers. However, yesterday I was forced to do this because at the weekly UQ condensed matter theory group meeting we watched a nice talk by Antoine Georges on Hund's metals. Although, I have read and blogged about some of the relevant papers, I really found it helpful seeing what was highlighted and going through the material at a "slow pace". Hopefully, I will do this more often.

What do you think about online talks or lectures? How often do you watch them? Are there any that you would particularly recommend?

The essence of the Hund's metal

I think one of the most interesting ideas to emerge in the theory of correlated electron materials over the past five years is that of a Hund's metal, particularly how bad metal behaviour is enhanced by the presence of the Hund's rule coupling associated with degenerate d-orbitals and multiple bands.  This is relevant to many transition metal compounds. I recently found the following paper quite helpful. It builds on important earlier work by Luca de Medici.

Electronic correlations in Hund metals
L. Fanfarillo and E. Bascones

A couple of key ideas.

In a single band Hubbard model as one approaches the Mott insulator the probability of double occupancy decreases and so does the local charge fluctuations. This reduces the quasi-particle weight Z, which is the overlap of the ground state with a non-interacting Fermi sea.
A Hund's metal is different.

Hund's coupling polarizes the spin locally. The small Z in a Hund metal is due to the small overlap between the noninteracting states and the spin polarized atomic states [5,7,36]. The suppression of Z is thus concomitant with an enhancement of the spin fluctuations CS; see Fig. 3(a) [below].

Here CS=⟨S2⟩−〈S〉2 with 〈S〉=0 and S=12∑a=1,...,N(na↑−na↓). Arrows in Fig. 3(a) mark J∗H(U) the interaction at which the system enters into the Hund metal defined empirically as the value of JH with the strongest suppression of Z, i.e., the most negative dZ/dJH value, after which Z stays finite; see Fig. S2(c) in SM [35]. Above J∗H, CS reaches a value close to that of the Mott insulator at this filling showing that in the Hund metal state each atom is highly spin polarized, Figs. 3(a) and S3(b) and S3(c) in SM [35].

The three curves (black, green, red) correspond to 5 electrons in 6 orbitals, 3 electrons in 4 orbitals, and 2 electrons in 3 orbitals, respectively.

Unlike in a single band, as the system becomes more correlated (with increasing Hund's coupling J_H) the charge fluctuations can increase, as shown below.

It would be interesting to see how much of this essential physics is captured in a two-site Hubbard-Kanomori model such as this one.

An important open question is whether the signatures of a bad metal (such as thermopower of order k_B/e, no Drude peak, .... are the same for a Hund's metal and a single band system.