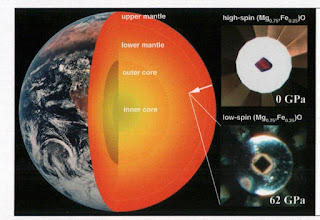
Superconductivity: a poster child for emergence

Superconductivity beautifully illustrates the characteristics of emergent properties.

Novelty. 

Distinct properties of the superconducting state include zero resistivity, the Meissner effect, and the Josephson effect. The normal metallic state does not exhibit these properties.

At low temperatures, solid tin exhibits the property of superconductivity. However, a single atom of tin is not a superconductor. A small number of tin atoms has an energy gap due to pairing interactions, but not bulk superconductivity.

There is more than one superconducting state of matter. The order parameter may have the same symmetry as a non-trivial representation of the crystal symmetry and it can have spin singlet or triplet symmetry. Type II superconductors in a magnetic field have an Abrikosov vortex lattice, another distinct state of matter.

Unpredictability. 

Even though the underlying laws describing the interactions between electrons in a crystal have been known for one hundred years, the discovery of superconductivity in many specific materials was not predicted. Even after the BCS theory was worked out in 1957 the discovery of superconductivity in intermetallic compounds, cuprates, organic charge transfer salts, fullerenes, and heavy fermion compounds was not predicted.71

Order and structure. 

In the superconducting state, the electrons become ordered in a particular way. The motion of the electrons relative to one another is not independent but correlated. Long-range order is reflected in the generalised rigidity, which is responsible for the zero resistivity. Properties of individual atoms (e.g., NMR chemical shifts) are different in vacuum, metallic state, and superconducting state.

Universality. 

Properties of superconductivity such as zero electrical resistance, the expulsion of magnetic fields, quantisation of magnetic flux, and the Josephson effects are universal. The existence and description of these properties are independent of the chemical and structural details of the material in which the superconductivity is observed. This is why the Ginzburg-Landau theory works so well. In BCS theory, the temperature dependences of thermodynamic and transport properties are given by universal functions of T/Tc where Tc is the transition temperature. Experimental data is consistent with this for a wide range of superconducting materials, particularly elemental metals for which the electron-phonon coupling is weak.

Modularity at the mesoscale. 

Emergent entities include Cooper pairs and vortices. There are two associated emergent length scales, typically much larger than the microscopic scales defined by the interatomic spacing or the Fermi wavelength of electrons. The coherence length is associated with the energy cost of spatial variations in the order parameter. It defines the extent of the proximity effect where the surface of a non-superconducting metal can become superconducting when it is in electrical contact with a superconductor. The coherence length turns out to be of the order of the size of Cooper pairs in BCS theory.  The second length scale is the magnetic penetration depth (also known as the London length) which determines the extent that an external magnetic field can penetrate the surface of a superconductor. It is determined by the superfluid density. The relative size of the coherence length and the penetration depth determines whether  the formation of an Abrikosov vortex lattice is stable in a large enough magnetic field.

Quasiparticles. 

The elementary excitations are Bogoliubov quasiparticles that are qualitatively different to particle and hole excitations in a normal metal. They are a coherent superposition of a particle and hole excitation (relative to the Fermi sea), have zero charge and only exist above the energy gap. The mixed particle-hole character of the quasiparticles is reflected in the phenomenom of Andreev reflection.

Singularities. 

Superconductivity is a non-perturbative phenomenon. In BCS theory the transition temperature, Tc, and the excitation energy gap are a non-analytic function of the electron-phonon coupling constant lambda, Tc \sim exp(-1/lambda).

A singular structure is also evident in the properties of the current-current correlation function. Interchange of the limits of zero wavevector and zero frequency do not commute, this being intimately connected with the non-zero superfluid density.

Effective theories.

These are illustrated in the Figure below. The many-particle Schrodinger equation describes electrons and atomic nuclei interacting with one another. Many-body theory can be used to justify considering the electrons as a jellium liquid of non-interacting fermions interacting with phonons. Bardeen, Pines, and Frohlich showed that for that system there is an effective interaction between fermions that is attractive. The BCS theory includes a truncated version of this attractive interaction. Gorkov showed that Ginzburg-Landau theory could be derived from BCS theory. The London equations can be derived from Ginzburg-Landau theory. The Josephson equations only include the phase of order parameter to describe a pair of coupled superconductors.

The historical of the development of theories mostly went downwards. London preceded Ginzburg-Landau which preceded BCS theory. Today for specific materials where superconductivity is known to be due to electron-phonon coupling and the electron gas is weakly correlated one can now work upwards using computational methods such as Density Functional Theory (DFT) for Superconductors or the Eliashberg theory with input parameters calculated from DFT-based methods. However, in reality this has debatable success. The superconducting transition temperatures calculated typically vary with the approximations used in the DFT such as the choice of functional and basis set, and often differ from experimental results by the order of 50 percent. This illustrates how hard prediction is for emergent phenomena.

Potential and pitfalls of mean-field theory. 

Mean-field approximations and theories can provide a useful guide as what emergent properties are possible and as a starting point to map out properties such as phase diagrams. For some systems and properties, they work incredibly well and for others they fail spectacularly and are misleading. 

Ginzburg-Landau theory and BCS theory are both mean-field theories. For three-dimensional superconductors they work extremely well. However, in two dimensions as long-range order and breaking of a continuous symmetry cannot occur and the physics associated with the Berezinskii-Kosterlitz-Thouless transition occurs. Nevertheless, the Ginzburg-Landau theory provides the background to understand the justification for the XY model and the presence of vortices to proceed. Similarly, the BCS theory fails for strongly correlated electron systems, but a version of the BCS theory does give a surprisingly good description of the superconducting state.

Cross-fertilisation of fields. 

Concepts and methods developed for the theory of superconductivity bore fruit in other sub-fields of physics including nuclear physics, elementary particles, and astrophysics. Considering the matter fields (associated with the electrons) coupled to electromagnetic fields (a U(1) gauge theory) the matter fields can be integrated out to give a theory in which the photon has mass. This is a perspective on the Meissner effect in which the magnitude of an external magnetic field decays exponentially as it penetrates a superconductor. This idea of a massless gauge field acquiring a mass due to spontaneous symmetry breaking was central to steps towards the Standard Model made by Nambu and by Weinberg. 

Wading through AI hype about materials discovery

 Discovering new materials with functional properties is hard, very hard. We need all the tools we can from serendipity to high-performance computing to chemical intuition. 

At the end of last year, two back-to-back papers appeared in the luxury journal Nature.

Scaling deep learning for materials discovery

All the authors are at Google. They claim that they have discovered more than two million new materials with stable crystal structures using DFT-based methods and AI.

On Doug Natelson's blog there are several insightful comments on the paper about why to be skeptical about AI/DFT based "discovery".

Here are a few of the reasons my immediate response to this paper is one of skepticism.

It is published in Nature. Almost every "ground-breaking" paper I force myself to read is disappointing when you read the fine print.

It concerns a very "hot" topic that is full of hype in both the science and business communities.

It is a long way from discovering a stable crystal to finding that it has interesting and useful properties.

Calculating the correct relative stability of different crystal structures of complex materials can be incredibly difficult.

DFT-based methods fail spectacularly for the low-energy properties of quantum materials, such as cuprate superconductors. But, they do get the atomic structure and stability correct, which is the focus of this paper.

It is a big gap between discovering a material that has desirable technological properties to one that meets the demanding criteria for commercialisation.

The second paper combines AI-based predictions, similar to the paper above, with robots doing material synthesis and characterisation.

An autonomous laboratory for the accelerated synthesis of novel materials

[we] realized 41 novel compounds from a set of 58 targets including a variety of oxides and phosphates that were identified using large-scale ab initio phase-stability data from the Materials Project and Google DeepMind

These claims have already been undermined by a preprint from the chemistry departments at Princeton and UCL.

Challenges in high-throughput inorganic material prediction and autonomous synthesis

We discuss all 43 synthetic products and point out four common shortfalls in the analysis. These errors unfortunately lead to the conclusion that no new materials have been discovered in that work. We conclude that there are two important points of improvement that require future work from the community: 

(i) automated Rietveld analysis of powder x-ray diffraction data is not yet reliable. Future improvement of such, and the development of a reliable artificial intelligence-based tool for Rietveld fitting, would be very helpful, not only to autonomous materials discovery, but also the community in general.

(ii) We find that disorder in materials is often neglected in predictions. The predicted compounds investigated herein have all their elemental components located on distinct crystallographic positions, but in reality, elements can share crystallographic sites, resulting in higher symmetry space groups and - very often - known alloys or solid solutions. 

Life is messy. Chemistry is messy. DFT-based calculations are messy. AI is messy. 

Given most discoveries of interesting materials often involve serendipity or a lot of trial and error, it is worth trying to do what the authors of these papers are doing. However, the field will only advance in a meaningful way when it is not distracted and diluted by hype and authors, editors, and referees demand transparency about the limitations of their work.  

A Myth about Condensed Matter Physics?

What is condensed matter physics about? 

In his beautiful book, The Problems of Physics (originally published in 1987), Leggett has a nice chapter about condensed matter physics, Physics on a human scale. The abstract begins:

This chapter argues that the widespread notion that the discipline of condensed matter physics is devoted to deriving the properties of complex many-body systems from that of their atomic-level components is a myth, and that the analogy of map-making is much more appropriate.

Here are some quotes that clarify Leggett's argument.

a number of cases, particularly in the traditional areas of the physics of gases and crystalline solids, in which a model which treats the behaviour of the whole as essentially just the sum of that of its parts (atoms or electrons) has been quite successful; and a few more in which, even if a ‘one- particle’ picture fails, a description in terms of pairs of particles interacting in a way which is not particularly sensitive to the environment gives good results. But these cases, despite the fact that they totally dominate the presentation of the subject in most elementary textbooks, are actually the exception rather than the rule. 

In virtually all the frontier areas of modern condensed-matter physics, the relationship between our understanding of the behaviour of matter at the microscopic level of single atoms and electrons, and at the macroscopic level of (say) liquids and solids, is actually a good deal more complicated than this.

If the activity just described is not what condensed-matter physics is all about, then what is it about? I would claim that the most important advances in this area come about by the emergence of qualitatively new concepts at the intermediate or macroscopic levels—concepts which, one hopes, will be compatible with one's information about the microscopic constituents, but which are in no sense logically dependent on it. 

... [these new concepts] provide a new way of classifying a seemingly intractable mass of information, of selecting the important variables from the innumerable possible variables which one can identify in a macroscopic system;

All this is not to deny that an important role is played in condensed-matter physics by attempts to relate the macroscopic behaviour of bulk matter to our knowledge concerning its constituent atoms and electrons. Indeed, the theoretical literature on the subject is full of papers which at first sight seem to be claiming to ‘derive’ the former from the latter—that is, to do exactly what I have just said condensed-matter physicists do not do. 

It is precisely this compelling need to isolate, from a vast and initially undifferentiated mass of information, the features which are relevant to the questions one wishes to ask, which distinguishes condensed-matter physics qualitatively from areas such as atomic or particle physics...

In this situation I believe that it is sensible to reorient our view of the kinds of questions that we are really asking in condensed-matter physics. Rather than chasing after the almost certainly chimerical goal of deducing the behaviour of macroscopic bodies rigorously from postulates regarding the microscopic level, it may be better to view the main point of the discipline as, first, the building of autonomous concepts or models at various levels, ranging all the way from the level of atomic and subatomic physics to that of thermodynamics; and, second, the demonstration that the relation between these models at various levels is one not of deducibility but of consistency—that is, that there are indeed ‘physical approximations’ we can make which make the models at various levels mutually compatible.

In different words, condensed matter physics is all about emergence! [Although, I know Leggett does not like the way the word is used]. 

The centrality of intermediate scales was also emphasised by Tom McLeish in Soft Matter: A Very Short Introduction.

When I recently read Leggett's chapter I was concerned that this might be in conflict with my draft manuscript of Condensed Matter Physics: A Very Short Introduction.  In the first chapter, I wrote the following.

The central question of Condensed Matter Physics

Generally, condensed matter physicists grapple with one question. Because it is so important I state the question in three different ways.

• How do macroscopic properties emerge from microscopic properties? 

• How do the properties of a state of matter emerge from the properties of the atoms in the material and the interactions between the atoms?

• How do the many atoms in a material interact with one another to collectively produce a particular property of the material? 

I think this is consistent with Leggett's perspective, particularly because I do later emphasise emergence and intermediate scales. On the other hand, I may not have the same emphasis (or strong language) that Leggett does. 

Leggett's view is particularly pertinent today because a quarter of a century later there are probably a lot more people who would say that they are condensed matter physicists but would subscribe to the "myth". This is because of the rise of computational materials science due to massive increases in computational power and better computational methods such as those based on Density Functional Theory (DFT), using "better" functionals and DMFT (Dynamical Mean-Field Theory).

What do you think?

Mean-field theories: helpful or misleading? From Hubbard to COVID-19 models

Mean-field theory (self-consistent field theory) is incredibly valuable. It gives significant insights into what is possible with a particular model.
What kind of phases and broken symmetries may be possible?
How does the phase diagram depend on different parameters in a model?
Indeed, mean-field theory is the basis of the whole Landau paradigm for spontaneous symmetry breaking and phase transitions.
Implementations of Density Functional Theory (DFT) in computational materials science are basically mean-field theories. Most of computational quantum chemistry involves some sort of mean-field theory.

Mean-field theories do not take into account fluctuations, dynamic or spatial.
Basically, a many-body problem is reduced to a one-body problem.

A good mean-field theory can win you a Nobel Prize. That's what Anderson, BCS, Ginsberg, Abrikosov, and Leggett all did!
Can you think of others?

However, mean-field theory does have its limitations.
It is usually quantitatively wrong. It often gives unreliable values for transition temperatures. In spatial dimensions less than four, mean-field theory gives the wrong values for the critical exponents near a phase transition.

An even bigger problem is that mean-field can be qualitatively wrong.
For many models (e.g. the Ising model or Heisenberg model) mean-field theory always gives a transition from a disordered to an ordered phase at a non-zero temperature.
However, in one dimension the Ising model has no phase transition in one dimension. For a Heisenberg ferromagnet or antiferromagnet, there is no transition at finite temperature in two dimensions.
The Mermin-Wagner theorem states that in two dimensions a superconductor or superfluid never has long-range order at finite temperature. Instead, there is a Kosterlitz-Thouless transition, to a distinct state of matter, with power-law correlations.

Mean-field theory can also fail to predict the existence of states of matter. For example, for Hubbard models, mean-field theory can produce several states: a Fermi liquid metal, a ferromagnetic metal, an antiferromagnetic metal, and a spin-density-wave insulator. But it is quite possible the model also can have non-magnetic Mott insulating phases, superconductivity, non-Fermi liquid metals, and pseudogap states.

In the next post, I will discuss some issues that arise in mean-field theories used in modeling the COVID-19 epidemic.

The quantum physics of life in red and green

Life is truly amazing!
Life is beautiful!
...and it involves quantum many-body physics...

There is a beautiful (short) review
Heme: From quantum spin crossover to oxygen manager of life 
Kasper Kepp

The article involves a plethora of topics that I have discussed before on this blog. I have included relevant links.

Kepp starts with the unique (chemically fine-tuned) properties of both iron and porphyrin that enable them to play a central role in two of the most important processes in life: respiration and photosynthesis. He has a beautiful paragraph (perhaps in the style of Roald Hoffmann):

Such ligand-field transitions of iron in porphyrin were familiar to our ancestors as the characteristic red color of blood that largely defines the human psychological and cultural connotations of the color representing courage, war, danger, and suffering. 

Incidentally, pi-pi* transitions within the porphyrin-derived chlorophylls are also responsible for the green color of plants, associated with nature, life and hope, so the reader may perhaps agree that porphyrin has had vast (but alas! rarely appreciated) cultural consequences.

The oxygen molecule is a spin triplet.
Iron(II) porphyrin is in a triplet spin state (S=1). The Fe(II) is a d6 configuration in a D_4h crystal field.
When they bind together the ground state is a spin-singlet.

There are two fundamental quantum chemistry questions that are discussed.

1. What is the electronic structure (many-body wave function) of the ground state for oxygen bound to heme?

2. What is the mechanism for the ``spin-forbidden'' transition of the oxygen binding?

The first question has a long history. Like almost anything important and profound in quantum chemistry it goes back to Linus Pauling! In 1936 Pauling and Coryell argued that the ground state is

essentially a neutral O=O binding with two of its electrons to iron to produce a formally iron(II) if both the bonding electrons were confined to O2, corre- sponding to the non-bonding limit of neutral parts, but a formally iron(I) if the Fe–O bond were to be considered covalent. 

In 1960, McClure suggested a valence-bond formulation based on triplet–triplet coupling, which is appealing by the low promotion energies required to access these states, rather than the singlet states. In 1964, Weiss suggested, based on analogy to chemical reactions in aqueous solution, that the true ferrous hemeO2 adduct was mainly of the superoxo-iron(III) type caused by ‘‘electron transfer” from iron to O2. 

Goddard and Olafson suggested an ozone model of the adduct in 1975 which emphasized the four-electron three-center bond with maintained triplet state of dioxygen as in the McClure model with less electronic reorganization to explain the reversible binding. 

In 1977, Pauling maintained his original view again, the same year that Huynh, Case, and Karplus did a first attempt to bridge these views by performing early quantum chemical calculations that diplomatically emphasized the importance of both Weiss and Pauling resonance forms. 

However, interpretation depends on model language, orbital localization, and transformation between valence bond and orbital formalisms:  

In terms of molecular orbital theory, the wave function was a multi-configurational state dominated by the Pauling configuration; however, if one uses valence bond theory considerations, it can be interpreted as having large Weiss character. Thus, the multi-configurational state produced from CASPT2 is interpreted differently by different models. This partly explains why the trenches were so deeply dug during the exchange between Pauling, Goddard, McClure, and Weiss; all were right, and all were wrong. 

This is just another example of unnecessary conflicts about valence bond vs. molecular orbital (VB vs. MO). 

In terms of valence structures, the ground state was summarized by Shaik and Chen as having contributions from both Weiss, Pauling, and McClure forms, the first .. dominating. 

Ironically DFT ends up providing a useful language after all! 

The charge assignments to O2 are very dependent on calculation scheme, and both the orbitals, valence structures, and atomic charges that defined the Weiss-Pauling debate are non-observable. In contrast, the electron density is observable as are the geometries and spectroscopic data...

Molecular orbitals are not physical observables but calculational constructs. MO's don't exist.

In different words, one can take a many-body wave-function and make a linear unitary transformation of the molecular orbitals. The Slater determinants do not change. [The value of a determinant is invariant to a change of basis.]

Now. Question 2.
What is the mechanism for the ``spin-forbidden'' transition of the oxygen binding?

Kepp talks about spin-orbit coupling and the fact that it is small for oxygen, motivating a discussion of a "broad crossing mechanism".  However, I am not sure this is relevant. I don't see the binding as necessarily spin forbidden. As the oxygen approaches the heme the two triplet states can mix to form a total spin singlet.
This is analogous to bringing two hydrogen atoms (each of which is spin 1/2) together to form a hydrogen molecule (which is spin zero). A multi-configurational wavefunction has no problem with this. But DFT-based approximations, which use a single determinant cannot describe this smooth crossover.

Other things of particular interest to me that are discussed in the review include the central role of back bonding and the success of the TPSSh functional in DFT calculations for organometallics.

Unfortunately, the review does not mention recent work by Weber et al, applying DMFT to the problem of oxygen binding to haemoglobin.

Spin-crossover in geophysics

Most of my posts on spin-crossover materials have been concerned with organometallic compounds. However, this phenomena can also occur in inorganic materials. Furthermore, it may be particularly relevant in geophysics. A previous post discussed how strong electron correlations may play a role in geomagnetism and DMFT calculations have given some insight.

A nice short overview and introduction is
Electronic spin transition of iron in the Earth's deep mantle 
Jung‐Fu Lin Steven D. Jacobsen Renata M. Wentzcovitch

[It contains the figure below]
The main material of interest is magnesiowüstite, an alloy of magnesium and iron oxide,
(Mg1−xFex)O



Experimental studies and DFT calculations suggest that as the pressure increases the iron ions undergo a transition from high spin to low spin. The basic physics is that the pressure reduces the Fe-O bond lengths which increases the crystal field splitting.
In geophysics, the pressure increases as one goes further underground.

DFT+U calculations are reported in
Spin Transition in Magnesiowüstite in Earth’s Lower Mantle 
Taku Tsuchiya, Renata M. Wentzcovitch, Cesar R. S. da Silva, and Stefano de Gironcoli

The main result is summarised in the figure below.

There is a smooth crossover from high spin to slow spin, as is observed experimentally. However, it should be pointed out that this smoothness (versus a first-order phase transition with hysteresis) is built into the calculation (i.e. assumed) since the low spin fraction n is calculated using a single site model.  On the other hand, the interaction between spins may be weak because this is a relatively dilute alloy of iron (x=0.1875).
Also, the vibrational entropy change associated with the transition is not included. In organometallics, this can have a significant quantitative effect on the transition.

The elastic constants undergo a significant change with the transition. This is important for geophysics because these changes affect phenomena such as the transmission of earthquakes.

Abnormal Elasticity of Single-Crystal Magnesiosiderite across the Spin Transition in Earth’s Lower Mantle 
Suyu Fu, Jing Yang, and Jung-Fu Lin

A previous post considered changes in the elasticity and phonons in organometallic spin-crossover. Unfortunately, that work did not have the ability to resolve different elastic constants.

Phonons in organic molecular crystals.

In any crystal the elementary excitations of the lattice are phonons. The dispersion relation for these quasi-particles relates their energy and momentum. This dispersion relation determines thermodynamic properties such as the temperature dependence of the specific heat and plays a significant role in electron-phonon scattering and superconductivity in elemental superconductors. A nice introduction is in chapter 13 of Marder's excellent text. [The first two figures below are taken from there].

The dispersion relation is usually determined in at least one of three different ways.

1. The classical mechanics of balls and harmonic springs, representing atoms and chemical bonds, respectively. One introduces empirical parameters for the strengths of the bonds (spring constants).

2. First-principles electronic structure calculations, often based on density functional theory (DFT). This actually just determines the spring constants in the classical model.

3. Inelastic neutron scattering.

The figure below shows the dispersion relations for a diamond lattice using parameters relevant to silicon, using method 1. I find it impressive that this complexity is produced with only two parameters.

Furthermore, it produces most of the details seen in the dispersion determined by method 3. (Squares in the figure below.) which compare nicely with method 2. (solid lines below).

What about organic molecular crystals?
The following paper may be a benchmark.

Phonon dispersion in d8-naphthalene crystal at 6K 
I Natkaniec, E L Bokhenkov, B Dorner, J Kalus, G A Mackenzie, G S Pawley, U Schmelzer and E F Sheka

The authors note that method 3. is particulary challenging for three reasons.

• The difficulties in growing suitable single-crystal samples. 
• The high energy resolution necessary to observe the large number of dispersion curves (in principle there are 3NM modes, where N is the number of atoms per molecule and M is the number of molecules per unit cell). 
• The high momentum resolution necessary to investigate the small Brillouin zone (due to the large dimensions of the unit cell).

The figure below shows their experimental data for the dispersions. The solid lines are just guides to the eye.

The authors also compare their results to method 1. However, the results are not that impressive, partly because it is much harder to parameterise the intermolecular forces, which are a mixture of van der Waals and pi-pi stacking interactions. Hence, crystal structure prediction is a major challenge.

A recent paper uses method 2. and compares the results of three different DFT exchange-correlation functionals to the neutron scattering data above.
Ab initio phonon dispersion in crystalline naphthalene using van der Waals density functionals
Florian Brown-Altvater, Tonatiuh Rangel, and Jeffrey B. Neaton

What I would really like to see is calculations and data for spin-crossover compounds.

A critique of DFT calculations for spin crossover materials

A basic question concerning spin crossover compounds is what are the energy difference and entropy difference between the low spin (LS) and high spin (HS) states.

The relative magnitude of these two quantities determines the crossover temperature from the LS to HS state.

From experiment typical values of the energy difference Delta H are of the order of 1-5 kcal/mol (4-20 kJ/mol). Entropy differences are typically about 30-60 kJ/mol/K. (See table 1 in the Kepp paper below).
This relatively small difference in energy presents a challenge for computational quantum chemistry,
such as calculations based on density functional theory, because of the strong electron correlations associated with the transition metal ions,

Over the past few years some authors have done nice systematic studies of a wide range of compounds with a wide range of DFT exchange-correlation (XC) functionals. Here I will focus on two papers.

Benchmarking Density Functional Methods for Calculation of State Energies of First Row Spin-Crossover Molecules 
Jordi Cirera, Mireia Via-Nadal, and Eliseo Ruiz

Theoretical Study of Spin Crossover in 30 Iron Complexes 
Kasper P. Kepp

First, these studies are refreshing and important. Too many computational chemistry calculations are dubious because they do not do systematics. 
Here I will just discuss the first paper.

Cirera et al. use 8 different XC functionals to study 20 different compounds. They find that only one (!) functional (TPSSh) correctly gives a low spin ground state for all the compounds, i.e. Delta H is positive.

The figure below nicely summarises the results.

Before one gets too excited that one has now found the "right" functional, one should note that when one uses TPSSh to calculate the crossover temperature there is little correlation with the experimental values.

To put all this in a broader context consider the hierarchal figure below which is in the spirit of the metaphor of Jacob's ladder proposed by John Perdew. [The figure is from here]. However, I do not think Jacob's ladder is the best Biblical metaphor.

This highlights the ad hoc nature of DFT based calculations and that one is a long way from anything that should seriously be considered to be a true ab initio calculation.

It should also be noted that all these calculations are for a single molecule in vacuum. However, the experiments are in the solid state (or solution) and so the energetics can be shifted by electrostatic screening and/or solvation. The crossover temperature (which can become a first-order phase transition) may also be shifted by intermolecular elastic interactions.

Strategies for minimal effective Hamiltonians

An important step in understanding any class of complex materials is to find/discover the simplest possible effective Hamiltonian that can be used to describe the main properties of interest (e.g. a phase diagram).

Doing this well is a non-trivial and subjective process. I am thinking about this because I am currently trying to figure out the appropriate Hamiltonian for spin-crossover compounds.

Here are some key elements of the process. 

"Simplest possible" means having the fewest possible degrees of freedom and parameters.

1. What are the key degrees of freedom (molecular orbitals, vibrations, spins, ...)?

2. What are the key interactions and the associated Hamiltonian?

3. What approximation scheme can be used to calculate properties of the many-body Hamiltonian (ground state, thermodynamics, electronic, magnetic, ...)?

4. How do the calculated properties compare to experiment?

5. Can we estimate the values of the Hamiltonian parameters from the comparison of the calculated properties with experiments? 

6. Can we estimate the values of the Hamiltonian parameters from ab initio electronic structure methods, such as those based on density functional theory (DFT)?

Inevitably, things do not work out perfectly, sometimes qualitatively and always somewhat quantitatively. Then one has to face the difficult task of deciding what the problem is and what the next step is. There are several options.

A. There are some missing degrees of freedom in the original Hamiltonian.

B. There are some missing interactions.

C. The approximation scheme used to calculate properties was not reliable enough.

D. There is a problem with the experiments.

E. This is really the best one can hope to do and you should move on to other problems. i.e, know when to quit and face the law of diminishing returns.

This plethora of options is why falsifiability is so hard in the theory of strongly correlated electron materials. But, it does not mean we should give up on it.

The flow diagram below is one way of looking at the process. Some people like the picture. Others do not. As usual, real science is not quite so algorithmic.

First-order transitions and critical points in spin-crossover compounds

An interesting feature of spin-crossover compounds is that the transition from low-spin to high-spin with increasing temperature is usually a first-order phase transition. This is associated with hysteresis and the temperature range of the hysteresis varies significantly between compounds.
If there was no interaction between the transition metal ions the transition would be a smooth crossover. This is nicely illustrated in a figure taken from the paper below.

Abrupt versus Gradual Spin-Crossover in FeII(phen)2(NCS)2 and FeIII(dedtc)3 Compared by X-ray Absorption and Emission Spectroscopy and Quantum-Chemical Calculations 
Stefan Mebs, Beatrice Braun, Ramona Kositzki, Christian Limberg, and Michael Haumann

For the first compound, the transition is abrupt [much earlier work found a narrow hysteresis region of about 0.15 K]. For the second compound, the transition is a crossover.

The authors fit their data to an empirical equation that has a parameter n, describing the "interactions". You have to read the Supplementary Material to find the details. This equation cannot describe hysteresis.

 However, there is an elegant analytical theory going back to a paper by Wajnflasz and Pick from 1971. This is nicely summarised in the first section of a paper by Kamel Boukheddaden, Isidor Shteto, Benoit Hôo, and François Varret.

The system can be described by the Ising model

where the Ising spin denotes the high- and low-spin states. Delta is the energy difference between them and ln g the entropy difference.
The mean-field Hamiltonian for q nearest neighbours is

There are two independent dimensionless variables, d and r. Solving for the fraction of high-spin states (HS) versus temperature gives the graphs below for different values of d.

The vertical arrows show the hysteresis region for a specific value of d=2. 

As d increases the hysteresis region gets smaller. Above the critical value of d=r/2, the crossover temperature T0=Delta/ln g is larger than the mean-field critical temperature Tc= qJ, and the transition is no longer first-order but a crossover.

Using DFT-based quantum chemistry, the authors calculate the change in vibrational frequencies and the associated entropy change for the SCO transition in a single molecule. The values for compounds 1 and 2 are 0.68  and 0.21 meV/K, respectively. The spin entropy changes are 0.21 and 0.22 meV/K respectively. The total entropy changes are thus 0.89 and 0.43 meV/K respectively. The values of Delta are 175 and 125 meV, respectively. The corresponding crossover temperatures are 210 and 360 K, compared to the experimental values of 176 and 285 K.

If we assume that J is roughly the same for both compounds, then the fact that the entropy change is half as big for compound 2, means r is twice as big. This naturally explains why the second compound has a smooth crossover, compared to the first, which is very close to the critical point.

Square ice on graphene?

As I have written many times before, water is fascinating, a rich source of diverse and unusual phenomena, and an unfortunate source of spurious research reports.
Polywater is the classic example of the latter.
I find the physics particularly interesting because of the interplay of hydrogen bonding and quantum nuclear effects such as zero-point motion and tunneling.

There is a fascinating paper
Polymorphism of Water in Two Dimensions
Tanglaw Roman and Axel Groß

The paper was stimulated by a Nature paper that claimed to experimentally observe square ice inside graphene nanocapillaries. Such a square structure is in contrast to the hexagonal structure found in regular three-dimensional ice.
Subsequent, theoretical calculations claimed to support this observation of square ice.
Here the authors use DFT-based methods to calculate the relative energies of a range of two-dimensional structures for free-standing sheets of water (both single layer and bilayers) and for sheets bounded by two layers of graphene.

The figure below summarises the authors results for free-standing layers showing how the relative stability of the different water structures depends on the area density of water molecules [which varies the length and strength of the hydrogen bonds].

On the science side, there are several interesting questions arise.
How much do the results depend on the choice of DFT functional used [RPBE with dispersion corrections]?
Would inclusion of the nuclear zero-point energy modify the relative stability of some of the structures, as it does for the water hexamer?
Quantum nuclear effects are particularly important when the hydrogen bond length [distance between oxygen atoms] is about 2.4 Angstroms. [I am not quite sure what area density this corresponds to for the different structures].

On the sociology side, this paper is another example of a distressingly common progression:
1. A paper in a luxury journal reports an exotic and exciting new result.
2. More papers appear, some supporting and some raising questions about the result.
3. A very careful analysis reported in a solid professional journal shows the original claim was largely wrong. This paper attracts few citations because the community has moved on to the latest exciting new "discovery" reported in a luxury journal.

I thank Tanglaw Roman for helpful discussions about his paper.

Quantum spin liquid on the hyper-honeycomb lattice

Two of my UQ colleagues have a nice preprint that brings together many fascinating subjects including strong electron correlations and MOFs. Again it highlights an ongoing theme of this blog, how chemically complex materials can exhibit interesting physics. A great appeal of MOFs is the possibility of using chemical "tuneability" to design materials with specific physical properties.

A theory of the quantum spin liquid in the hyper-honeycomb metal-organic framework [(C2H5)3NH]2Cu2(C2O4)3 from first principles 
A. C. Jacko, B. J. Powell

What is a hyper-honeycomb lattice?
It is a three-dimensional version of the honeycomb lattice.
A simple tight-binding model on the lattice has Dirac cones, just like graphene.

The preprint is a nice example how one can start with a structure that is chemically and structurally complex and then use calculations based on Density Functional Theory (DFT) to derive a "simple" effective Hamiltonian (in this case an antiferrromagnetic Heisenberg model of coupled chains) to describe the low-energy physics of the material.

We construct a tight-binding model of [(C2H5)3NH]2Cu2(C2O4)3 from Wannier orbital overlaps. Including interactions within the Jahn-Teller distorted Cu-centered eg Wannier orbitals leads to an effective Heisenberg model. The hyper-honeycomb lattice contains two symmetry distinct sublattices of Cu atoms arranged in coupled chains. One sublattice is strongly dimerized, the other forms isotropic antiferromagnetic chains. Integrating out the strongest (intradimer) exchange interactions leaves extremely weakly coupled Heisenberg chains, consistent with the observed low temperature physics.

There is some rather subtle physics involved in the superexchange processes that determine the magnitude of the antiferromagnetic interactions J between neighbouring spins. In particular, there are destructive quantum interference effects that reduce one of the J's by an order of magnitude and increases another by an order of magnitude. To illustrate this effect, the authors also evaluate the J's when one flips the sign of some of the matrix elements in the tight-binding model. Similar subtle physics has also been observed in different families of organic charge transfer salts.

As an aside, there is some similarity (albeit many differences) with the basic chemistry of the insulating phase of cuprates: the parent compound involves a lattice of copper ions (d9) where there are three electrons in eg orbitals that are split by a Jahn-Teller distortion. The differences here are first, that the interactions between the frontier orbitals on the Cu sites is not via virtual processes involving oxygen p-orbitals but rather via pi-orbitals on the oxalate bridging orbitals. Second, the lattice of Cu orbitals is not a square but the hyper-honeycomb lattice.

The preprint is motivated by a recent experimental paper in JACS
Quantum Spin Liquid from a Three-Dimensional Copper-Oxalate Framework 
Bin Zhang, Peter J. Baker, Yan Zhang, Dongwei Wang, Zheming Wang, Shaokui Su, Daoben Zhu, and Francis L. Pratt

Conducting metallic-organic frameworks

Thanks to the ingenuity of synthetic chemists metallic-organic frameworks (MOFs) represent a fascinating class of materials with many potential technological applications.
Previously, I have posted about spin-crossover, self-diffusion of small hydrocarbons, and the lack of reproducibility of CO2 absorption measurements in these materials.

At the last condensed matter theory group meeting we had an open discussion about this JACS paper.
Metallic Conductivity in a Two-Dimensional Cobalt Dithiolene Metal−Organic Framework 
Andrew J. Clough, Jonathan M. Skelton, Courtney A. Downes, Ashley A. de la Rosa, Joseph W. Yoo, Aron Walsh, Brent C. Melot, and Smaranda C. Marinescu

The basic molecular unit is shown below. These molecules stack on top of one another, producing a layered crystal structure. DFT calculations suggest that the largest molecular overlap (and conductivity) is in the stacking direction.
Within the layers the MOF has the structure of a honeycomb lattice.

The authors measured the resistivity of several different samples as a function of temperature. The results are shown below. The distances correspond to the size of the compressed powder pellets.

Based on the observation that the resistivity is a non-monotonic function of temperature they suggest that as the temperature decreases there is a transition from an insulator to a metal. Since there is no hysteresis they rule out a first-order phase transition, as is observed in vanadium oxide, VO2.
They claim that the material is an insulator about about 150 K, based on fitting the resistivity versus temperature to an activated form, deducing an energy gap of about 100 meV. However, one should note the following.

1. It is very difficult to accurately measure the resistivity of materials, particularly anisotropic ones. Some people spend their whole career focussing on doing this well.

2. Measurements on powder pellets will contain a mixture of the effects of the crystal anisotropy, random grain directions, intergrain conductivity, and contact resistances. This is reflected in how sample dependent the results are above.

3. The measured resistivity is orders of magnitude larger than the Mott-Ioffe-Regel limit. suggesting the samples are very "dirty" or one is not measuring the intrinsic conductivity or this is a very bad metal due to electron correlations.

4. It is debatable whether one can deduce activated behaviour from only an order of magnitude variation in resistance, due to the narrow temperature range considered.

The temperature dependence of the magnetic susceptibility is shown below, and taken from the Supplementary material.

The authors fit this to a sum of several terms, including a constant term and a Curie-Weiss term. The latter gives a magnetic moment associated with S=1/2, as expected for the cobalt ions, and an antiferromagnetic exchange interaction J ~ 100 K. This is what you expect if the system is a Mott insulator or a very bad metal, close to a Mott transition.

Again, there a few questions one should be concerned about.

1. How does this relate to the claim of a metal at low temperatures?

2. The problem of curve fitting. Can one really separate out the different contributions?

3. Are the low moments due to magnetic impurities?

The published DFT-based calculations suggest the material should be a metal because the bands are partially full. Electron correlations could change that. The band structure is quasi-one-dimensional with the most conducting direction perpendicular to the plane of the molecules.

All these questions highlight to me the problem of multi-disciplinary papers. Should you believe physical measurements published by chemists? Should you believe chemical compositions claimed by physicists? Should you believe theoretical calculations performed by experimentalists? We need each other and due diligence, caution, and cross-checking.

Having these discussions in group meetings is important, particularly for students to see they should not automatically believe what they read in "high impact" journals?

An important next step is to come up with a well-justified effective lattice Hamiltonian.

Observation of renormalised quasi-particle excitations

A central concept of quantum-many body theory is that of coherent quasi-particles. Their key property is a well-defined relationship between energy and momentum (dispersion relation). Prior to the rise of ARPES (Angle-Resolved Photo-Emission Spectroscopy) over the past three decades, the existence of electronic quasi-particles was only inferred indirectly.

A very nice paper just appeared which shows a new way of measuring quasi-particle excitations in a
strongly correlated electron system. Furthermore, the experimental results are compared quantitatively to state-of-the-art theory, showing several subtle many-body effects.

Coherent band excitations in CePd3: A comparison of neutron scattering and ab initio theory 
Eugene A. Goremychkin, Hyowon Park, Raymond Osborn, Stephan Rosenkranz, John-Paul Castellan, Victor R. Fanelli, Andrew D. Christianson, Matthew B. Stone, Eric D. Bauer, Kenneth J. McClellan, Darrin D. Byler, Jon M. Lawrence

The mixed valence compound studied is of particular interest because with increasing temperature it exhibits a crossover from a Fermi liquid with coherent quasi-particle excitations to incoherent excitations, an example of a bad metal.

The figure below shows a colour intensity plot of the dynamical magnetic susceptibility

at a fixed energy omega, and a function of the wavevector Q. The top three panels are from the calculations of DFT+DMFT (Density Functional Theory + Dynamical Mean-Field Theory).

The bottom three panels are the corresponding results from inelastic neutron scattering.
A and B [D and E] are both at omega=35 meV and in two different momentum planes. C [F] is at omega=55 meV.
The crucial signal of coherence (i.e. dispersive quasi-particles) is that the shift of the maxima between the G and R points at 35 meV to the M and X points at 55 meV.

It should be stressed that these dispersing excitations are not due to single (charged) quasi-particles, but rather spin excitations which are particle-hole excitations.

The figure below shows how the dispersion [coherence] disappears as the temperature is increased from 6 K (top) to 300 K (bottom). The solid lines are theoretical curves.

The figure below shows that the irreducible vertex corrections associated with the particle-hole are crucial to the quantitative agreement of theory and experiment. The top (bottom) panel in the figure below shows the calculation at low (high) temperatures. The black (blue) curves are with (without) vertex corrections. The red curves are a rescaling of the blue curves by a numerical factor.

The correction has two effects: First, it smooths out some of the fine structure in the energy dependence of the spectra while broadly preserving both the Q variation and the overall energy scale; and second, it produces a strong enhancement of the intensity that is both energy and temperature dependent, for example, by a factor of ~6.5 at w = 60 meV at 100 K. This shows that the Q dependence of the scattering is predomi- nantly determined by the one-electron joint density of states, as expected for band transitions, whereas the overall intensity is amplified by the strong electron correlations. 

This landmark study is only possible due to recent parallel advances in theory, computation, and experiment. 
On the theory side, it is not just DMFT but also including particle-hole interactions in DMFT.
On computation, it is new DMFT algorithms and increasing computer speed. 
On the experimental side, it is pulsed neutron sources, and improvements in the sensitivity and spatial and energy resolution of neutron detectors.

The challenge of applied research

Last friday we were fortunate to have David Sholl give a physics colloquium at UQ,
``What Does Quantum Mechanics Have To Do With The Chemical Industry? Reflections On A Journey From Pure To Applied Research.''
Here are the slides.

David has a background in theoretical physics and has been particularly successful at using atomistic simulations to study problems that chemical engineers care about. He is co-author of a book, Density Functional Theory: A Practical Introduction
His three main points in the talk were

• Applied research is worth doing and is intellectually satisfying
• Applied research relies on fundamental insights 
• How to waste time and money doing applied research

The piece of science I found most interesting was the figure below which shows how the calculated self-diffusion constant D of small hydrocarbons in a zeolitic imidazolate framework varies with the size of the hydrocarbon molecule.
Note how D varies over 14 orders of magnitude.

Some of the key physics is that this large variation arises because the diffusion constant is essentially determined by the activation energy associated with the transfer of a molecule through the molecular hole between adjacent pores. When the molecular size is comparable to the hole size, D rapidly diminishes because of steric effects.
It would be nice to have "simple" theory of the correlation.

The figure is taken from the paper
Temperature and Loading-Dependent Diffusion of Light Hydrocarbons in ZIF-8 as Predicted Through Fully Flexible Molecular Simulations 
Ross J. Verploegh, Sankar Nair, and David S. Sholl

Computational density functional theory (DFT) in a nutshell

My recent post, Computational Quantum Chemistry in a nutshell, was quite popular. There are two distinct approaches to computational approaches: those based on calculating the wavefunction, which I described in that post, and those based on calculating the local charge density [one particle density matrix of the many-body system]. Here I describe the latter which is based on density functional theory (DFT). Here are the steps and choices one makes.

First, as for wave-function based methods, one assumes the Born-Oppenheimer approximation, where the atomic nuclei are treated classically and the electrons quantum mechanically.

Next, one makes use of the famous (and profound) Hohenberg-Kohn theorem which says that the total energy of the ground state of a many-body system is a unique functional of the local electronic charge density, E[n(r)]. This means that if one can calculate the local density n(r) one can calculate the total energy of the ground state of the system. Although this is an exact result, the problem is that one needs to know the exchange-correlational functional, and one does not. One has to approximate it.

The next step is to choose a particular exchange-correlation functional. The simplest one is the local density approximation [LDA] where one writes E_xc[n(r)] = f(n(r)), where f(x) is the corresponding energy for a uniform electron gas with constant density x. Kohn and Sham showed that if one minimises the total energy as a function of n(r) then one ends up with a set of eigenvalue equations for some functions phi_i(r) which have the identical mathematical structure to the Schrodinger equation for the molecular orbitals that one calculates in a wave-function based approach with the Hartree-Fock approximation. However, it should be stressed that the phi_i(r) are just a mathematical convenience and are not wave functions. The similarity to the Hartree-Fock equations means the problem is not just computationally tractable but also relatively cheap.

When one solves the Kohn-Sham equations on the computer one has to choose a finite basis set. Often they are similar to the atomic-centred basis sets used in wave-function based calculations. For crystals, one sometimes uses plane waves. Generally, the bigger and the more sophisticated and chemical appropriate the basis set, the better the results.

With the above uncontrolled approximations, one might not necessarily expect to get anything that proximates reality (i.e. experiment). Nevertheless, I would say the results are often surprisingly good. If you pick a random molecule LDA can give a reasonable answer (say within 20 per cent) of the geometry, bond lengths, heats of formation, and vibrational frequencies... However, it does have spectacular failures, both qualitative and quantitative, for many systems, particularly those involving strong electron correlations.

Over the past two decades, there have been two significant improvements to LDA.
First, the generalised gradient approximation (GGA) which has an exchange-correlation functional that allows for the spatial variations in the density that are neglected in LDA.
Second, hybrid functionals (such as B3LYP) which contain a linear combination of the Hartree- Fock exchange functional and other functionals that have been parametrised to increase agreement with experimental properties.
It should be stressed that this means that the calculation is no longer ab initio, i.e. one where you start from just Schrodinger's equation and Coulomb's law and attempts to calculate properties.

It should be stressed that for interesting systems the results can depend significantly on the choice of exchange-correlational functional. Thus, it is important to calculate results for a range of functionals and basis sets and not just report results that are close to experiment.

DFT-based calculations have the significant advantage over wave-function based approaches that they are computationally cheaper (and so are widely used). However, they cannot be systematically improved [the dream of Jacob's ladder is more like a nightmare], and become problematic for charge transfer and the description of excited states.

Computational quantum chemistry in a nutshell

To the uninitiated (and particularly physicists) computational quantum chemistry can just seem to be a bewildering zoo of multiple letter acronyms (CCSD(T), MP4, aug-CC-pVZ, ...).

However, the basic ingredients and key assumptions can be simply explained.

First, one makes the Born-Oppenheimer approximation, i.e. one assumes that the positions of the N_n nuclei in a particular molecule are a classical variable [R is a 3N_n dimensional vector] and the electrons are quantum. One wants to find the eigenenergy of the N electrons. The corresponding Hamiltonian and Schrodinger equation is

The electronic energy eigenvalues E_n(R) define the potential energy surfaces associated with the ground and excited states. From the ground state surface one can understand most of chemistry! (e.g., molecular geometries, reaction mechanisms, transition states, heats of reaction, activation energies, ....)
As Laughlin and Pines say, the equation above is the Theory of Everything!
The problem is that one can't solve it exactly.

Second, one chooses whether one wants to calculate the complete wave function for the electrons or just the local charge density (one-particle density matrix). The latter is what one does in density functional theory (DFT). I will just discuss the former.

Now we want to solve this eigenvalue problem on a computer and the Hilbert space is huge, even for a simple molecule such as water. We want to reduce the problem to a discrete matrix problem. The Hilbert space for a single electron involves a wavefunction in real space and so we want a finite basis set of L spatial wave functions, "orbitals". Then there is the many-particle Hilbert space for N-electrons, which has dimensions of order L^N. We need a judicious way to truncate this and find the best possible orbitals.

The single particle orbitals can be introduced

where the a's are annihilation operators to give the Hamiltonian

These are known as Coulomb and exchange integrals. Sometimes they are denoted (ij|kl).
Computing them efficiently is a big deal.
In semi-empirical theories one neglects many of these integrals and treats the others as parameters that are determined from experiment.
For example, if one only keeps a single term (ii|ii) one is left with the Hubbard model!

Equivalently, the many-particle wave function can be written in this form.

Now one makes two important choices of approximations.

1. atomic basis set
One picks a small set of orbitals centered on each of the atoms in the molecule. Often these have the traditional s-p-d-f rotational symmetry and a Gaussian dependence on distance.

2. "level of theory"
This concerns how one solves the many-body problem or equivalently how one truncates the Hilbert space (electronic configurations) or equivalently uses an approximate variational wavefunction. Examples include Hartree-Fock (HF), second-order perturbation theory (MP2),  a Gutzwiller-type wavefunction (CC = Coupled Cluster), or Complete Active Space (CAS(K,L)) (one uses HF for higher and low energies and exact diagonalisation for a small subset of K electrons in L orbitals.
Full-CI (configuration interaction) is exact diagonalisation. This only possible for very small systems.

The many-body wavefunction contains many variational parameters, both the coefficients in from of the atomic orbitals that define the molecular orbitals and the coefficients in front of the Slater determinants that define the electronic configurations.

Obviously, one expects that the larger the atomic basis set and the "higher" the level of theory  (i.e. treatment of electron correlation) one hopes to move closer to reality (experiment). I think Pople first drew a diagram such as the one below (taken from this paper).

However, I stress some basic points.

1. Given how severe the truncation of Hilbert space from the original problem one would not necessarily to expect to get anywhere near reality. The pleasant surprise for the founders of the field was that even with 1950s computers one could get interesting results. Although the electrons are strongly correlated (in some sense), Hartree-Fock can sometimes be useful. It is far from obvious that one would expect such success.

2. The convergence to reality is not necessarily uniform.
This gives rise to Pauling points: "improving" the approximation may give worse answers.

3. The relative trade-off between the horizontal and vertical axes is not clear and may be context dependent.

4. Any computational study should have some "convergence" tests. i.e. use a range of approximations and compare the results to see how robust any conclusions are.