Angle-Dependent Magnetoresistance as a probe of Fermi surface properties in cuprates

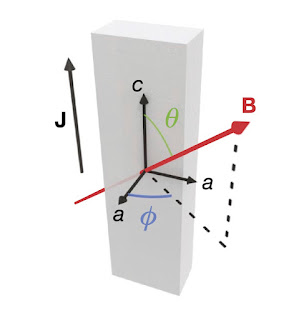
About twenty-five years ago I became interested in how the Fermi surface of the metallic state of organic charge-transfer salts could be mapped out by measuring the interlayer resistance as a function of the direction of a large applied magnetic field. [A nice review from 2004 is by Mark Kartsovnik]. Later this technique was used for a range of other metals including strontium ruthenate, iron pnictides, semiconductor heterostructures, and finally cuprates, mostly in the overdoped region.

For the cuprates, it was discovered that one could not only map out the shape of the intralayer Fermi surface, but also anisotropies in the scattering rate and the interlayer hopping integral. Of particular interest was the finding that the overdoped cuprates were not simple Fermi liquids, as usually claimed, but more like anisotropic marginal Fermi liquids.

It should be stressed that the Fermi surface information is extracted indirectly by comparing experimental curves of angle-dependence to calculations based on different models for the shape of the Fermi surface, anisotropies in the scattering rate, and interlayer hopping. Thus, there is a fair bit of curve fitting to determine the parameters of the model. However, when one has observations at several magnetic fields, temperatures, and curves for the angle dependence in all directions, there are a lot of constraints, and specific anisotropies tend to produce some specific qualitative features in the shapes of the curves. Examples are shown below, taken from the Nature paper referenced below.

Recently, measurements have been reported on samples of the cuprate Nd-LSCO 

[La1.6−xNd0.4SrxCuO4] at dopings of p=0.21 and p=0.24, lying on both sides of the putative quantum critical point at p=0.23. 

The differences between the ADMR at these two dopings are analysed quantitatively in a preprint, which claims to show that at p=0.21 the Fermi surface is reconstructed due to (pi,pi) ordering. This is important as it relates to the fundamental question as to the origin of the pseudogap state.

Fermi surface transformation at the pseudogap critical point of a cuprate superconductor

Yawen Fang, Gael Grissonnanche, Anaelle Legros, Simon Verret, Francis Laliberte, Clement Collignon, Amirreza Ataei, Maxime Dion, Jianshi Zhou, David Graf, M. J. Lawler, Paul Goddard, Louis Taillefer, B. J. Ramshaw

Submitted on 3 Apr 2020 (v1), last revised 26 Nov 2020 (v2)

Aside: There is also a Nature paper, Linear-in temperature resistivity from an isotropic Planckian scattering rate, by the same group that compares the p=0.24 observations to those on the overdoped cuprate Tl2201 [p=0..29]. The arxiv notes "substantial text overlap" between the preprint above and the preprint for the Nature paper. [Figure 2 in v1 of the preprint above is in the Nature paper].

Here I focus on the first preprint as it stimulated a nice theory preprint

Interpreting Angle Dependent Magnetoresistance in Layered Materials: Application to Cuprates

Seth Musser, Debanjan Chowdhury, Patrick A. Lee, T. Senthil

They present a strong case against the main claim of Fang et al. that their ADMR data supports a reconstructed Fermi surface for the p=0.21 system.

There are several nice things about this preprint.

1. It shows how one should be careful about interpreting ADMR

2. It highlights the possible role of an anisotropic quasi-particle weight, Z(phi), where phi denotes the position on the intralayer Fermi surface, not the direction of the field. Anisotropy can arise from correlation effects and or "coherence factors" associated with Fermi surface reconstruction due to an ordered state. 

2. In their modeling, Fang et al. did not include the effects of Z(phi) and Musser et al. show that when it is included the qualitative differences in the ADMR that they claim arise due to the ordered state do not appear.

3. The authors consider a "toy" model for which some analytical results can be obtained. 

4. This provides some physical insight into the origins of the different features in the data, such as the peak around theta=40 degrees [It is just the magic angle associated with the average radius of the Fermi surface] and how the behaviour near theta=90 degrees depends on the relative size of different parameters [see especially equation (16)].

5. What is happening in this material may not be generic to the cuprates. "The van Hove filling in Nd-LSCO is located between the two dopings, p = 0.21 and p = 0.24, respectively. Thus what was a large Fermi surface centered at the Γ-point on the overdoped side will become a Fermi surface centered at (π, π) on the underdoped side, assuming no reconstruction occurs"

6. The most important insight is at the beginning of Section V. When the value of of the interlayer hopping integral t_perp(phi) averaged over the Fermi surface, changes from non-zero to zero an upturn in the ADMR at low angles (i.e. fields almost parallel to the layers) to a downturn. This suggests an alternative explanation for the transition seen in the preprint.

7. It highlights the often overlooked fact that observation of ADMR is not conclusive evidence of a three-dimensional Fermi surface. Using the parameters from the experimental preprint gives typical values of t_perp * tau ~ 0.1, and so the materials are far from the regime of a coherent three-dimensional Fermi surface.

I have a few minor comments

a. Like many others, the authors incorrectly credit with Yamaji explaining the magic angles associated with ADMR. However, Yamaji's explanation is not the correct one because it involves quantised orbits, whereas the effect is semi-classical, as explained by Kartsovnik, Laukhin, Pesotskii, Schegolev, and Yakovenko. 

b. Investigation of the role of small closed orbits when the magnetic field is almost parallel to the layers is credited to Schofield and Cooper. However, there was earlier and more detailed work by Hanasaki et al. Albeit, both of these papers consider the clean high field limit and so are of debatable relevance.

c. It would be nice to know the status of Fang et al., preprint on which this paper is based, particularly as the first authors of both are in the same department.

Magnetic field induced (thermodynamic) phase transitions in graphite

One of the most common and reliable indicators of a phase transition into a new state of matter is anomalies (e.g. discontinuities or singularities) in thermodynamic properties such as specific heat capacity. This is how the superfluid phases of helium 4 and helium 3 were both discovered. Further transport experiments were required to show that the new states of matter were actually superfluids. This point was highlighted at the end of my last post.

In 2014, I wrote about the puzzling magnetoresistance of graphite and some experiments that were interpreted as evidence of a metal-insulator transition when the electrons are in the lowest Landau level of the graphene layers. This interpretation was partly motivated by theoretical predictions of charge density wave (CDW) transitions in this regime. I expressed some caution and skepticism about this interpretation, highlighting problems in other systems where magnetoresistance anomalies were given such interpretations.  I suggested that thermodynamic measurements should be performed.

In 2015, I highlighted similar issues, suggesting there is no metal-insulator transition in extremely large magnetoresistance materials, contrary to claims in luxury journals. Within two months my claim was shown to be correct.

I was delighted to recently learn from Benoit Fauque that he and his collaborators have now performed measurements of the specific heat of graphite in high magnetic fields.

Wide critical fluctuations of the field-induced phase transition in graphite 

Christophe Marcenat, Thierry Klein, David LeBoeuf, Alexandre Jaoui, Gabriel Seyfarth, Jozef Kačmarčík, Yoshimitsu Kohama, Hervé Cercellier, Hervé Aubin, Kamran Behnia, Benoît Fauqué

The figure below shows the ratio of the specific heat to temperature versus temperature for different values of the magnetic field. In an elemental metal, this would be the temperature and field-independent and equal to the specific heat coefficient gamma. The temperature dependence and peak at a particular temperature are reminiscent of the behaviour for a BCS superconductor or quasi-one-dimensional CDW transition.

I want to highlight a couple of nice things about this data and the analysis in the paper. First, the value of the specific heat coefficient at small fields is several orders of magnitude smaller than in an elemental metal (due to the low density and effective mass of charge carriers) and has a value consistent with band structure calculations. I presume that measuring such small values is a significant experimental achievement. 

Secondly, the linear increase in gamma with the magnetic field and the rate of increase are also consistent with band structure. These agreements increase confidence in the reliability of the measurements and their identification with electronic contributions to the specific heat. For context, the field of strongly correlated electron materials is littered with dubious identifications. An example concerns claims of spinons in an organic charge-transfer salt.

Most importantly the data above suggests that there is a thermodynamic phase transition and that the transition temperature increases with the magnetic field. The corresponding phase diagram can be compared to that suggested by the magnetoresistance measurements from 2014. This is done in the figure below.

The fact that the transition temperature deduced from the specific heat is tracking the anomalies in the earlier magnetoresistance measurements suggests the identification of the latter with a metal-insulator transition back in 2014 was correct. I am happy to be have been proven wrong! That's good science!

Phil Anderson (1923-2020): theoretical physicist extraordinaire

Phil Anderson died two weeks ago. There have been many obituaries, including at The New York Times, Not Even Wrong (Peter Woit), and Nanoscale Views (Doug Natelson). Few would argue that he was the greatest condensed matter theorist of the second half of the twentieth century. I would go further and suggest that he and Ken Wilson were the greatest theoretical physicists of the second half of the twentieth century. Anderson's scientific legacy extends far beyond condensed matter physics.

More than sixty posts on this blog include ``P.W. Anderson'' in the label. There is no doubt that Anderson is the largest intellectual influence on this blog.

Phil Anderson made incredibly diverse and valuable contributions to condensed matter physics (anti-ferromagnetism, localisation, weak localisation, magnetic impurities in metals, Kondo problem, poor mans scaling, superfluid 3He, spin liquids, RVB theory of superconductivity... ).

It is noteworthy that Anderson applied scaling to condensed matter before Wilson. In the late 1960s he wrote a series of papers on ``poor man's scaling" for the Kondo problem.

I can think of several significant and profound influences of Phil beyond condensed matter physics.

1. Codifying and elucidating the concept of emergence (and the limitations of reductionism) in all of science, in More is Different in 1972.
[Although it should be acknowledged that the word ``emergence'' does not appear in the article and that Michael Polanyi developed similar ideas about emergence earlier.]

2. Nambu referenced several papers by Anderson about superconductivity in his seminal papers on the mass of elementary particles and symmetry breaking.

3. Laying the groundwork for the Higgs boson in 1963 by connecting spontaneous gauge symmetry breaking and mass. 

4. Elucidating spin glasses in a way that was key to John Hopfield's development of a particular neural network and to the notion of a "rugged landscape", relevant in protein folding and evolution. Anderson described these connections nicely in two pages in Physics Today in 1990.

Phil had a significant influence on my own job/career trajectory. For my Princeton Ph.D. I worked with Jim Sauls on superfluid 3He, which Phil supported financially. He was on the committee for my Ph.D. thesis defense in 1988. In 1993, towards the end of a postdoc, my job prospects were extremely slim. Phil told me that he had been asked to review an application I made for a five-year research fellowship back in Australia. My success was probably based on a positive review from Phil. I regret that during my time as a graduate student I did not have the confidence to interact much with him. However, from about 1995 to 2002, I made a visit to Princeton practically every year and had some nice discussions with him. It was also fascinating to see the close personal and scientific relationship that Phil and N.P. Ong had; it was clearly mutually very beneficial.
One cryptic comment: ``look at the metal-insulator-metal tunneling theory from the 1960s" [I found Mahan has a nice discussion] set me on the right path to do the calculations in this paper, about angle-dependent-magnetoresistance oscillations in layered metals.

I highly recommend the Anderson anthologies (reprint collections), listed below in order of increasing technical difficulty.

More and Different: notes from a thoughtful curmudgeon.
It is a collection of essays on wide-ranging subjects: personal reminiscences, history, philosophy, sociology, science wars, ...
Some of these have been published before but many have not.

A Career in Theoretical Physics
Something amazing about this collection of papers is what is not in it; e.g. his papers on superfluid 3He with Brinkman, or on charge ordering and antiferromagnetism in ferrites.

Basic Notions of Condensed Matter Physics

Andrew Zangwill is working on a scientific biography of Phil Anderson. I am looking forward to reading.

Desperately seeking Weyl semi-metals. 2.

Since my previous post about the search for a Weyl semimetal in pyrochlore iridates (such as R2Ir2O7, where R=rare earth) read two more interesting papers on the subject.

Metal-Insulator Transition and Topological Properties of Pyrochlore Iridates 
Hongbin Zhang, Kristjan Haule, and David Vanderbilt

Using a careful DMFT+DFT study they are able to reproduce experimental trends across the series, R=Y, Eu, Sm, Nd, Pr, Bi.

They show that when the self energy due to interactions is included that the band structure is topologically trivial, contrary to the 2010 proposal based on DFT+U.

They also find that the quasi-particle weight is quite small (about 0.1 for R=Sm, Nd and 0.2 for Pr). This goes some way towards explaining the fact that the infrared conductivity gives an extremely small Drude weight (about 0.05 electrons per unit cell), a puzzle I highlighted in my first post.

Field-induced quantum metal–insulator transition in the pyrochlore iridate Nd2Ir2O7 
Zhaoming Tian, Yoshimitsu Kohama, Takahiro Tomita, Hiroaki Ishizuka, Timothy H. Hsieh, Jun J. Ishikawa, Koichi Kindo, Leon Balents, and Satoru Nakatsuji

The authors make much of two things.

First, the relatively low magnetic field (about 10 Tesla) required to induce the transition from the magnetic insulator to the metallic phase. Specifically, the relevant Zeeman energy is much smaller that the charge gap in the insulating phase.
However, one might argue that the energy scale one should be comparing to is the thermal energy associated with the magnetic transition temperature.

Second. the novelty of this transition.
However, in 2001 a somewhat similar transition was observed in the organic charge transfer salt, lambda-(BETS)2FeCl4. It is even more dramatic because it undergoes a field-induced transition from a Mott insulator to a superconductor. The physics is also quite similar in that it can also be described by Hubbard-Kondo model, where local moments are coupled to interacting delocalised electrons.

What are the biggest discoveries in solid state electronic technology?

Watching an excellent video about the invention of the transistor stimulated to me to think about other big discoveries and inventions in solid state technology.

Who would have thought that huge device would become the basis of an amazing revolution (both technological, economic, and even social...)?

In particular, which are the most ubiquitous ones?
For which devices did both theory and experiment play a role, as they did for the transistor?

I find it worthwhile to think about this for two reasons. First, this semester I am again teaching solid state physics and it is nice to motivate students with examples.
 Second, there is too much hype about basic research in materials and device physics, that glosses over the formidable technical and economic obstacles, to materials and devices becoming ubiquitous. Can history give us some insight as to what is realistic?

Here is a preliminary list of some solid state devices that are ubiquitous.

transistor

inorganic semiconductor photovoltaic cell

liquid crystal display

semiconductor laser

optical fiber

giant magnetoresistance used in hard disk drives

blue LED used in solid state lighting

lithium battery

Some of these feature in a nice brochure produced by the USA National Academy of Sciences.

Here are a few that might be on the list but I am not sure about as I think they are more niche applications with limited commercial success. Of course, that may change...

thermoelectric refrigerators

organic LEDs

superconductors (in MRI magnets and as passive filters in mobile phone relay towers )

Is graphene in any commercial device?

What would you add or subtract from the list?

Overdoped cuprates are marginal Fermi liquids

I am giving a talk tomorrow at the Superconductivity workshop at the Aspen Center for Physics.
Here is the current version of the slides. I will only cover the first half of the slides in the talk. The rest are from a longer version.

Often it is claimed that the overdoped cuprates are Fermi liquids. However, work with Jure Kokalj and Nigel Hussey, has shown that a wide range of experimental results can be described in terms of an electronic self energy that includes a marginal Fermi liquid component which has the same angular dependence as the pseudogap, i.e. there are cold spots near the nodes of the superconducting state.
What is particularly interesting to me is that this shows that even in the overdoped region one sees precursors of the distinct signatures of the strange metal and the pseudogap regions, that occur at optimal and underdoping, respectively.

The talk is largely based on this PRL and this PRB.

Deducing broken rotational symmetry from angle-dependent magnetoresistance

There is an interesting preprint
Broken rotational symmetry on the Fermi surface of a high-Tc superconductor 
B. J. Ramshaw, N. Harrison, S. E. Sebastian, S. Ghannadzadeh, K. A. Modic, D. A. Bonn, W. N. Hardy, Ruixing Liang, P. A. Goddard

They measure the interlayer magnetoresistance as function of magnetic field direction (see below) and from this deduce that the C4 symmetry of the crystal is broken to C2 in the charge density wave phase that occurs in the pseudogap region.

They then compare their experimental results to a calculation that uses a Fermi surface (that is reconstructed due to the CDW), a coherent three-dimensional Fermi surface, and a Boltzmann equation.

One might be concerned about the use of a three-dimensional Fermi surface because
a. the CDW correlation length between the layers is small
b. the interlayer charge transport is not necessarily coherent.

However, based on work I did long ago with Perez Moses and Malcolm Kennett [see for example this paper]. I think the theoretical results are robust to these concerns. What we showed is that for two contrasting situations shown below, the angle-dependent magnetoresistance is identical.

The top shows a coherent three-dimensional Fermi surface.
The bottom shows two layers that are coherently coupled together. The interlayer momentum is conserved in hopping between the layers.
One does not need coherence over more than two layers.

Another minor comment is that the authors did most of their calculations numerically. However, I think a lot can be done analytically using the expression below (from the Kennett paper) and simplifying for the case an isotropic scattering time (tau) and the low field limit (omega_c tau much less than one).

I thank Sam Lederer and Steve Hayden for bringing this work to my attention and asking about these issues.

Linear magnetoresistance in Dirac semi-metals turns out to be boring

An enduring theme on this blog is that one should always consider "boring" explanations for "surprising" experimental results before invoking the exotica beloved and promoted by luxury journals. An example was the extremely large magnetoresistance materials.

In most metals the magnetoresistance [change in electrical resistance with external magnetic field B] depends quadratically on the B.
The past few years there have been a plethora of papers about linear magnetoresistance in topological insulators, iron pnictide superconductors, and Dirac semi-metals. I wrote a post which discusses the issue and also links to an earlier post that considers different theoretical explanations.
Many of these papers, particularly those in the baby Natures, want to link the linear magnetoresistance to the Dirac cone and possibly the Berry geometric phase associated with it.

However, there are some critical and constructive papers. For example,
Magnetotransport of proton-irradiated BaFe2As2 and BaFe1.985Co0.015As2 single crystals 
D. A. Moseley, K. A. Yates, N. Peng, D. Mandrus, A. S. Sefat, W. R. Branford, and L. F. Cohen

By using proton-beam irradiation to change the defect scattering density, we find that the dependence of the magnitude of the linear magnetoresistance on scattering quite clearly contravenes this prediction [of Abrikosov's quantum model].

There is a nice paper that gives a rather mundane explanation for the experiments.
Linear magnetoresistance in metals: Guiding center diffusion in a smooth random potential
Justin C. W. Song, Gil Refael, and Patrick A. Lee

We predict that guiding center (GC) diffusion yields a linear and nonsaturating (transverse) magnetoresistance in 3D metals. Our theory is semiclassical and applies in the regime where the transport time is much greater than the cyclotron period and for weak disorder potentials which are slowly varying on a length scale much greater than the cyclotron radius. Under these conditions, orbits with small momenta along magnetic field B are squeezed and dominate the transverse conductivity. When disorder potentials are stronger than the Debye frequency, linear magnetoresistance is predicted to survive up to room temperature and beyond. We argue that magnetoresistance from GC diffusion explains the recently observed giant linear magnetoresistance in 3D Dirac materials.

In their calculations the Berry phase plays no role.

There is no metal-insulator transition in extremely large magnetoresistance materials. II

Two months ago I made this claim. I made some specific suggestions as to how one could quantitatively analyse the experimental data to support the claim. The same day of my post I received an email from Zhili Xiao with a copy of a submitted manuscript that had already done exactly what I suggested. The paper has now been published:

Origin of the turn-on temperature behavior in WTe2 
Y. L. Wang, L. R. Thoutam, Z. L. Xiao,  J. Hu, S. Das, Z. Q. Mao, J. Wei, R. Divan, A. Luican-Mayer, G. W. Crabtree, and W. K. Kwok

Below I show the relevant Kohler plot.

This is consistent with the simple idea that the origin of the magnetoresistence is simply the Lorentz force, the same as in elemental metals such as copper and zinc!
No exotic physics is required.

There is no metal-insulator transition in extremely large magnetoresistance materials

There is currently a lot of interest in layered materials with extremely large magnetoresistance [XMR], partly stimulated by a Nature paper last year.
The figure below shows the data from that paper, which is my main focus in this post.

A recent PRL contains the following paragraph

A striking feature of the XMR in WTe2 is the turn-on temperature behavior: in a fixed magnetic field above a certain critical value Hc, a turn-on temperature T∗ is observed in the R(T) curve, where it exhibits a minimum at a field-dependent temperature T∗. At T<T∗, the resistance increases rapidly with decreasing temperature while at T>T∗, it decreases with temperature [2]. This turn-on temperature behavior, which is also observed in many other XMR materials such as graphite [19,20], bismuth [20], PtSn4 [21], PdCoO2 [22], NbSb2 [23], and NbP [24], is commonly attributed to a magnetic-field-driven metal-insulator transition and believed to be associated with the origin of the XMR [10,19,20,23,25].

My main point is that this temperature dependence and the "turn-on" has a very simple physical explanation: it is purely a result of the strong temperature dependence of the charge carrier mobility (scattering rate), which is reflected in the temperature dependence of the zero field resistance.
It is completely unnecessary to invoke a metal-insulator transition.
The "turn on" is really a smooth crossover.
I made this exact same point in a post last year about PdCoO2  and in this old paper.

Following the discussion [especially equation (1)] in the Nature paper, consider a semi-metal that has equal density of electrons and holes (n=p). For simplicity assume they have the same temperature dependent mobility mu(T). Then the total resistivity in a magnetic field B is given by

Differentiating this expression with respect to temperature T, for fixed B, one finds that the resistance is a minimum, at a temperature T* given by

Further justification for this point of view should come from a Kohler plot:
A plot of the ratio of the rho(T,B)/rho(T,B=0) versus B/rho(T,B=0) should be independent of temperature.

In the specific materials there will be further complications associated with spatial anisotropy, unequal and temperature dependent election and hole densities, tilted Weyl cones, chiral anomalies, .... However, the essential physics should be the same.

XMR is due to simple (boring old) physics: extremely large mobilities at low temperatures are due to very clean samples and in some cases, near perfect compensation of electron and hole densities.

Postscript. The claim in this post was subsequently shown to be correct.