Condensed concepts

When do revolutions happen? What are the necessary conditions? Here are the claims of two influential political theorists. ``a single spark can cause a prairie fire’’ Mao Tse Tung  “it is not always when things are going from bad to worse that revolutions break out,... On the contrary, it often happens that when a people that have put up with an oppressive rule over a long period without protest suddenly finds the government relaxing its pressure, it takes up arms against it. … liberalization is the most difficult of political arts” Alexis de Tocqueville (1856) Is it possible to test such claims? What is the relative importance of levels of perceived hardship and government illegitimacy, oppression, penalties for rebellion, police surveillance, ...? An important paper in 2002 addressed these issues. Modeling civil violence: An agent-based computational approach  Joshua M. Epstein The associated simulation is available in NetLogo . It exhibits a number of phenomena that

I just realised that last month I had been blogging for ten years. On the five year anniversary, I reflected on the influence that the blog has had on me. I don't have much to add to those reflections. The second five years has not been as prolific but has been just as enriching and I am grateful for all the positive feedback and encouragement I have received from readers.

Individuals have many preferences. One is that we tend to like to associate with people who have some commonality with us. The commonality could involve hobbies, political views, language, age, wealth, ethnicity, religion, values, ... But some of us also enjoy a certain amount of diversity, at least in certain areas of life. We also have varying amounts of tolerance for difference. A common social phenomenon is segregation: groups of people clump together in spatial regions (or internet connectivity) with those similar to them. Examples range from ethnic ghettos and teenage cliques to " echo chambers " on the internet. The figure below shows ethnic/racial segregation in New York City. It is taken from here. In 1971 Thomas Schelling published a landmark paper in the social sciences. It surprised many because it showed how small individual preferences for similarity can lead to large scale segregation . The motivation for his work was to understand how racially segre

Paul Romer won the Nobel Prize in Economics in 2018. There is an interesting podcast where he is in conversation with Tyler Cowan . In it, there is the following quote that readers may love! We subsidize graduate education through money that goes to professors, but we let the professors make the decisions about the problems they work on, and then, therefore, the things the students are trained in. I’d rather let the students be the ones who decide, “Yeah, I don’t really want to work in high-energy physics. It’s kind of dead end. I think there’s something much more exciting in condensed-matter physics.” I mostly post this for amusement. [I thank my economist son, for bringing it to my attention]. However, Romer does raise an interesting issue. There is a distinct contrast between the systems in the USA and Australia. In the USA faculty get grants and use them to hire graduate students. In Australia, most Ph.D. students get their own scholarship (fellowship) which pays their tuitio

There is a very nice paper Complete Set of Elastic Moduli of a Spin-Crossover Solid: Spin-State Dependence and Mechanical Actuation  Mirko Mikolasek, Maria D. Manrique-Juarez, Helena J. Shepherd, Karl Ridier, Sylvain Rat, Victoria Shalabaeva, Alin-Ciprian Bas, Ines E. Collings, Fabrice Mathieu, Jean Cacheux, Thierry Leichle, Liviu Nicu, William Nicolazzi, Lionel Salmon, Gábor Molnár, and Azzedine Bousseksou It investigates the spin-crossover in a specific compound with a suite of techniques, including x-ray diffraction, inelastic neutron scattering, and micro-electromechanical systems (MEMS). The nice results reflect significant advances over the past few decades in neutron scattering and microfabrication. 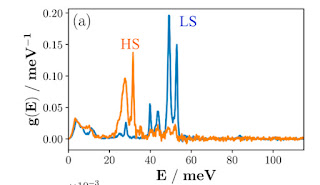The graph below shows the vibrational density of states of the Fe nuclei and the low-spin (LS) and high-spin (HS) states. Note how the LS modes around 50 meV (400 cm-1) soften significantly in the HS state. These modes are the Fe-N stretches in the octahedron. This softening

How would you answer this question if you were asked by a non-expert who likes to learn and understand new things? For example, a smart high school student, your uncle who reads a lot of popular science, an academic colleague in sociology, an economics graduate, ... A draft of my answer is here. I welcome suggestions for improvements. Feel free to try it out on people you know who might be interested.

The physics arXiv started way back in 1991. Yet chemists strongly resisted following suit. Indeed if you posted a preprint on the arXiv American Chemical Society (ACS) journals would not publish it. Eight years ago, Derek Lowe, asked Why Isn't There an arXiv for chemistry? Well, finally ACS has succumbed and set up their own chemrxiv and announced that they will consider manuscripts that have been posted on the arXiv. I thank Ben Powell for letting me know about the promising development.