Deconstructing protein phase diagrams

In the process of coming up with new exam questions for my undergraduate thermodynamics and condensed matter course I came across the following pressure-temperature phase diagram for the protein ribonuclease A at pH 2.0.

It is taken from a 1995 Biochemistry paper and I came across it in the wonderful text by Dill and Bromberg.
[Aside: I wondered if the water freezing was an issue but all along the curve the solvent water is liquid because dP/dT is negative for the liquid-solid line of pure water].

Natural scientific questions are:

• What are the mechanisms of "cold" and pressure-induced denaturation? 
• What are the associated changes in protein structure?
• Is this a generic type of phase diagram for proteins?
• What role does water and hydrophobic interactions play?

A nice review article from 2002 by Smeller discusses how these diagrams are indeed generic and their shape can be understood in terms of a simple thermodynamic theory due to Hawley in 1971.
One simply expands the Gibbs free energy change to second order in T and P relative to some reference pressure P0 and temperature T0,

The pressure induced denaturation can then lead to a volume contraction. This is explained in microscopic terms in a 1998 PNAS paper by Hummer et al.,

The pressure dependence of hydrophobic interactions is consistent with the observed pressure denaturation of proteins

which shows
Pressure-denatured proteins, unlike heat-denatured proteins, retain a compact structure with water molecules penetrating their core. 

When science "managers" put the cart before the horse

This week I read a nice Opinion piece in Physics World, Making an Impact in Biology by Robert Endres. It is worth reading for an update on the contributions that physicists are starting to make to biology. However, one paragraph stood out to me. I found it a bit sad, but not totally surprising:

.... bigger is not always better. When I did research at the Oak Ridge National Laboratory in the US a few years ago, managers used to say that supercomputers should be used in the upcoming field of biology-inspired research, as this would, in retrospect, justify the lab’s investment in a huge computing infrastructure. But they also worried that someone would get “lucky” and find a smaller, more tractable, model or a more efficient algorithm to solve the same problem on a laptop – making the lab’s investment into such projects superfluous. 

Moving to Princeton University shortly afterwards, I realized that these worries were well founded.Top researchers, by asking the right questions and using clever models, could produce high-impact research results without ever needing supercomputers. 

Endres stresses (as I would) that supercomputers have a role in research but should be just  viewed as a possible tool towards for scientific understanding, hopefully the weapon of last resort... They are just a means to an end. Furthermore, funding and politics must never determine scientific strategy.

The cartoon is courtesy of Bob Laughlin.

Long live Fermi liquid theory!

Two important signatures of a Fermi liquid metal are that at low temperatures (i.e. much less than the Fermi temperature) the specific heat is proportional to temperature and the magnetic susceptibility is independent of temperature. Both are proportional to the density of states at the Fermi energy and one can form a dimensionless ratio, the Sommerfeld-Wilson ratio:

R is unity for a non-interacting gas of fermions and is 2 for the impurity contribution in the single impurity Kondo model [Yamada proposed this highly non-trivial result and Wilson confirmed it with the numerical renormalization group].

An important property of heavy fermion metals both the specific heat and susceptibility are enhanced by approximately the same amount. This can be seen in the plot below, where the solid line corresponds to a Wilson ratio of unity.

The plot was first made in Barbara Jones 1985 Cornell Ph.D thesis. 

This version is from Piers Coleman's review article Heavy Fermions: Electrons at the edge of Magnetism.

More than 10 years ago I wrote a paper Wilson's ratio and the spin splitting of magnetic oscillations in quasi-two dimensional metals.
I failed to get it published because of subtle issues about vertex corrections. Nevertheless, the preprint still seems to be of some use to people. See for example, the recent preprint Direct observation of multiple spin zeroes in the underdoped high temperature superconductor YBa2Cu3O6+x

The first 100 days of your postdoc

A standard by which US presidents are judged is by what they achieve in their first 100 days. The benchmark is the first hundred days of FDRs presidency where he began the New Deal.
I believe I once overheard Piers Coleman say that he thought new postdocs should produce a paper in their first 100 days in order to gain momentum and to position themselves for their next job.
This seemed a little extreme to me and almost impossible for many projects. But perhaps that is the point! You should not embark on ambitious projects (especially developing complex new software and building new equipment).

I aim for my postdocs to have submitted a first author paper within 6 months of starting. Most have and I think this has helped build confidence and momentum.

Graphics in LaTeX

In case it is of use to anyone I post this.
I have been occasionally struggling with the inclusion of graphics when running pdfLaTeX on my Mac. Partly this arises from having collaborators who are using PCs and different interfaces for LaTeX.
I found this page following solved my problems.

Emergence of mistakes

The review article that Ben Powell and I just finished,
Quantum frustration in organic Mott insulators: from spin liquids to unconventional superconductors, has just appeared online in Reports on Progress in Physics.

Unfortunately, Figure 1 was incorrectly produced. [We corrected it in the proofs stage and it appears the copy editor did not follow our instructions]. The correct version is below

The Superconducting dance

This cool video was produced by I2CAM as part of the Emergent Universe online science museum.

Quantum dynamics of excited states of Phytochromes: an important class of protein chromophore

I have been learning a little more about phytochromes which are a important class of photo-active biomolecules.  This was stimulated by my previous post about single molecule spectroscopy studies of a photosynthetic protein containing phytochromes. 

I mention here two recent PNAS papers that I found particularly interesting. I just include some key text and figures from the papers.

Ultrafast excited-state isomerization in phytochrome revealed by femtosecond stimulated Raman spectroscopy

Photochemical interconversion between the red-absorbing (P_r) and the far-red-absorbing (P_fr) forms of the photosensory protein phytochrome initiates signal transduction in bacteria and higher plants. The P_r-to-P_frtransition commences with a rapid Z-to-E photoisomerization at the C₁₅C₁₆ methine bridge of the bilin.

This paper reports evidence that this isomerization occurs on the excited state potential energy surface.

Distinct classes of red/far-red photochemistry within the phytochrome superfamily

Phytobilin chromophores can underdo two further possible rotations of the end rings following absorption of red light. Different proteins favour different rotations of these D rings.

The associated quantum chemistry has been considered in Deciphering Intrinsic Deactivation/Isomerization Routes in a Phytochrome Chromophore Model

Ranking Landau

I have decided I should start incorporating a little more history and biographies into my lectures. It is important that students learn something about the "giants" who have paved the way for us.
Since I just taught about "Landau levels" I had a one power point slide biography of Landau. Here is my ranking, for both originality and impact, of Landau's major achievements:

1.  Theory of continuous phase transitions 
2.  Fermi liquid theory
3.  Ginzburg-Landau theory of superconductivity
4.  Theory of superfluidity
5.  The Course in Theoretical Physics

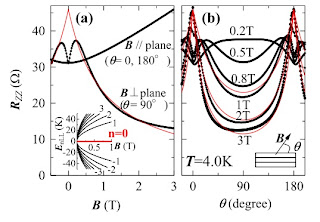
I don't think Landau levels or Landau damping was on the scale as the above achievements. Other people would have worked these out fairly soon if he had not. The main thing that was impressive about "Landau levels" was that he did it when he was 22! and that he sort of "predicted" de Haas van Alphen oscillations in the same year they were observed.

1. has proven to be incredibly important not just in providing a unifying framework for condensed matter but also for broken symmetry in particle physics. It also led to the renormalisation group.

2. is the basis for understanding not just elemental metals but also nuclear physics. Furthermore, it showed the power of using quantum field theoretical techniques based on Green's functions to understand quantum many-body physics.

In preparing I learnt that Landau kept a list ranking system of other theoretical physicists. According to Wikipedia:

Landau kept a list of names of physicists which he ranked on a logarithmic scale of productivity ranging from 0 to 5. The highest ranking, 0.5, was assigned to Albert Einstein. A rank of 1 was awarded to "historical giants" Isaac Newton, Satyendra Nath Bose, Eugene Wigner, and the founding fathers of quantum mechanics, Niels Bohr, Werner Heisenberg, Paul Dirac and Erwin Schrödinger. Landau ranked himself as a 2.5 but later promoted himself to a 2. David Mermin, writing about Landau, referred to the scale, and ranked himself in the fourth division, in the article My Life with Landau: Homage of a 4.5 to a 2.

I must say I think Landau was being modest. Due to the significance of 1. and 2. above, I would rank Landau above Bose, Wigner, and Bohr. As I have blogged before as much as Bohr advanced our understanding of quantum theory I think he also retarded it in several respects.

                   Bohr and Landau in Moscow in 1961
How would you rank these "greats" and Landau's achievements?

Postscript. 2 October 2020. I recently learned that at Landau's 50th birthday party, his colleagues gave him two stone tablets engraved with Landau's "ten commandments", based on his ten most important papers.

Density matrix (1927); Landau diamagnetism (1930); dynamics of ferromagnets (1935, written with Evgenii Lifshitz); theory of phase transitions (1937); intermediate state of superconductors (1937); statistical theory of nuclei (1937); theory of superfluidity (1941); renormalization of electron charge in quantum electrodynamics (1954, with Alexei Abrikosov and Isaac Khalatnikov); theory of Fermi Liquid (1956); and two-component neutrino theory (1957).

Seeing the light from a single biomolecule

Single molecule spectroscopy has opened up a whole new vista on the photophysics and photochemistry of proteins whose functionality depends on optically active chromophores. A Nature Chemistry paper by Goldsmith and Moerner reports their study of the allophycocyanin (APC) protein in solution. It consists of a trimer, each of which contains two phycocyanonobilin (PCB) chromophores (shown in red below). There is a strong excitonic (Forster) coupling within each pair.

I found this particularly interesting because this is a symmetric methine dye, similar to those studied in this recent J. Chem. Phys. paper by Seth Olsen and I.

They observe significant fluctuations in the radiative lifetimes of the chromophore, arguing that this is due to changes in the local environment due to conformational change of the protein. They suggest there are four relevant electronic states.

The results can be compared to A Microscopic Model for the Fluctuations of Local Field and Spontaneous Emission of Single Molecules in Disordered Media

I thank Seth Olsen for bringing the paper to my attention.

Goldilocks on superconductivity

Manifesto for a higher Tc by Dimitri Basov and Andrey Chubukov is an interesting Perspective in Nature Physics. It contains a nice comparison of the new "iron pnictide" superconductors with the cuprates.

They identify three key questions:

(1) Do all high-Tc materials superconduct for the same reason? 

(2) Are the rather anomalous normal-state properties of exotic superconductors a necessary prerequisite for high-Tc superconductivity? 

(3) Is there a generic route to increase Tc? 

They claim that the answer to (1) is yes, exchange of spin fluctuations associated with nesting of different parts of the Fermi surfaces. I am not sure if the majority of people would agree with them on this point.

A few things the Basov and Chubukov also highlight

• The reduction of the kinetic energy by strong correlations deduced from the optical conductivity is a convenient way to characterise the strength of interactions. They claim a 50-70% reduction is optimum for a high Tc. There is a balance ["just right" as found by Goldilocks!]. Stronger interactions increase the pairing interaction but also decrease the mobility of the Cooper pairs.
• The connection between the superfluid density and the loss of low energy spectral weight in the optical conductivity. [Strong dissipation reflected in the Homes scaling where the superfluid density is proportional to the product of Tc and the intralayer dc conductivity.]

In passing, I note that the reduction of the kinetic energy has been measured and discussed for a family of superconducting organic charge transfer salts in this PRL. [Although for idiosyncratic historical/experimental reasons it is plotted as the effective number of charge carriers].

I thank Ben Powell for bringing the paper to my attention.

Visualising Landau level filling and the IQHE

Today I gave a lecture on quantum magnetic oscillations (de Haas van Alphen effect) and determination of the Fermi surface. I struggled to find a simple explanation of how Landau levels lead to oscillations periodic in 1/B.
I briefly mentioned the Quantum Hall Effect. In preparing the lecture I found a nice simulation on Wikipedia which shows how as the magnetic field B increases the Landau level filling varies and this is associated with transitions between Landau level plateaus.

Feynman dreams of a final theory

In 1957 Reviews of Modern Physics published a conference talk by Feynman, Superfluidity and Superconductivity. The last paragraph is fascinating where he laments the problem of finding a theory of superconductivity.
[Click to make it larger]

This highlights just how brilliant BCS were!
Coincidentally, BCS published their theory the same year.

Gell-Mann and Feynman in 1957 

An alternative method of lecture preparation

Normally when I prepare a lecture I tend to follow the strategy:
1. Read the textbook.
2. If need be look at other books.
3.  Write a summary of the relevant part of the book.
4. Work this into a lecture.

Today I followed a different procedure.
1. Don't look at any books.
2. From memory, write out rough notes with the key ideas,  equations, and graphs that I want to communicate.
3. Look at the text to just check and polish details.
4. Rework the rough notes into "neat" notes for the lecture.

The end result was this lecture on Transport properties of metals in the Bloch model.

I think the advantage of this different approach is that it helps prevent one getting bogged down in details that are tangential to the essential points. This might be good for students because it may make the main points clearer. It is also good for me because it saves all the time I sometimes spend struggling through these minor details and worrying about whether or not to include them in the lecture.

I also found that the actual lecture flowed better because more of it was "in my head" rather than stuck in the notes. However, ultimately students should be the judge.

I welcome thoughts on this and on alternative strategies.

Introduction to condensed matter lecture

Tomorrow for PHYS2020 Thermodynamics and Condensed Matter Physics I will give a lecture on Phase diagrams.
Hopefully, students will learn that, contrary to what they were taught in high school, there are many phases of matter, not just solid, liquid, and gas!
Furthermore, they begin to see how the Gibbs free energy is the key quantity which defines the relative stability of different phases (at fixed temperature and pressure).
The video demonstrations I use are from the Video Encyclopedia of Physics Demonstrations.

Economists consider the price of transparency

Previously I posted about how the movie The Inside Job chronicles how conflicts of interest raise questions about the objectivity of some academic economists. Yesterday, I was interested to read in the Princeton Alumni Weekly an interview with Gerald Epstein (an economist at U. Mass.) who

circulated a petition — signed by about 300 economists — calling on the American Economic Association (AEA) to establish a code of conduct requiring that economists who work on the side for financial firms disclose these potential conflicts of interest. That follows a study he and a graduate student completed last year showing that some high-profile economists don’t reveal that they’re paid by financial firms when commenting in academic literature, government testimony, and the media. 

The Chronicle of Higher Education also has an informative article about the petition, the resulting AEA committee, and some of the past history.....

Thermochemistry: heat and light

Today I am giving a lecture to a second year undergraduate physics class on "Thermochemistry and the Third law". A few highlights and questions are:

• A key idea is that of reference states. All thermodynamic state functions (entropy, internal energy, ...)  must be defined relative to some reference.
• The path independence of changes in thermodynamic state functions means that one can calculate changes (e.g., in the enthalpy) via intermediate reactions.
• The third law allows definition of a convenient reference state (T=0).
• Is there a clear way to understand and explain that the "heat of reaction" is the enthalpy change? I still find this a bit confusing. [But pages 33 and 34 of Schroeder's Introduction to Thermal Physics has a helpful discussion].

But, the coolest part of the lecture is the explosions! After all, isn't that is what chemistry is all about? I have some great Chemistry Comes Alive videos of different chemical reactions. Watch the Nitrogen Tri-iodide reaction (detonation)!

Periodic table of Fermi surfaces

At the University of Florida, there is a really nice site which shows the calculated Fermi surfaces of all the metallic elements. The picture above is the Fermi surface of Scandium. Different colours correspond to different bands. In this case, I suspect yellow and purple, also represent electron and hole Fermi surfaces, respectively.

There is a cool poster which shows a periodic table with a picture of each Fermi surface.

Double-barrel questions backfire

I would be curious what other people think about this.
We have all heard it [or done it] before in a seminar.
"I have three questions. The first is, ..[long and technical].... The second is, . [longer..].. The third is..."
I think in seminars audience members should ask only one question at a time. I think it is hard for the speaker to keep track of the questions and answer them all in a coherent and succinct manner.
It is a good discipline for us to try and focus our questions down to one key issue and to try and ask ones that will be helpful to most people present.

Dirac cones produces negative interlayer magnetoresistance

As I have posted before there are quite a few strongly correlated electron materials which exhibit a non-classical interlayer magnetoresistance. Specifically, it has dependence on the field direction which is the opposite to that expected from simple Lorentz force arguments.

This week I read a really nice paper Negative Interlayer Magnetoresistance and Zero-Mode Landau Level in Multilayer Dirac Electron Systems by Toshihito Osada.

The main result is the following expression for the interlayer conductivity in a tilted magnetic field.

A PRL makes an impressive comparison of the theory to experiments on an organic charge transfer salt.

Construction of diabatic states

Much of quantum many-body physics is about constructing effective Hamiltonians. This means substantially reducing the size of the Hilbert space of the system. In quantum chemistry significant insight can be obtained by constructing a few interacting diabatic states. 
How does one do this in practice, particularly if one starts with the results of some high level quantum chemistry calculation? Last week Seth Olsen gave a nice cake meeting talk about a method due to Cederbaum, Schirmer and Meyer.

Basically, one wants to block diagonalise the Hamiltonian and then focus on just one of the blocks which defines the effective Hamiltonian. But there an infinite number of ways of doing this. What criteria does one use to decide that a specific block diagonalisation is the "best one"?

The key mathematical results are in this paper. I give a brief summary of a few of the key things I learnt from Seth's talk.
The central result of the paper is

 [Click on the text to see a larger version]
The key to getting this result is using a theorem which says that if one has a non-singular matrix M then the closest unitary matrix to M is M(M^dagger M)^-{1/2}. This related to matrix polar decomposition and is just the matrix analogue of the fact that for a vector v the closest unit vector to v is a normalised vector parallel to v.

Another way of looking at T is that S diagonalises H and one follows this with the inverse of a block diagonalisation to give the transformation U=S(S_BD)^-1. The matrix T is the closest unitary transformation to T.

A key consequence of practical significance is:

This is particularly useful with State-Averaged Complete Active Space -Self Consistent Field (SA-CAS-SCF) calculations. Then one has very accurate eigenvectors for the few quantum states that one performed the state averaging over.

 For a concrete implementation of all this for a specific molecule see  A diabatic three-state representation of photoisomerization in the green fluorescent protein chromophore

One curious historical aside: a similar approach was considered more than 50 years ago  by Jacques des Cloizeaux (of Bethe ansatz fame) in a paper in the journal Nuclear Physics. 

Compassionate failure

There is a review in the New York Times of the book In the Basement of the Ivory Tower that is worth reading. The book is a memoir of a part-time non-tenured faculty member at a community college in the USA. It argues not every American child is cut out for a college education. It makes the case, on compassionate grounds, that admitting fewer students and failing more is actually the best thing for the students themselves.
On a somewhat related theme see my earlier post Want to improve student learning? Then fail more students!

What is a crystal?

You would have thought such a basic question would have been settled a very long time ago. Solid state physics textbooks written before 1980 certainly give that impression. But no, as recently as 1991, the International Union of Crystallography revised its definition.

After undergraduates learn about crystal structures it is good to teach them about Quasi-crystals. Several good reasons are:

• they are beautiful and fun
• it is a story which should encourage students to question conventional wisdom and not just believe everything in the textbook or that their lecturers tell them
• it illustrates the simple (but sometimes overlooked) truth that just because property A implies property B the converse does not necessarily apply

Here are the slides for my lecture.

The most useful website I found was Introduction to Quasicrystals produced by Steffen Weber. It includes software for producing different tiling patterns and making fourier transforms.

An aside: there is also an interesting 2007 article in Science by Peter Lu and Paul Steinhardt, Decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture. The article generated some "lively" correspondence which you can read online.

I welcome suggestions of other online resources.

How long will it take?

At yesterday's UQ Chemistry seminar Paul Mulvaney underscored the importance of the following law in scientific research.

Hofstadter's Law: It always takes longer than you expect, even when you take into account Hofstadter's Law.

– Douglas Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid

However, in todays UQ Quantum Science seminar we heard an apparent violation of Hofstadter's law! John Teufel said that successful fabrication of the micro opto-mechanical resonator featured in a recent Nature paper took less time than he expected. Indeed the first device he made worked!

It is not over until the fat lady sings

There is a nice informative article Iron superconductivity weathers another storm by Igor Mazin, which just appeared as a Trends piece in the overview journal Physics. It provided me with a nice succinct update on the very fast moving developments in the recently discovered iron-pnictide based superconductors. It seems everything is not as simple as originally thought. As is often the case it is the discovery of new materials which are leading the way and jolting us theorists.
Mazin describes the discovery of three classes of materials. The second two classes present problems for the picture that was developed for the first class.

I. The original Fe pnictide materials [e.g. La(O_1-xF_x)FeAs]  with the key features

•  the electronic band structure is semimetallic, consisting of hole and electron Fermi surface pockets, separated by a (π,π) wave vector in momentum space. 
• a spin excitation with the same wave vector.
•  this spin excitation is the pairing agent for superconductivity 
•  the superconducting order parameters for the holes and for the electrons have opposite signs, with the overall angular momentum being L=0 (s-type); hence the name s_±. 

This means there are no nodes in the superconducting energy gap. This is implicitly a weakly correlated electron picture.

II.   Compounds, KFe₂As₂ , LaFePO, and BaFe₂As₂
These exhibited clear signs of a superconducting energy gap with nodes, inconsistent with class I and the picture above. Furthermore, calculations which claim to produce nodes for these materials also produce them in class I.


III. K_0.8Fe₂Se₂ 
Discovered just last November, this material has only electron Fermi surfaces and so one would expect d-wave pairing [and thus nodes] arising from nesting between the electron Fermi surface pockets.  But  experiments show that there are no nodes in the superconducting energy gap.


With regard to III. Mazin also recounts some experiments which show co-existence of antiferromagnetism and superconductivity [but do they co-exist on the microscopic scale] and uncertainty about stoichiometry and vacancy ordering in different samples.


The figure above is taken from a 2009 Physics Viewpoint, Are iron pnictides the new cuprates?  by Zlatko Tesanovic.

Aside: With regard to the title of this post, Wikipedia gives an interesting history of this colloquialism. I got idea of using the title from Phil Anderson, who used it for a talk in a session on the History of Superconductivity at an APS March Meeting, sometime in the nineties. I think he emphasized that BCS was not the end of the story because the question of gauge invariance, spontaneously broken symmetry, the Josephson effect, anomalous isotope effects, Rowell's tunneling spectra showing the electron-phonon glue, and strong coupling deviations from BCS all needed to be resolved/discovered.

The essence of the nuclear many-body problem

I quite like reading obituaries of scientists because one can actually learn some interesting science and sometimes learn something about how great scientists work.
The November 2010 issue of Physics Today has an obituary for Aage Bohr. [My issue just arrived in the snail mail.] He was the fourth son of Niels Bohr and received the Nobel Prize in 1975 for work in nuclear theory. The obituary gives a beautifully succinct summary of the nuclear many-body problem:

 it had been convincingly demonstrated in the late 1940s that a range of atomic nuclei has properties such as binding energies and electric and magnetic moments that reflect independent-particle motion with a long mean free path of the nucleons in their mean field. This discovery came as a shocking surprise and a dilemma since it implied a shell structure for the nucleus with an analogy to the electronic shell structure for the atom. In contrast, the basis for interpreting the growing body of experimental evidence had been the liquid-drop and compound nucleus models, in which the forces between the nucleons lead to a strong coupling of their motion.

In 1950 a need to reconcile the two contrasting pictures was thus imminent. An important clue was provided by the nuclear electric quadrupole moments, which are sometimes more than an order of magnitude larger than can be attributed to a single proton and directly point to a deformation of the nucleus as a whole. The crucial recognition, also realized by Rainwater, was that the degeneracies of the spherical shell structure may in fact lead to an equilibrium with an anisotropic intrinsic single-particle density and mean field, for nuclei with particles in partially filled shells. A deformation in space suggests the possibility of collective rotation. The striking discovery in the Coulomb excitation process of such rotational band structure in the excitation spectrum provided an early foothold for the collective elements of the picture (1953).

The moments of inertia of the nuclear rotational states were found to be markedly smaller than the moments for rigid rotation that we expected for uncorrelated single-particle motion, thereby exhibiting correlations (1955). In work with David Pines (1958), it was suggested that the necessary correlations could be related to an energy gap in the quasiparticle excitation spectrum created by a pair binding, as in the Bardeen-Cooper-Schrieffer theory of electronic superconductivity.

It gradually emerged that we were, in fact, exploring a quite novel type of many-body quantal system, distinguished at the time by the unique possibility of detailed observations of individual quantal states and their transitions. That exploration became part of a broad development of quantal many-body concepts appropriate to the description of symmetry in a multitude of dimensions (spin-, isospin-, gauge-, orbital-space). The development ultimately revealed the ubiquity of collective features of the nuclear stuff, ranging from oscillation quanta of the fields in the new dimensions to the static deformations and profoundly significant zero-frequency modes of the fields (Goldstone boson). The dilemma of the contrasting pictures that set the development in motion had provided the possibility of a more comprehensive vision—very much in the spirit of Aage’s attitude to conflicts of any kind.

It is also interesting that the last 30 years of his life, Aage Bohr, shifted his focus to questions concerning the foundations of quantum theory; questions his father had focused on.
With regard to eventually following ones father, I see some parallels in myself. Lately I have become increasing interested in questions in molecular biophysics, including the role of water. My late father, a physical biochemist, spent much of his career working on water and proteins.

[Details of the figure are discussed here].

Some key concepts in many-body physics

The two-site Hubbard model lives on!

This week I read two interesting papers 

Singlet Diradical Character from Experiment (a 2010 J. Phys. Chem. Lett.)

Relationship between Third-Order Nonlinear Optical Properties and Magnetic Interactions in Open-Shell Systems: A New Paradigm for Nonlinear Optics (a 2007 Phys. Rev. Lett.)

One thing that is fascinating about both papers is that essentially they are based on a two-site extended Hubbard model!

Indeed I think that studying and understanding the two-site Hubbard model is the first step in learning some of the key concepts associated with quantum many-body physics in both chemistry and solid state physics. It can be used to illustrate:

• origin of covalent chemical bonding
• splitting of singlet & triplet excited states
• different energy scales for charge and spin excitations.
•  tendency to charge localisation (Mott insulator)
•  formation of local magnetic moments
•  antiferromagnetic exchange spin interactions
•  relation between valence bond and molecular orbital methods
•  Configuration Interaction (CI)
• symmetry is useful for labeling many-body states and diagonalising Hamiltonians
• for widely separated (and/or spatially localised) atomic orbitals, electron-electron interactions become increasingly important.
• Electronic correlation effects (entanglement), neglected by Hartree-Fock, can lead to significant qualitative differences.
• Description of many-body states with second quantisation.

Most of this is discussed in a summer school lecture I gave several years ago.