Following up on my previous post and looking forward to extensive discussions with Nanda Dasgupta, David Hinde, and Gerard Milburn over the next two days. Here are some of the questions we are trying to answer:
What internal nuclear degrees of freedom are the source of decoherence in nuclear scattering?
Excited states? Giant dipole resonance? Particle transfer?
Usually one describes the environmental degrees of freedom in terms of a spectral density. What dependence does this have on frequency and the internuclear separation?
What would be a smoking gun experiment to show the presence of decoherence? We want to show how increasing decoherence washes out quantum interference effects. Mott scattering of identical nuclei may be relevant?
What is the relationship between the decoherence which suppresses quantum tunneling and inelastic processes?
Wednesday, April 29, 2009
Tuesday, April 28, 2009
A new party trick?
Todays lecture went pretty well. There were lots of questions. The students love the video demonstration of ice regelation. They said cutting through the ice with a wire would be neat party trick. I looked on Youtube but the only video I could find was this one. Let me know if you find them a better one.
Here is tomorrows lecture, as it stands.
Here is tomorrows lecture, as it stands.
Monday, April 27, 2009
How I came to love nuclear physics
About 18 months ago Gerard Milburn and Phil Stamp invited me to a small PITP workshop in Vancouver on Quantum Information and Many-body Physics. It was there that I met David Hinde and Nanda Dasgupta from Nuclear Physics at ANU (where I was an undergraduate). The talks given by David and Nanda were about a beautiful series of experiments that measure with incredibly high resolution the energy dependence of the cross section for nuclear fusion of two colliding complex nuclei. For fusion to occur quantum tunneling below the potential energy barrier between the nuclei must occur. This is found to be suppressed compared to what is expected for reasonable nuclear potentials and in a PRL with Gerard and a later theory paper with Alexis Diaz-Torres they suggest this suppression is because of decoherence arising from interaction of the relative motion of the nuclei with the internal degrees of freedom of the nuclei. I had been thinking a lot about quantum tunneling of protons in enzymes and reading the theory of quantum tunneling in the presence of a dissipative environment. What really got my attention was the quality of their data which extended over 8 orders of magnitude of the tunneling probability!
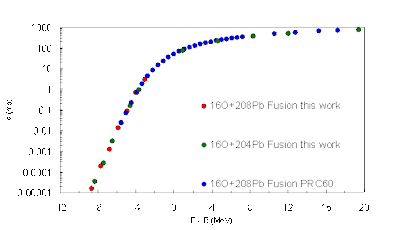
This should provide significant constraints on any theory for tunneling in the presence of decoherence. Nanda will give the physics colloquium at UQ this Friday.

This should provide significant constraints on any theory for tunneling in the presence of decoherence. Nanda will give the physics colloquium at UQ this Friday.
How much of physics is condensed matter physics?
Of the 108 physicists who are most highly cited (ISI Highly Cited.com) for papers published in the period 1981-1999, about 2/3 are condensed matter physicists (26 theorists and 47 experimentalists).
In the past 23 years the Nobel Prize in Physics has been awarded 11 times for work on condensed matter.
In the past 10 years the Nobel Prize in Chemistry has been awarded twice to condensed matter physicists!
In the past 23 years the Nobel Prize in Physics has been awarded 11 times for work on condensed matter.
In the past 10 years the Nobel Prize in Chemistry has been awarded twice to condensed matter physicists!
Some of my favourite phase diagrams
Tomorrow's lecture is on phase diagrams. I like the students to realise that there is a lot more to it than just solid, liquid, and gas. So I show them diagrams like these.
I got that here.

I got that here.
This is the lecture I gave last year. The demo videos (which you can't see, sorry) are from the The Video Encyclopedia of Physics Demostrations, which the students love.

I got that here.

I got that here.
This is the lecture I gave last year. The demo videos (which you can't see, sorry) are from the The Video Encyclopedia of Physics Demostrations, which the students love.
Saturday, April 25, 2009
Am I a psychic or a theoretical physicist?
Although my family does not have a TV we have recently become addicted to watching DVD's of old episodes of The West Wing. This scene from Season 2, Episode 3, got a few laughs.
Friday, April 24, 2009
20 key concepts in thermodynamics and condensed matter
I have just finished revising my lecture for monday 9 a.m. I will mostly review my slant on 11 key ideas from thermodynamics. I will then just flag 9 key ideas that I hope I will be able to teach the students during the next 6 weeks (13 lectures, 4 tutorials). Any feedback is welcome.
Thoughts on the value of teaching from my favourite theoretical chemist
Roald Hoffmann won the Nobel Prize in Chemistry in 1981. He is probably my favourite living theoretical chemist (sorry, Fritz!). Maybe I will write later about why I like his papers so much. But, in the mean time, I draw attention to a nice short article he wrote, Research Strategy: Teach. I am re-reading it this morning to help motivate me, since on monday I start giving a series of lectures on thermodynamics and condensed matter physics to second year undergraduates. Hopefully, I will post some of these and what I am learning in the coming weeks.
Thursday, April 23, 2009
Dimensionless ratios for metals II: Kadowaki-Woods
Following up on my earlier post, one extremely useful ratio is the Kadowaki-Woods ratio, which was originially introducted to understand heavy-fermion compounds. In a Fermi liquid metal, at low temperatures (sometimes as low as a 1 Kelvin) the specific heat capacity is linear in temperature and the resistivity depends quadratically on temperature. (The corresponding co-efficients are denoted gamma and A). Kadowaki and Woods found that for a wide range of heavy fermion compounds the ratio of A to gamma squared was approximately the same. This is important because it was consistent with the idea that the dominant source of scattering (and resistivity) was due to electron-electron scattering and that these materials have a Fermi liquid ground state. Since then it seems whenever people measure a T squared resistivity for a strongly correlated electron material people put the coefficients on the plot, which ends up looking like this: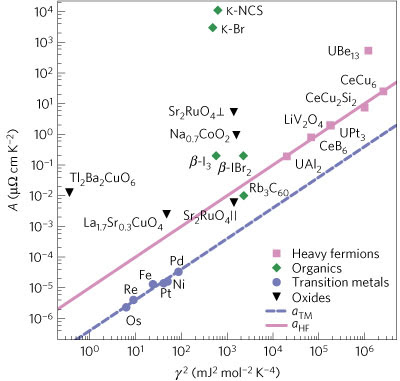
If points do not lie on the line then sometimes it is proposed that the electron-electron scattering is particularly large for the system is non-Fermi liquid. However, more thought is required as to what the real dimensionless ratio is that should be plotted. A paper just published in Nature Physics by my UQ colleagues Anthony Jacko, John Fjaerestad, and Ben Powell provides a definitive answer to this question. They find one needs to take into account the electron density and the spatial dimensionality of the system. The result is the following very impressive plot:

Note how the vertical scale covers resistivities varying by ten orders of magnitude! Hence, the authors have given a universal explaination using Fermi liquid theory for the low temperature resistivity in a diverse range of materials. This is a striking example of universality: where properties of a system are essentially independent of chemical and structural details.
One question I have is what the implications are of this analysis for some claims of non-Fermi liquid behaviour, especially near quantum critical points. For example, deviations from the Kadowaki-Woods ratio were used to characterise the breakup of heavy electrons near a quantum critical point.

If points do not lie on the line then sometimes it is proposed that the electron-electron scattering is particularly large for the system is non-Fermi liquid. However, more thought is required as to what the real dimensionless ratio is that should be plotted. A paper just published in Nature Physics by my UQ colleagues Anthony Jacko, John Fjaerestad, and Ben Powell provides a definitive answer to this question. They find one needs to take into account the electron density and the spatial dimensionality of the system. The result is the following very impressive plot:

Note how the vertical scale covers resistivities varying by ten orders of magnitude! Hence, the authors have given a universal explaination using Fermi liquid theory for the low temperature resistivity in a diverse range of materials. This is a striking example of universality: where properties of a system are essentially independent of chemical and structural details.
One question I have is what the implications are of this analysis for some claims of non-Fermi liquid behaviour, especially near quantum critical points. For example, deviations from the Kadowaki-Woods ratio were used to characterise the breakup of heavy electrons near a quantum critical point.
Wednesday, April 22, 2009
Mind the gap
A particularly striking example of a new quantum state of matter is the pseudogap state found in high-temperature cuprate superconductors. The temperature-doping phase diagram of the cuprates contains a large region between the antiferromagnetic Mott insulator and superconducting phases known as the pseudogap region. Many observed properties are that of a metal in which the density of states is suppressed near the Fermi energy. The pseudogap state is a distinctive feature of the cuprates and understanding its origin and relationship to superconductivity is highly contentious. A nice review by Norman, Pines, and Kallin (based on a workshop in 2004) considers three alternative schematic phase diagrams (temperature T versus doping x) for the cuprate superconductors.

The solid line denotes the superconducting transition temperature Tc and the dashed line the pseudogap temperature T*. A key question is whether T* is a crossover temperature or is actually associated with a phase transition. In (2) there is a quantum phase transition at the hole doping level xc which is close to the value at which the superconducting transition temperature Tc is maximal (i.e., optimal doping).
Proposals for the physical origin of the pseudogap include:
• pre-formed superconducting pairs
• resonating valence bonds (RVB)
• short-range spin correlations
• a new state of matter such as a d-density wave
• long-range antiferromagnetic spin fluctuations due to a magnetic quantum critical point.
It has been established by ARPES (angle-resolved photoemission spectroscopy) that the magnitude of the pseudogap varies over the Fermi surface. The wavevector dependence of the magnitude of the pseudogap has a d-wave character similar to that of the superconducting state. Furthermore, the quasi-particle excitations have a much longer lifetime at wavevectors near where the nodes in the pseudogap occur. Outstanding questions, besides the physical origin of the pseudogap ,include:
• Does the pseudogap temperature T* correspond to an actual phase transition (i.e., a new state of matter)23 or is it just a crossover temperature? If the former is there an order parameter and a broken symmetry associated with the pseudogap state?
• In the absence of superconductivity (e.g., if it is suppressed by a large magnetic field) does T* vanish at a particular doping corresponding to a quantum critical point? If so, is this point responsible for the optimal Tc and/or the non-Fermi liquid properties of the metallic phase at optimal doping?
• Can a pseudogap cause the temperature and frequency dependence of the interlayer and the intralayer conductivity to be distinctly different?
• How ubiquitous is anisotropic pseudogap in strongly correlated electron materials?
Specifically, does it occur in layered organic superconductors, overdoped cuprates, electron doped cuprates, heavy fermion metals, and iron pcinitides?
• Can the pseudogap be closed with a Zeeman magnetic field?
• Is there a change in the topology of the Fermi surface between the left and right sides of the phase diagrams in Figure above (i.e., as one goes from underdoped to overdoped) ?

The solid line denotes the superconducting transition temperature Tc and the dashed line the pseudogap temperature T*. A key question is whether T* is a crossover temperature or is actually associated with a phase transition. In (2) there is a quantum phase transition at the hole doping level xc which is close to the value at which the superconducting transition temperature Tc is maximal (i.e., optimal doping).
Proposals for the physical origin of the pseudogap include:
• pre-formed superconducting pairs
• resonating valence bonds (RVB)
• short-range spin correlations
• a new state of matter such as a d-density wave
• long-range antiferromagnetic spin fluctuations due to a magnetic quantum critical point.
It has been established by ARPES (angle-resolved photoemission spectroscopy) that the magnitude of the pseudogap varies over the Fermi surface. The wavevector dependence of the magnitude of the pseudogap has a d-wave character similar to that of the superconducting state. Furthermore, the quasi-particle excitations have a much longer lifetime at wavevectors near where the nodes in the pseudogap occur. Outstanding questions, besides the physical origin of the pseudogap ,include:
• Does the pseudogap temperature T* correspond to an actual phase transition (i.e., a new state of matter)23 or is it just a crossover temperature? If the former is there an order parameter and a broken symmetry associated with the pseudogap state?
• In the absence of superconductivity (e.g., if it is suppressed by a large magnetic field) does T* vanish at a particular doping corresponding to a quantum critical point? If so, is this point responsible for the optimal Tc and/or the non-Fermi liquid properties of the metallic phase at optimal doping?
• Can a pseudogap cause the temperature and frequency dependence of the interlayer and the intralayer conductivity to be distinctly different?
• How ubiquitous is anisotropic pseudogap in strongly correlated electron materials?
Specifically, does it occur in layered organic superconductors, overdoped cuprates, electron doped cuprates, heavy fermion metals, and iron pcinitides?
• Can the pseudogap be closed with a Zeeman magnetic field?
• Is there a change in the topology of the Fermi surface between the left and right sides of the phase diagrams in Figure above (i.e., as one goes from underdoped to overdoped) ?
Tuesday, April 21, 2009
Career advice from my mentor
I was privileged to do a postdoc with John Wilkins at Ohio State University. I not only learnt a lot about physics from him but also important skills for surviving (and prospering) in research. I still remember him getting a room full of postdocs and graduate students to chant, "17 point type is the smallest! 17 point type is the smallest! " over and over again, after he got sick of us using too small of fonts in our practice talks for the APS March Meeting. Much of Wilkin's advice is distilled in one page guides which are available here. Topics covered include interviewing, giving a terrible talk, writing a Physical Review Letter, getting a grant, ....Some are quite humorous.
Monday, April 20, 2009
Dimensionless ratios for metals
When the quantum theory of metals was formulated in the 1920's and 1930's significant insight was obtained by considering several dimensionless ratios which show that different physical quantities are related to each other purely in terms of fundamental constants. Furthermore, using quantum many-body theory and Landau's Fermi liquid theory it has been possible to show that even in strongly correlated electron materials such as heavy fermion compounds many of these ratios have the same value that they do for a non-interacting fermion gas. This is surprising because some of the quantities can be orders of magnitude larger than for a non-interacting system. Important examples include the Sommerfeld-Wilson ratio (ratio of the magnetic susceptibility to the linear temperature coefficient of the specific heat capacity), Lorentz ratio (associated with the Weidemann-Franz law), Korringa ratio, and the Kadowaki-Woods ratio. These ratios are useful because they
- demonstrate universality
- tell us that the same electrons are reponsible for the two quantities that form the ratio
- provide significant constraints on theories
- can be used as a criteria for non-Fermi liquid theory
Saturday, April 18, 2009
Will blogs revolutionize how science is done?
The latest issue of Nature Physics has an editorial which is worth thinking about. It is followed by a Commentary by Michael Nielsen. Both claim that due to new on-line tools such as blogs and wikis a major revolution is about to occur in the way science is done. Although, I remain to be convinced the changes will be as dramatic, as significant, and as fast as claimed, there are some important points I am in sympathy with.
Indeed this why I started this blog!
* Scientists are too secretive about sharing new ideas and data.
* Science will advance faster the more informal and unstructured collaboration occurs.
* We could all benefit from "picking the brains" of great scientific minds. Blogs, wiki's, etc. provide a highly efficient means of this happening.
* There are significant amounts of insights, experiences, data, questions, that never "see the light of day" because they are not suitable for conventional
publications but need to be disseminated.
Indeed this why I started this blog!
* Scientists are too secretive about sharing new ideas and data.
* Science will advance faster the more informal and unstructured collaboration occurs.
* We could all benefit from "picking the brains" of great scientific minds. Blogs, wiki's, etc. provide a highly efficient means of this happening.
* There are significant amounts of insights, experiences, data, questions, that never "see the light of day" because they are not suitable for conventional
publications but need to be disseminated.
A new twist on why the Incredible Hulk glows green?

The 2008 Nobel Prize in Chemistry was awarded for the discovery and development of Green Flourescent Proteins. An important question is
Why does the chromophore cease to be flourescent when it is in the gas phase or is removed from the protein and dissolved in water?
The most natural (partial) explaination is that inside the protein non-radiative decay channels are quenched. In particular, quantum chemical calculations suggest that in the gas phase the chromophore undergoes rapid photo-isomerization. i.e., when it absorbs a photon and makes a transition into the lowest excited singlet state it twists about the central carbon atom (methine bridge).
Such molecules are strongly correlated electron systems.
Calculating the relevant potential energy surfaces (which determine the excited state quantum dynamics) at a level of approximation that gives qualitatively
reliable results for such a large molecule is at the boundary of what is currently possible in computational chemistry. Furthermore, even if one can do such a calculation is it possible to obtain some chemical and physical insight as to the key issues. I believe that Seth Olsen and I recently made significant progress in this regard. Our paper has been accepted for publication in the Journal of Chemical Physics. The figure below provides a simple picture of the relevant resonating valence bond states relevant to the three lowest singlet states.

Seth will soon be giving seminars on this work at two of the worlds leading groups on computational photochemistry, Mike Robb's group at Imperial College London, and Massimo Olivucci's group in Sienna, Italy. I look forward to hearing their feedback.
Thursday, April 16, 2009
A new era in catalysis research
One of my Ph.D students, Elvis Shoko recently had a very stimulating and productive trip to the U.S.A. I think the value of the trip was significantly enhanced by setting specific goals for each activity and writing a detailed trip report about what he learnt. During the trip he attended a Gordon Research Conference on Chemical Reactions on Surfaces. I thought his summary was very helpful and perceptive:
A brief overview of the field can be constructed from the talks given at the conference. On the experimental side, the trend is to move away from studying the properties of catalysts before and after a chemical reaction to studying them in situ. This provides the opportunity to watch surface reactions in real-time [Science 322, 932 (2008)]. This paradigm shift is matched on the theoretical side by a shift from trying to understand surface reactions from a study of equilibrium structures to real-time studies using techniques from kinetic- and adaptive kinetic Monte Carlo. This follows the realization that dynamic centres are key to catalytic processes [JACS 127, 9267 (2005)]. Another important trend on the experimental side is the nanoscale engineering of catalyst materials. One of the key drivers for the investment in catalyst research in the 21st century is the growing demand for clean energy as detailed in recent reports from the US Department of Energy and the National Academies.
A brief overview of the field can be constructed from the talks given at the conference. On the experimental side, the trend is to move away from studying the properties of catalysts before and after a chemical reaction to studying them in situ. This provides the opportunity to watch surface reactions in real-time [Science 322, 932 (2008)]. This paradigm shift is matched on the theoretical side by a shift from trying to understand surface reactions from a study of equilibrium structures to real-time studies using techniques from kinetic- and adaptive kinetic Monte Carlo. This follows the realization that dynamic centres are key to catalytic processes [JACS 127, 9267 (2005)]. Another important trend on the experimental side is the nanoscale engineering of catalyst materials. One of the key drivers for the investment in catalyst research in the 21st century is the growing demand for clean energy as detailed in recent reports from the US Department of Energy and the National Academies.
What is temperature?
Doug Natelson, writes one of the few blogs on condensed matter physics. He recently wrote a blog on What is temperature? I don't really like his perspective. I think it is best to define temperature in macroscopic and operational terms, using the zeroth law of thermodynamics. The attached slides are from my undergraduate lectures. The key ideas are
* the zeroth law allows us to assign a single number to a thermodynamic system that has the important property that this number will tell us whether or not the system will change when it is brought into thermal contact with another system.
* a thermometer is just a thermodynamic system with just one state variable.
* the zeroth law allows us to assign a single number to a thermodynamic system that has the important property that this number will tell us whether or not the system will change when it is brought into thermal contact with another system.
* a thermometer is just a thermodynamic system with just one state variable.
Wednesday, April 15, 2009
How can we work together well?
A colleague asked me to do a post about avoiding misunderstandings and problems in student-supervisor relationships. One thing I have found extremely helpful and effective is for anyone I supervise (postdocs and students) to write out and discuss a list of expectations. What we expect of each other and of ourselves. One of my Ph.D students, Elvis Shoko, kindly agreed to allow me to post the document he drafted. The idea of "win/win performance agreements" is discussed in Habit 4 of The 7 Habits of highly effective people: restoring the character ethic by Stephen R. Covey.
Smoothing out the quantum noise
David Reilly from Sydney University will be at UQ this friday to give the physics colloquium. Unfortunately, I will be in Sydney but plan on catching up with David on thursday. I knew David when he was a Ph.D student at UNSW. He recently returned to Sydney after a postdoc in Charlie Marcus' group at Harvard. He published a really nice Science paper and Physical Review Letter, characterising how electron spins in double quantum dots are decohered by the fluctuating nuclear spins. A few years back Sam Young Cho and I considered how such double quantum dots could be used for a solid state realisation of Werner states (i.e., quantum states which are entangled but do not violate Bell inequalities). An associated talk which I will give at Sydney University on thursday is here.
what is emergence?
I2CAM is developing a web-based interactive museum about emergent behavior, It is "targeted at Internet savvy individuals, typically college bound/educated 14-30 year olds, this site will introduce non-scientists and scientists alike to the concept of emergence."
Tuesday, April 14, 2009
A great way to start learning (and understanding) quantum physics?
At UQ the Faculty of Science has an Advanced Study Program, which gets gifted (and hopefully highly motivated!) undergraduates involved in research early. I have a second year student, Michael Horn, who is doing a project with me on optically excited states of biomolecules. However, he hasn't taken any courses in quantum physics yet.
So what should he read? Volume III of The Feynman lectures turns out to be ideal. I never cease to be amazed at Feynman's originality and profound insight. He certainly does not treat topics in the conventional order! Just using a Hamiltonian matrix he describes the ammonia maser, the hydrogen molecule, benzene, dyes, the neutral K-meson, semiconductor devices, ... Only after all this in chapter (lecture) 16 does he introduce the Schrodinger equation (i.e., the differential equation) and the hydrogen atom. Michael only needs to read 12 lectures to learn what he needs to know to understand the essential quantum physics associated with a lot of the photochemical properties of organic molecules.
So what should he read? Volume III of The Feynman lectures turns out to be ideal. I never cease to be amazed at Feynman's originality and profound insight. He certainly does not treat topics in the conventional order! Just using a Hamiltonian matrix he describes the ammonia maser, the hydrogen molecule, benzene, dyes, the neutral K-meson, semiconductor devices, ... Only after all this in chapter (lecture) 16 does he introduce the Schrodinger equation (i.e., the differential equation) and the hydrogen atom. Michael only needs to read 12 lectures to learn what he needs to know to understand the essential quantum physics associated with a lot of the photochemical properties of organic molecules.
Quantum dancing monkeys? Valence bond theory of benzene
Hopefully this will be the first of several posts related to valence bond theory. I attach a nice treatment of a simple Heisenberg model for benzene, copied from a book, Electronic Properites of Conjugated Polymers by William Barford. The book also shows how strong electronic correlations lead to a significant different ordering of excited electronic states than predicted by molecular orbital theory and density functional theory based approximations. So what does this have to do with dancing monkeys and quantum entanglement?
Monday, April 13, 2009
Puzzling magnetoresistance
A wide range of new functional electronic materials are layered metals whose electrical resistance changes significantly in the presence of a magnetic field. One example is the giant magnetoresistance (GMR) materials, recognized in the 2007 Nobel Prize in Physics. Many of the latest memories in computers and iPods are based on GMR materials.
In semi-classical transport theory for conventional metals magnetoresistance arises from the Lorentz force (F=vxB) on the electrons. This force is zero when the magnetic field and current are parallel and maximal when the field and current are perpendicular. However, in a structurally and chemically diverse range of layered metals there is a large magnetoresistance when the magnetic field and current are parallel, both being perpendicular to the layers. In contrast, the interlayer magnetoresistance is small when the field is parallel to the layers. This unusual angular dependence of the magnetoresistance has been observed in several organic charge transfer salts, intercalated graphite, ruthenates, and semiconductor superlattices.
These slides show examples of the strange angle-dependent magnetoresistance for these materials.
What is the origin of this non-classical magnetoresistance?
I have been working on this for several years. It is a hard problem, which appears to be related to the problem of magic angles in magnetoresistance in organic metals. This paper discusses in more detail some of the issues.
I welcome new ideas.
In semi-classical transport theory for conventional metals magnetoresistance arises from the Lorentz force (F=vxB) on the electrons. This force is zero when the magnetic field and current are parallel and maximal when the field and current are perpendicular. However, in a structurally and chemically diverse range of layered metals there is a large magnetoresistance when the magnetic field and current are parallel, both being perpendicular to the layers. In contrast, the interlayer magnetoresistance is small when the field is parallel to the layers. This unusual angular dependence of the magnetoresistance has been observed in several organic charge transfer salts, intercalated graphite, ruthenates, and semiconductor superlattices.
These slides show examples of the strange angle-dependent magnetoresistance for these materials.
What is the origin of this non-classical magnetoresistance?
I have been working on this for several years. It is a hard problem, which appears to be related to the problem of magic angles in magnetoresistance in organic metals. This paper discusses in more detail some of the issues.
I welcome new ideas.
Thursday, April 9, 2009
Think twice before you send that email (or post on your blog!)
An article last year in the Career section of The Australian newspaper is worth reading and digesting. I posted it outside my office door for a while.
It is safest to assume that any email you send may be forwarded (possibly by mistake) to someone else. Young scientists (Ph.D students, postdocs, and faculty without tenure) should be particularly wary. Even if an email is not intentionally forwarded it may be printed and left at a public printer. It is also amusing (or distressing) to sometimes be forwarded emails which appear to be innocuous but which if one scrolls down one finds "interesting" comments about colleagues.
Also, never try to solve relational problems via email. Sometimes it is best to use the "sneakernet" and walk down the corridor or pick up the phone.
It is safest to assume that any email you send may be forwarded (possibly by mistake) to someone else. Young scientists (Ph.D students, postdocs, and faculty without tenure) should be particularly wary. Even if an email is not intentionally forwarded it may be printed and left at a public printer. It is also amusing (or distressing) to sometimes be forwarded emails which appear to be innocuous but which if one scrolls down one finds "interesting" comments about colleagues.
Also, never try to solve relational problems via email. Sometimes it is best to use the "sneakernet" and walk down the corridor or pick up the phone.
Thursday, April 2, 2009
Survival of the fittest quantum noise?
A series of recent theoretical papers from groups at Harvard and Imperial college have raised the possibility that biological systems may use the sensitivity of quantum systems to noise to optimise energy transport.
(I thank Drew Ringsmuth and Gerard Milburn for bringing these papers to my attention).
These papers were inspired by experiments at Berkeley which found that in a particular photosynthetic complex at a temperature of 77K (n.b., not room temperature) there was evidence for quantum coherence of excitons for time scales of the order of a few hundred femtoseconds. Furthermore, it was claimed that the protein is actually designed to protect this coherence.
These new theoretical papers perform calculations on several model systems and make the general observation that there is an optimum non-zero coupling to the environment for maximum efficiency and rate of transport. This goes against ones simple intuition that one might think that noise will aways reduce efficiency and rate of energy transfer. This is interesting and I think it is worth pointing out a much simpler (and older) example that illustrates this principle: a classic result of Marcus-Hush electron transport theory.
Following Weiss’ (useful, encyclopedic, but unfortunately opaque)
book on Quantum Dissipative Systems (see especially Section 20.1) this observation can be framed in the following terms: consider a spin boson model with bias epsilon and coupling matrix element Delta between two quantum states, denoted 1 and 2.
The reorganisation energy lambda is a measure of the strength of the coupling of the environment to the two quantum states. At temperatures larger than Delta and the characteristic frequency of the boson (environment) bath and for Delta small enough that the “non-adiabatic” limit holds. The rate of transfer from state 1 to state 2 is given by equation (5) in Marcus’ Nobel lecture.
The rate is a maximum when the reorganisation energy equals the bias. See Figures 7 and 8 in Marcus’ Nobel lecture. Hence, for a fixed bias epsilon there is an optimal (non-zero) value for the coupling to the environment.
Thus, this is another example of how the optimum rate occurs for a non-zero coupling to the environment.
Although Marcus and Hush were concerned with electron transfer, Joel Gilmore and I showed the mathematics is identical for Forster resonant energy transfer between chromophores.
Have biomolecules evolved to optimise energy transfer, as claimed by some? I doubt it.
A recent article claims that for electron transfer in proteins it appears that the reorganisation energy is NOT particularly selected by nature to optimise the rate.
(I thank Drew Ringsmuth and Gerard Milburn for bringing these papers to my attention).
These papers were inspired by experiments at Berkeley which found that in a particular photosynthetic complex at a temperature of 77K (n.b., not room temperature) there was evidence for quantum coherence of excitons for time scales of the order of a few hundred femtoseconds. Furthermore, it was claimed that the protein is actually designed to protect this coherence.
These new theoretical papers perform calculations on several model systems and make the general observation that there is an optimum non-zero coupling to the environment for maximum efficiency and rate of transport. This goes against ones simple intuition that one might think that noise will aways reduce efficiency and rate of energy transfer. This is interesting and I think it is worth pointing out a much simpler (and older) example that illustrates this principle: a classic result of Marcus-Hush electron transport theory.
Following Weiss’ (useful, encyclopedic, but unfortunately opaque)
book on Quantum Dissipative Systems (see especially Section 20.1) this observation can be framed in the following terms: consider a spin boson model with bias epsilon and coupling matrix element Delta between two quantum states, denoted 1 and 2.
The reorganisation energy lambda is a measure of the strength of the coupling of the environment to the two quantum states. At temperatures larger than Delta and the characteristic frequency of the boson (environment) bath and for Delta small enough that the “non-adiabatic” limit holds. The rate of transfer from state 1 to state 2 is given by equation (5) in Marcus’ Nobel lecture.
The rate is a maximum when the reorganisation energy equals the bias. See Figures 7 and 8 in Marcus’ Nobel lecture. Hence, for a fixed bias epsilon there is an optimal (non-zero) value for the coupling to the environment.
Thus, this is another example of how the optimum rate occurs for a non-zero coupling to the environment.
Although Marcus and Hush were concerned with electron transfer, Joel Gilmore and I showed the mathematics is identical for Forster resonant energy transfer between chromophores.
Have biomolecules evolved to optimise energy transfer, as claimed by some? I doubt it.
A recent article claims that for electron transfer in proteins it appears that the reorganisation energy is NOT particularly selected by nature to optimise the rate.
Quantum biology?!?
The role of quantum dynamics in biomolecular function is of great interest to me. Unfortunately, there are some highly speculative ideas and claims being made on this topic.
I had a student, Joel Gilmore, complete a Ph.D thesis on this topic. Some of our results are published in a review article we recently published in the Journal of Physical Chemistry. (My first paper in that journal!) We were able to actually quantify the effect of the environment on quantum dynamics of excited states in optically active biomolecules. This included finding the timescale relevant to the "collapse" of the wavefunction!
I also organised an Exploratory Workshop on this topic for I2CAM.
In my view, some of the key questions in this field are:
When is quantum dynamics (e.g., tunneling, coherence, and entanglement) necessary for functionality?
Do biomolecules exploit dynamics to enhance functionality?
What are the model molecular systems that should be the focus of concerted theoretical and experimental study?
What are the principles for developing nanotechnologies that can be learned from mimicking biomolecular nanoscale devices?
More posts on this topic will be forthcoming.
I had a student, Joel Gilmore, complete a Ph.D thesis on this topic. Some of our results are published in a review article we recently published in the Journal of Physical Chemistry. (My first paper in that journal!) We were able to actually quantify the effect of the environment on quantum dynamics of excited states in optically active biomolecules. This included finding the timescale relevant to the "collapse" of the wavefunction!
I also organised an Exploratory Workshop on this topic for I2CAM.
In my view, some of the key questions in this field are:
When is quantum dynamics (e.g., tunneling, coherence, and entanglement) necessary for functionality?
Do biomolecules exploit dynamics to enhance functionality?
What are the model molecular systems that should be the focus of concerted theoretical and experimental study?
What are the principles for developing nanotechnologies that can be learned from mimicking biomolecular nanoscale devices?
More posts on this topic will be forthcoming.
Wednesday, April 1, 2009
Spray on integrated circuits
MOSFETs are probably the most ubiquitous device in modern electronic circuits.
A major effort is underway to develop commercially viable organic devices that can exploit the ease and low-cost processing associated with polymers.
This week at the weekly science meeting of the Centre for Organic Photonics and Electronics (COPE) we are going to discuss a paper about enhancement of carrier mobilities in organic field effect transistors (OFETs).
From current-voltage (I-V)characteristics the paper extracts mobilities, threshold voltages, and the density of trap states. Since it was not clear to me how one gets such quantities from the data I went on a search and found this widely cited 1998 review by Horowitz. It was helpful because he gives equations which can be used to extract these parameters from I-V characteristics. However, he gives no derivations or references for the derivation and so I am still in the dark about the assumptions and range of validity of the equations. Hopefully, someone will comment on this posting and illuminate it for me. One concern and question I have is: to what extent the equations require a semiconductor band picture for their validity? Or are they just a consequence of electrostatics and the charge accumulation at the organic-insulator interface? After all, sections 3.1 and 3.2 or the article explain why such a picture should not hold in the organic materials used. (This point is not really appreciated enough by people who work in the field).
Other useful and more recent reviews are here and here.
Both reviews stress that charge transport in these materials is still poorly understood.
A major effort is underway to develop commercially viable organic devices that can exploit the ease and low-cost processing associated with polymers.
This week at the weekly science meeting of the Centre for Organic Photonics and Electronics (COPE) we are going to discuss a paper about enhancement of carrier mobilities in organic field effect transistors (OFETs).
From current-voltage (I-V)characteristics the paper extracts mobilities, threshold voltages, and the density of trap states. Since it was not clear to me how one gets such quantities from the data I went on a search and found this widely cited 1998 review by Horowitz. It was helpful because he gives equations which can be used to extract these parameters from I-V characteristics. However, he gives no derivations or references for the derivation and so I am still in the dark about the assumptions and range of validity of the equations. Hopefully, someone will comment on this posting and illuminate it for me. One concern and question I have is: to what extent the equations require a semiconductor band picture for their validity? Or are they just a consequence of electrostatics and the charge accumulation at the organic-insulator interface? After all, sections 3.1 and 3.2 or the article explain why such a picture should not hold in the organic materials used. (This point is not really appreciated enough by people who work in the field).
Other useful and more recent reviews are here and here.
Both reviews stress that charge transport in these materials is still poorly understood.
Subscribe to:
Posts (Atom)
Thermodynamics and emergence
Novelty. Temperature and entropy are emergent properties. Classically, they are defined by the zeroth and second laws of thermodynamics, re...
-
Is it something to do with breakdown of the Born-Oppenheimer approximation? In molecular spectroscopy you occasionally hear this term thro...
-
I welcome discussion on this point. I don't think it is as sensitive or as important a topic as the author order on papers. With rega...
-
Nitrogen fluoride (NF) seems like a very simple molecule and you would think it would very well understood, particularly as it is small enou...

