Experimental observation of the Hund's metal to bad metal crossover

A definitive experimental signature of the crossover from a Fermi liquid metal to a bad metal is the disappearance of a Drude peak in the optical conductivity. In single band systems this occurs in proximity to a Mott insulator and is particularly clearly seen in organic charge transfer salts and is nicely captured by Dynamical Mean-Field Theory (DMFT).

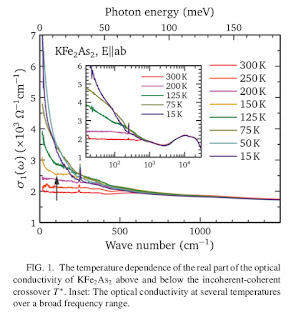
An important question concerning multi-band systems with Hund's rule coupling, such as iron-based superconductors, is whether there is a similar collapse of the Drude peak. This is clearly seen in one material in a recent paper

Observation of an emergent coherent state in the iron-based superconductor KFe2As2 
Run Yang, Zhiping Yin, Yilin Wang, Yaomin Dai, Hu Miao, Bing Xu, Xianggang Qiu, and Christopher C. Homes

Note how as the temperature increases from 15 K to 200 K that the Drude peak collapses. 

The authors give a detailed analysis of the shifts in spectral weight with varying temperature by fitting the optical conductivity (and reflectivity from which it is derived) at each temperature to a model consisting of three Drude peaks and two Lorentzian peaks. Note this involves twelve parameters and so one should always worry about the elephants trunk wiggling.

On the other hand, they do the fit without the third peak, which is of the greatest interest as it is the sharpest and most temperature dependent, and claim it cannot describe the data.

The authors also perform DFT+DMFT calculations of the one-electron spectral function (but not the optical conductivity) and find it does give a coherent-incoherent crossover consistent with the experiment. However, the variation in quasi-particle weight with temperature is relatively small.

Maximise your comparative advantage

A snarky mathematician [Stanislaw Ulam] once challenged the great Paul Samuelson to name an economic proposition that is true but not obvious. Samuelson’s choice was comparative advantage, which shows, among other things, that there are mutual gains from trade even if one nation is better than another at producing everything.  

 Here’s a homespun illustration. Suppose a surgeon is also a whiz at house painting—better than most professional painters. Should she therefore take time off from her medical practice to paint her own house? Certainly not. For while she may have a slight edge over most painters when it comes to painting walls, she has an enormous edge when it comes to performing surgery. Surgery is her comparative advantage, so she should specialize in it and let some others, who don’t know their way around an operating room, specialize in painting—their comparative advantage. That way, the whole economy becomes more efficient.  

 The same principle applies to nations. Even if China could manufacture everything more efficiently than the U.S. can (which it can’t), it would still make sense for the U.S. to specialize in the goods in which it has comparative advantages, and then trade with China for the things it wants but doesn’t produce. Both countries wind up getting more for less.

Alan Blinder
A Brief Introduction to Trade Economics 
Why deficits are normal, especially for a country like the U.S., and what is comparative advantage.

It is worth considering the relevance of the concept of comparative advantage to doing science and its administration.

Individual scientists, should identify their comparative advantage [e.g. a particular technique, a sub-field, approach, instrument, ...] and maximise it. Furthermore, they may be better than their grad students at doing certain things, but that does not mean they should do those things.
Some exceptional scientists may be good at public outreach and chairing committees but they need to be careful such things don't stop them from doing the science for which they have a clear comparative advantage.

Collaborations should also make sure individuals maximise their comparative advantage. A collaboration may also have a particular comparative collective advantage [e.g. combined theory and experiment, chemists and physicists, ...].

Yet, there is significant sociological pressure against maximising comparative advantage for the good of science as a whole. For example, the pressure to publish more papers may lead to a gifted individual focusing on low-lying fruit and publons, rather than maximising their competitive advantage to tackle and solve difficult problems with patience and creativity.
The pressure to work on fashionable topics (e.g. to boost citation indices or get funding) may pressure scientists to leave fields in which they have comparative advantage.

Administrators should think twice before increasing the pressure on scientists to do more of their own administration, lab maintenance, public outreach, IT support, secretarial work, ...
These are not things in which they have a comparative advantage.

Questions about slave-particle mean-field theories of Hund's metals

One of most interesting new ideas about quantum matter from the last decade is that of a Hund's metal. This is a strongly correlated metal that can occurs in a multi-orbital material (model) as a result of the Hund's rule (exchange interaction) J that favours parallel spins in different orbitals.
Above some relatively low temperature (i.e. compared to the bare energy scales such as non-interacting band-widths, J, and Hubbard U) the metal becomes a bad metal, associated with incoherent excitations.
An important question concerns the extent to which slave mean-field theories can capture the stability of the Hund's metal, and its properties including the emergence of a bad metal above some coherence temperature, T*.

In a single-band Hubbard model, the strongly correlated metallic phase that occurs in proximity to a Mott insulator is associated with a small quasi-particle weight and suppression of double occupancy, reflecting suppressed charge fluctuations. This is captured by slave-boson mean-field theory, including the small coherence temperature.

In contrast, to a "Mott metal", a Hund's metal is associated with suppression of singlet spin fluctuations on different orbitals, without suppression of charge fluctuations and is seen in a Z_2 slave-spin mean-field theory at zero temperature.

Specific questions are whether slave mean-field theories at finite temperature can capture the following?

• The coherence temperature, T*.
• A suppression of spin singlet fluctuations at T increases towards T*.
• An orbital-selective bad metal may occur in proximity to an orbital selective Mott transition. This is where at least one band (orbital) is a Fermi liquid and another is a bad metal. This would mean that there are two different coherence temperatures. 
• The emergence of a single low-energy scale, common in both bands, as is seen in DMFT.
• The spin-freezing temperature.

Finally, how does the stability of the Hund's metal change with the number of orbitals?
Figures in this post suggest that the Hund's physics is more pronounced with increasing the number of orbitals. However, that may be because the critical U (and thus proximity to the Mott insulator) changes with the number of orbitals and all the curves are for the same U.

It's not complicated. It's Complex!

When is a system "complex"?
Even though we have intuition (e.g. complexity is associated with many interacting degrees of freedom) coming up with definitive criteria for complexity is not easy.

I just finished reading, Complexity: A Very Short Introduction, by John Holland.
His perspective is that a system is "complicated" if it has many interacting degrees of freedom, but is "complex" if in addition it exhibits emergent properties.
The criteria for emergence is the existence of new hierarchies, containing new entities or agents (defined by the formation of boundaries) that are coupled by new interactions, and described by new "laws".

Holland distinguishes complex physical systems (CPS) from complex adaptive systems (CAS).
The latter involve elements (agents) that can change (learn or adapt) in response to interactions with other agents.
Cellular automata and pattern formation in biology are CPS, whereas genetic algorithms, economics, and sociology are examples of CAS.

The book gives a rather dense (but worthwhile) introduction to key concepts in complexity theory including the emergence of specialists (e.g., division of labor, according to Adam Smith in economics), the role of diversity, co-evolution (e.g. Darwin's orchid and moth), and evolutionary niches (fixed points of Markov matrices!).

Holland smoothly flits backwards and forwards between examples in biology, economics, linguistics, and computer science.

Holland's definition of emergence is consistent with how I think in condensed matter. For example, the formation of weakly interacting quasi-particles in a Fermi liquid. The emergent "boundaries" define the spatial size of the quasi-particle.
What struck me is that the interactions should be viewed as emergent, just as much as the quasi-particles.
For example, if we start with quarks and QCD (quantum chromodynamics), then at "low" temperatures and densities, nucleons form and the nuclear force emerges.

How do you get in a productive zone?

We all want to increase our productivity. But too often we are distracted, procrastinate, stressed, or waste time going down dead ends.
I think there are two distinct kinds of productivity.
The first is creative, where we can clearly conceive a project, solve a problem, or draft a useful outline.
The second is the actual completion of a task, whether writing a paper or report, or making corrections, ... This is less creative and more mundane, but can consume large amounts of time, particularly if one stops and starts on the task many times.

How might you increase your productivity?
I think this is quite personal and maybe even somewhat random.
It might be very different for different people. It can be different at different times.
Factors to consider include the following.

Physical space and environment. 
Some people need a regular quiet work space that is free from distractions. Others will function well in a noisy cafe or an open plan office, maybe with headphones with loud music!

Time.
Some people function well with deadlines. Others crumble under the pressure. Some work well with short bursts during the day. Others need to block out a day or even a week to focus on something.

Involvement of others.
Some people will work best alone on a task, with minimal interactions with others. Others will barely function without input and feedback from others at many points in the process.

Good managers are sensitive to this diversity of needs and will aim to provide the appropriate environment for different individuals.

This post was stimulated by a recent experience how something came together and I was able to get a lot of work done on a specific task during a couple of plane flights. This seemed a bit random because these days I rarely work on flights because it is really non-productive.

What do you think?
What helps you get in the right "zone"?

Square ice on graphene?

As I have written many times before, water is fascinating, a rich source of diverse and unusual phenomena, and an unfortunate source of spurious research reports.
Polywater is the classic example of the latter.
I find the physics particularly interesting because of the interplay of hydrogen bonding and quantum nuclear effects such as zero-point motion and tunneling.

There is a fascinating paper
Polymorphism of Water in Two Dimensions
Tanglaw Roman and Axel Groß

The paper was stimulated by a Nature paper that claimed to experimentally observe square ice inside graphene nanocapillaries. Such a square structure is in contrast to the hexagonal structure found in regular three-dimensional ice.
Subsequent, theoretical calculations claimed to support this observation of square ice.
Here the authors use DFT-based methods to calculate the relative energies of a range of two-dimensional structures for free-standing sheets of water (both single layer and bilayers) and for sheets bounded by two layers of graphene.

The figure below summarises the authors results for free-standing layers showing how the relative stability of the different water structures depends on the area density of water molecules [which varies the length and strength of the hydrogen bonds].

On the science side, there are several interesting questions arise.
How much do the results depend on the choice of DFT functional used [RPBE with dispersion corrections]?
Would inclusion of the nuclear zero-point energy modify the relative stability of some of the structures, as it does for the water hexamer?
Quantum nuclear effects are particularly important when the hydrogen bond length [distance between oxygen atoms] is about 2.4 Angstroms. [I am not quite sure what area density this corresponds to for the different structures].

On the sociology side, this paper is another example of a distressingly common progression:
1. A paper in a luxury journal reports an exotic and exciting new result.
2. More papers appear, some supporting and some raising questions about the result.
3. A very careful analysis reported in a solid professional journal shows the original claim was largely wrong. This paper attracts few citations because the community has moved on to the latest exciting new "discovery" reported in a luxury journal.

I thank Tanglaw Roman for helpful discussions about his paper.