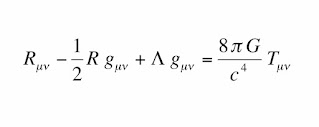A challenge in understanding and discussing emergence is that it means different things to different people. This is not surprising given emergence involves diverse and complex phenomena, occurs in a wide range of contexts, and is of interest to people in a diverse range of fields. Recently, I have started to be more precise about how emergence might be defined.
The subject interests philosophers, but it is hard for physicists to glean insights from (and critique) what philosophers say. I find the following article from 2011 by Bei Lok Hu, helpful.
Emergence: Key physical issues for deeper philosophical inquiries
Hu is not a condensed matter physicist. He is more interested in emergence from its relevance to quantum decoherence and the possibility of space-time being emergent leading to a theory of quantum gravity. Thus, the article is a good entry into literature that I am not familiar with.
Hu gives a nice summary and critique of some of the main philosophical discussions and issues. Here are a few things I have grasped so far. With respect to defining what emergence is Hu writes about three "senses of emergence". The first is below.
Emergence in the sense of difference in manifestations– Role of coarse-graining:
* Different manifestations at different levels of structures, hierarchical in form, and corresponding interactions.
* Requires the identification of the range and precision of measurement, thus interfaces necessarily with an observer’s probing ability and observation range. Effective field theory is of this nature.
* Stability of emergent structures depends on the degree of coarse-graining
* Robustness of emergent structures against the variation of coarse-graining.
(Vaguely in philosopher’s language, the first two bullets correspond to novelty, and the latter two correspond to autonomy.)
I note that this definition of "novelty" is different to mine. I take the plainer definition that at higher levels the system has a property that it does not have at a lower level. A drop of water is wet, but a single molecule is not. A brain is conscious, but a single neuron is not. A lump of solid let is a superconductor, but a few atoms of lead are not.
This illustrates how the same word can mean different things to physicists and philosophers. Other examples include "reductionism" and "fundamental".
An important work that engages both physics and philosophy perspectives is "Is More Different? Emergent Properties in Physics," Oxford University DPhil thesis, by Paul Mainwood.
Mainwood summarizes, “... systemic properties are novel, if and only if it is practically impossible to derive them from the microphysical properties mentioned in microphysical supervenience.” ([40] p. 30)
Three proposals of novelty were examined by Mainwood ([40] Sec. 1.5):
1) a failure of intertheoretic reduction;
2) an impossibility of deducing the systemic properties from the properties of the parts; or
3) a failure of mereological supervenience.
The approaches appeal to three entirely separate distinctions between the properties of parts and wholes; thus according to Mainwood, there are three entirely different sets of criteria for emergence.
Like me, Hu suggests ontology [reality] should come before epistemology [how we know]. Whereas, philosophers tend to start with epistemology and then try to use that to understand emergence. Understandably, consciousness and the philosophy of mind is a big thing for philosophers. It is often used a starting point for discussions about emergence. However, given consciousness is such a thorny, slippery, and difficult problem, to understand emergence it would be better to start with concrete and tractable examples from physics, such as emergence in condensed matter.
The final sentence of the acknowledgements in the paper is poignant, amusing, and tragic.
This kind of non mission-driven, non utilitarian work addressing purely intellectual issues is not expected to be supported by any U.S. grant agency.