Why is hype bad?

There is no doubt that the level of hype in science is increasing. You see it in grant applications, university press releases, introductions and conclusion in papers (especially in luxury journals), talks, ... Hype is also a broader problem in society, including in the business world and politics.

Why is hype bad for science?
Some will say something like, ``I agree that it is not good, but we have to do it to survive. Anyway, we all know what is really true and so it does not matter..."

However, I think there are many problems, particularly for the long term flourishing of science.

Waste of time
Figuring out that a ``hyped'' result or research field is actually just hype can take significant time. This is particularly true if one actually tries to reproduce a result and discover all the problems.

Mis-allocation of resources
Researchers, students, and funding agencies flock to hyped fields. However, it can take quite a while and a lot of money for the community to come to the consensus that things are not going to live up to the hype. This is compounded by the fact that people whose careers are enhanced by a hyped result or field are not going to back down too easily and are going to want to keep things going, at least until the next big thing comes along.

Obscuring or hiding problems that need to be solved to make real progress
Making real and significant progress in science is very hard. Every technique has its limitations. Every result involves some uncertainty. Turning science in the lab into a commercially viable technology may arguably be even harder. The obstacles are many. The best way to progress in science and technology is to clearly and honestly state the problems and challenges. This is one of my many concerns about functional electronic materials.

Intellectual integrity
Science is all about intellectual integrity. Losing our credibility with broader society won't be good for science or for society, particularly when it comes to developing well-informed public policy.

Noel Hush (1924- 2019): pioneering theoretical chemist

I was sad to hear last week that Professor Noel Hush died at age 94. Noel [also known as Prof.] was a pioneer in theoretical chemistry and chemical physics. He had a profound influence on both fields, particularly in their development in Australia.

Arguably his greatest scientific contribution was in the theory of electron transfer. Depending on where you are from this is called Hush-Marcus theory, Marcus-Hush theory, or Marcus theory. In particular, in 1958 Hush derived one of the most important equations in chemical physics, which can be used for design principles for functional electronic materials. A key concept here is the notion of diabatic states.

I had the privilege of knowing and working with Prof. Hush on and off over the past decade. As I made an adiabatic transition from condensed matter into chemical physics Prof. Hush provided a lot of encouragement, wisdom, perspective, and ideas. He strongly believed that theoretical chemists and condensed matter theorists could have mutually beneficial interactions. Together with Jeff Reimers and Laura McKemmish, we co-authored seven papers together. The last papers were published when Noel was 90 years old!

Besides his significant legacy of scientific knowledge, there is an incredible legacy of people that he taught, supervised, mentored, encouraged, and collaborated with.

There is an interesting interview of Prof. Hush about his life by Robyn Williams from 2011.

Emergence and complexity in social systems

Emergent phenomena occur in social systems. For example, self-organisation, power laws, networks, aggregation/segregation, political polarisation, political revolutions...
Can lessons from condensed matter physics help at all in understanding and modeling of social systems? Can analogies from social systems help non-scientists understand some of the basic ideas in condensed matter?

In two months I am giving a  seminar in a new UQ multi-disciplinary seminar series, Futures of International Order. In preparation, I am slowly engaging with relevant literature, particularly the work of Scott Page, including his course on Model Thinking at Coursera. The NetLogo software is helpful for exploring a range of simple models.
However, before plunging in here are a few tentative thoughts of ideas that might connect with condensed matter, in the vein of reviews such as

Physics and financial economics (1776–2014): puzzles, Ising and agent-based models 
Didier Sornette

Statistical physics of social dynamics 
Claudio Castellano, Santo Fortunato, and Vittorio Loreto

Emergence occurs in systems with many interacting components. In social systems, the components are human agents. They can aggregate into emergent entities such as neighbourhoods, institutions, and communities. Associated with these new entities are new scales of size (number of agents), length, time, and connectivity. New effective interactions between entities can also emerge. Even knowing all the details of the system components and the interactions it can be very difficult to predict the properties of the whole system. Surprises are common. Humility is needed.

Qualitative changes can occur due to small quantitative changes in a system parameter.
In condensed matter examples are phase transitions between different states of matter.  Furthermore, these changes can be directly seen as discontinuities or singularities in observables. Order parameters can quantify the changes. In social systems, similar phenomena are sometimes called tipping points.

Universality versus particularity
Close to a critical point for a phase transition most of the details of the system components and their interactions do not matter. Properties such as critical exponents are independent of most details. This is wonderful for theory because one can describe large classes of diverse systems with the same model/theory and one does not have to know all the details of the system.
Similar issues of universality are also relevant when one considers phenomena at different length scales. For example, one does not need to know anything about the atoms (even their existence!) in a crystal to develop a theory of elasticity or the propagation of sound waves.
When it comes to social systems there are a wide range of phenomena that can be potentially described by the same model. For example, Miller and Page point out that the essence of the standing ovation problem is how a binary choice (sit or stand) is influenced by the behaviour of one's neighbours. This is similar to choices as to whether to join a riot, take illegal drugs, or whether to vote of political party A or B.

Mental health in academia

Even though I have not posted about it for a while, mental health continues to be on my radar. I monitor my own mental health carefully and generally things are going well. Tragically, I still meet many in academia struggling with the issue. It is also in the news because of the recent death by suicide of Princeton economist, Alan Krueger. A few months ago, Stanford theoretical physicist, Shoucheng Zhang, also died by suicide.

The Chronicle of Higher Education has an article about how Krueger's death is prompting conversations about how the culture of academia can be unconducive to mental health.

Last week there was an excellent New York Times Opinion piece by Lisa Pryor
Mental Illness Isn’t All in Your Head 
A “formulation” gathers the biological, psychological and social factors that lead to a mental illness — and offers clues to the way out of suffering.

Orbital-selective bad metals

Alejandro Mezio and I just posted a preprint
Orbital-selective bad metals due to Hund’s rule and orbital anisotropy: a finite-temperature slave-spin treatment of the two-band Hubbard model

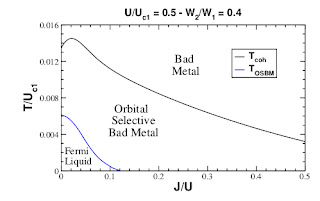
The central result is shown in the Figure below. It shows the phase diagram of the metallic phase as a function of temperature and the Hund's rule interaction J in a system with two bands of differing bandwidth. Uc1 ~ W1 is the critical interaction for a Mott insulator in a one band system with bandwidth W1.
The system is a Hund's metal in that the strong correlations arise from J and not from proximity to a Mott insulating phase (note that U=0.5Uc1).
In the orbital-selective bad metal, one of the bands is a coherent Fermi liquid (with well-defined Fermi surface) and the second (narrower) band is a bad metal.

Two things that I find particularly interesting are the following.

Stability of the bad metal and the orbital-selective bad metal are enhanced by increasing J and/or by increasing band anisotropy.

The temperatures at which the bad metals occur is orders of magnitude smaller than the Fermi temperature for the corresponding non-interacting system (being of the order of W1~ Uc1).

We welcome comments.

Imaging orbital-selective quasi-particles in a Hund's metal

Over the past two decades, a powerful new technique has been developed to determine quasi-particle properties in strongly correlated electron systems, based on STM (scanning tunneling microscope) measurements. Quasi-particle interference (QPI) has proved to be particularly useful for studying cuprates (e.g. in revealing the d-wave pairing) and now for iron-based superconductors. The basic physics is as follows. One measures the changes in the local tunneling density of states N(r,E), associated with a single impurity that scatters quasi-particles with a change in momentum q. Then the Fourier transform of this change is

The text above is taken from a nice paper
Imaging orbital-selective quasiparticles in the Hund’s metal state of FeSe 
A. Kostin, P.O. Sprau, A. Kreisel, Yi Xue Chong, A.E. Böhmer, P.C. Canfield, P.J. Hirschfeld, B.M. Andersen and J.C. Séamus Davis

They show theoretically that the intensity of the interference pattern is quite sensitive to the quasi-particle weights of the different d-orbital bands. The experiments are consistent with

The key figure is below. It shows shaded intensity plots of the change in DOS as a function of wavevector. The central column is experimental data with E increasing from -20 meV to +15 meV as one goes down the column. The left and right columns show theoretical values for the same quantities, calculated with all the quasi-particle weights Z=1 (left) and the Z values above (right).   

   

The large variation between the Z values for different orbitals shows how the effect of the correlations are orbital selective.

The same Z values were used by the same cast of characters in a study of the superconducting state that showed orbital selectivity played a key role in the Cooper pairing, including the significant variation of the energy gaps over the different Fermi surfaces. The quantitative agreement between experiment and the associated theory is quite impressive.

I thank Alejandro Mezio for bringing the papers to my attention.

Why is quantum matter so interesting?

Last year Ben Powell wrote a Perspective for Science, The Expanding Materials Multiverse. It begins with a nice statement about why quantum condensed matter is so interesting, exciting, and challenging.

High-energy physicists are limited to studying a single vacuum and its excitations, the particles of the standard model. For condensed-matter physicists, every new phase of matter brings a new “‘vacuum.” Remarkably, the low-energy excitations of these new vacua can be very different from the individual electrons, protons, and neutrons that constitute the material. The materials multiverse contains universes where the particle-like excitations carry only a fraction of the elementary electronic charge, are magnetic monopoles, or are their own antiparticles. None of these properties have ever been observed in the particles found in free space. Often, emergent gauge fields accompany these “fractionalized” particles, just as electromagnetic gauge fields accompany charged particles. On page 1101 of this issue, Hassan et al. provide a glimpse of the emergent behaviors of a putative new phase of matter, the dipole liquid. What particles live in this universe, and what new physics is found in this and neighboring parts of the multiverse?

There is also a nice figure which makes an everyday analogy to illustrate different states of matter.

Ten key ideas about condensed matter physics?

I am slowly working towards writing a Condensed Matter Physics: Very Short Introduction.
But first I am trying to clarify my audience and goals. Some earlier posts have helped me clarify this.

My intended audience is probably not you! Rather it is a person who wants to get the flavour of what CMP is actually about.  Examples might include a smart final year high school who wants to study science at university, or a first-year chemistry undergraduate, or an economics graduate, or a sociology professor, ...

My goal is to show that CMP is intellectually exciting, intellectually challenging, and intellectually important.

The VSI format is 8-10 chapters and 30-35 thousand words. It is meant to be written in the style of an engaging essay not a technical paper.

My plan is to basically have one clear and specific idea that I want to communicate in each chapter. I am thinking that in order to increase interest and comprehension that for each chapter I will aim to include.

An easily understandable analogy to illustrate the main idea.
A few relevant and illuminating figures.
An interesting historical anecdote.
An example of a technological application.
An example of cross-fertilisation to another field of science.

So here is the current version of my chapter headings and the main idea(s) I want each chapter to communicate.

1.     What is condensed matter physics?

CMP is concerned with studying and understanding material systems composed of large numbers of atoms. How do the properties of the system emerge from the properties of the constituent atoms and the interactions between them? It is a multi-faceted approach to studying materials and involves a unifying set of concepts. Quite abstract ideas and concepts can be quite powerful for understanding quite practical systems.

2.     A plethora of states of matter

Even for the simplest materials, there is a multitude of different phases, i.e. qualitatively different states of matter. Transitions between distinct phases are defined by discontinuities in properties. Phase diagrams encode what phase is stable under specific external conditions such as temperature, pressure, and magnetic field.

3.     Symmetry matters

Distinct phases are associated with distinct ordering of the system. A unifying concept to distinguish and classify different phases and their associated ordering is how they differ in the type of symmetry that they have. What different classes of symmetry are mathematically possible significantly constrains what is physically possible.

4.     The order of things

The type and quantity of order and the broken symmetry in a distinct state of matter can be described by a small set of numbers represented by the “order parameter’’.

5.     Adventures in flatland

Confining a material to one or two dimensions can lead to new states of matter. Furthermore, imagining a world of variable dimension can actually lead to a better understanding of materials in our three-dimensional world.

6.     The critical point: details do not matter

Under a very special set of external conditions, a phase transition is not associated with discontinuous properties. These conditions are represented by the critical point in the phase diagram.  Very different material systems can have the same properties close to the critical point. Understanding this universality requires looking at the system at many different length scales.

7.     Quantum matter

The weirdness of quantum theory is most commonly manifest at the level of single atoms and molecules. Surprisingly, quantum effects can also be seen “with the naked eye” in states of matter such as superconductors and superfluids.

8.     Topology matters

Abstract ideas about shapes help us understand spatially non-uniform broken symmetry states. They also lead to new states of quantum matter, that do not involve broken symmetry.

9.     Emergence matters

Condensed matter physics is all about emergence: the sum is greater than the parts. From a system composed of many interacting components new (often unanticipated) properties, concepts, and organising principles emerge. Reality is stratified.

10.  Future challenges

Almost all new states of matter are discovered by experiment and often by accident rather than being predicted theoretical. An open question and challenge is to what extent one can predict new states or to design materials with specific properties. There are significant open challenges in all facets of CMP: synthesis, characterisation, measurement, computation, and theory. Finally, given the great success of CMP at understanding emergence in complex systems a challenge is to adapt the approach and concepts to other complex systems, ranging from biology to sociology.

I welcome feedback.
But keep in mind the audience.
I do not want to add material, but perhaps even cut material (e.g. chapter 8).

What do you wish non-CMP people understood about CMP?

Generalised rigidity is a key concept

What are some of the most important concepts in condensed matter physics?
In a recent comment on this blog Gautam Menon suggested that one of them is that of generalised rigidity, i.e. the elasticity of order parameters associated with broken symmetry phases.

 A while ago I wrote a post trying to introduce Phil Anderson's discussion of the concept.
Thinking about this made me appreciate just how important and useful the concept is.

Basically, generalised rigidity quantifies how the free energy of a system varies when introduces spatial variations in the order parameter. These variations can result from boundary conditions, fluctuations, or topological defects.

Depending on the type of broken symmetry there are just a few parameters, maybe only one, involved in defining the rigidity. One is looking at "linear" response and so symmetry determines how many different terms one can write down that are second order in a gradient operator.

A concrete example is the Frank free energy density associated with non-chiral nematic crystals.

Here n is a unit vector (the order parameter) and there are just three parameters and K1, K2, and K3. The three terms represent pure splay, bend, and twist, respectively. Spatial uniformities are at the heart of liquid crystal displays.

Historical aside. It is impressive that Frank wrote this down in 1958, without any reference to Landau.

For s-wave superconductivity and superfluids such as 4He, there is just one parameter, known as the superfluid stiffness or superfluid density. This is the coefficient of the gradient term in the Ginzburg-Landau theory and determines the superconducting "coherence length".

The generalised rigidity is also important because it is central to the renormalisation group theory of critical phenomena, which start with Ginzburg-Landau-Wilson functionals (effective actions). For most cases, one discovers that higher order gradient terms are "irrelevant'' to long wavelength properties and the rigidities are renormalised by fluctuations.

The spin stiffness is the only parameter (energy scale) that appears in a non-linear sigma model treatment of ferromagnetism and antiferromagnetism. The model is sufficient to describe all of the long-wavelength and low-energy properties.

The XY model also involves just one parameter, the rigidity.  From this model one gets the Kosterlitz-Thouless transition.

Note that for both the non-linear sigma model and XY model in one and two dimensions there is no long-range order (symmetry breaking) [Mermin-Wagner theorem] yet the rigidity still has meaning.

The rigidity also determines the emergent length scales in these systems, including the size of topological defects such as vortices, skyrmions, disinclinations,....

A nice detailed discussion of much of the above is in Chaikin and Lubensky, particularly chapter 6.