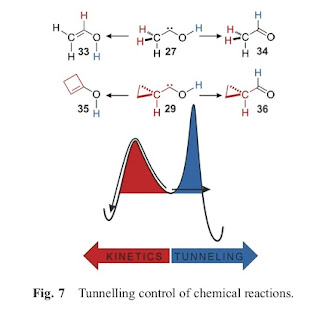
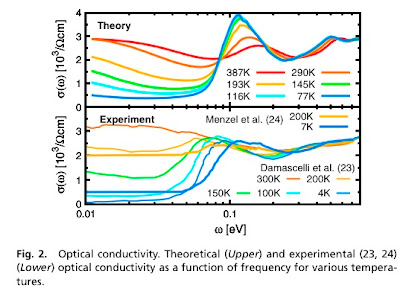
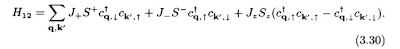How to finish your Ph.D thesis

Just write it!
Stop procrastinating. Take responsibility.
Don't wait for permission, guidance, or feedback from your supervisor, advisor, committee, or anyone else.
The more you have written and "complete" the greater the pressure on the supervisor, department, and university, to o.k. submission of the thesis.

With supervisors who are tardy/slack/lazy/negligent/disorganised about feedback make sure meetings, submissions of drafts, and requests for feedback are documented in emails.

Another crazy metric?

I have been looking at some books about better writing since next year I am going to be giving a couple of workshops on this. 

I was really intrigued that one book mentioned the Flesch Reading Ease Score which is defined by the equation:

A sign that this is a "widely accepted" metric is that it is incorporated in Microsoft Word.

The main thing that bothers me is the number of significant figures in the coefficients.

But also, surely you could devise the metric so that it actually does give values in the range 0-100, like most guides claim. Pathological text can produces negative values or values greater than 100.

Correlation or causation?

This xkcd cartoon features in an interesting article in the Economist Triumph of the nerds about how the internet has changed the world of cartoons.

Deconstructing excited state dynamics in a solvent

What determines the excited state lifetime of a chromophore in a solvent?
What are the relative importance of the polarity of the solvent [dielectric relaxation time] and the viscosity?

The key physics associated with the solvent polarity is that the dipole moment in the ground and excited states are usually different and so the solvent relaxes and there is an associated redshift of the emission. The viscosity is particularly relevant when there is intramolecular twisting and this motion is usually overdamped.

This problem is of fundamental interest because it concerns overdamped quantum dynamics.
It is of applied interest because significant biomolecular sensors make use of the sensitivity of specific chromophores [e.g. Thioflavin-T binding to amyloid fybrils].

Two recent papers from Dan Huppert's group raise three important questions for me.

An Accounts in Chemical Research
Molecular Rotors: What Lies Behind the High Sensitivity of the Thioflavin-T Fluorescent Marker?
raises the question:
1. What is unique about Thioflavin-T? 
How are the photophysical properties fine tuned?

The authors give convincing arguments as to why Thioflavin-T works. Some of these are reviewed in this earlier post.

However, given there are lots of other chromophores which undergo excited state twisting to dark states [see e.g., this review] it is not clear to me why all these other molecules don't work just as well as Thioflavin-T?

The excited state dynamics is interpreted in terms of the figure below where there are two distinct excited singlet states:

A local excited state (LE) and a twisted intramolecular charge-transfer (TICT) state.

2. Are the LE and TICT states distinct? 

In the simplest two-diabatic state picture there is a single excited state and as the chromophore twists this smoothly evolves from a bright state at the Franck-Condon point to a dark TICT state. This is what Seth Olsen and I found for the chromophore of the Green Fluorescent Protein [see our recent J. Chem. Phys. paper].

The paper
Temperature and Viscosity Dependence of the Nonradiative Decay Rates of Auramine-O and Thioflavin-T in Glass-Forming Solvents
reports that over more than three orders of magnitude the excited state lifetime is proportional to the viscosity and to the dielectric relaxation time.

This raises a subtle issue: causality vs. correlation. The authors point out that in the simple theory of a dielectric liquid the viscosity and the dielectric relaxation time are proportional to one another.

3. Can one separate out the respective contribution of the polarity of the solvent and of the viscosity?

There are two distinct reaction co-ordinates here: the motion associated with each is overdamped. One co-ordinate is the intra-molecular twisting of the solute and which couples to the viscosity of the solvent. The other co-ordinate is the local electric polarisation of the solvent which couples to the dipole moment of the excited state.

Rocket science for children

Yesterday I did some science demos at a kids holiday club, using the Coke-Mentos fountain. Previous efforts led to the post Developing science demonstrations that actually teach science. It is fun and cool to do spectacular demonstrations that cause kids to go "Wow!" and think that science is "fun". But these also need to be a vehicle to teach something about critical thinking and the process of doing science.

Small initiatives can help. For example, I had one child record the height of each of the fountain, that was estimated by the group. This emphasized that measurement, error estimation, record keeping, and comparisons are key parts of doing science.

Aside: Yesterday I thought the Coke-Mentos fountain was higher than last time, particularly for diet Coke. I suspect the fact that is was a hot day helped, increasing the solubility of the carbon dioxide?

We also did Film canister rockets which the kids always enjoy.
I found it amusing that the kids ran off and told their friends they were doing "rocket science".

My questions about condensed phase photochemistry?

For the excited state dynamics of a specific chromophore in a solvent what are the essential degrees of freedom (electronic, vibrational, and solvent) that must be included in a model Hamiltonian?

What determines if the excited state dynamics is classical, semi-classical, or fully quantum? Under what conditions does the Born-Oppenheimer approximation break down?

For a specific photochemical reaction what are the relevant vibrational degrees of freedom? What determines the relative importance of stretching, torsional, and pyramidal vibrations?

What determines the branching ratio for passage through a conical intersection? Relevant parameters may be the slope at the intersection, slanting, size of the wavepacket, and the distance of closest approach (impact parameter)

What is the interplay of the electronic, vibrational and solvent degrees of freedom in excited state dynamics?

What determines the relative importance of the viscosity and the polarity of the solvent for the dynamics? What is the role of the spatial inhomogeneity of the solvent?

In the presence of a solvent what are respective criteria for the localization/delocalization of electronic and/or vibrational excitations over different parts of the chromophore?

What are definitive experimental signatures of delocalization?

What are definitive experimental signatures of breakdown of the Born-Oppenheimer approximation?

What is the role of the solvent in non-adiabatic processes?

Questions about protein folding

What is the physical code that relates the amino acid sequence to a proteins native structure?
How do proteins fold so fast?
Can protein structure be computationally predicted?

These are highlighted as key questions in a nice readable review in Science The Protein Folding problem, 50 years on by Ken Dill and Justin MacCallum.

The article gives a sober assessment of limited but significant achievements and the substantial challenges ahead.

The puzzle of linear magnetoresistance in topological insulators

Tony Wright brought to my attention a nice (brief) review paper on the arXiv
Magnetotransport and induced superconductivity in Bi based three-dimensional topological insulators
M. Veldhorst, M. Snelder, M. Hoek, C. G. Molenaar, D. P. Leusink, A. A. Golubov, H. Hilgenkamp, A. Brinkman
[published version is here].

In passing, I note there is a brief section on Shubnikov de Haas oscillations and the Berry phase. A more extensive discussion can be found in a recent preprint by Tony Wright and I.

Here I briefly discuss the very nice section about linear magnetoresistance (LMR) (i.e. a magnetoresistance that increases linearly with magnetic field, in contrast to the quadratic increase characteristic of regular metals) that have been observed in Bi-based topological insulators. This was of particular interest to me because I previously posted about the puzzle of linear magnetoresistance in Ag2Te [which may or may not be a topological insulator]. Similar issues and theoretical models arise here.

The physical origin of the observed magnetoresistance is also not clear.

First, it is hard to distinguish the contributions from the bulk and the surface conductivity. But, the authors suggest "it seems unlikely that the LMR ... originates from the surface states alone".

Second, the authors raise questions about whether the materials are really in the lowest Landau level, as assumed in Abrikosov's quantum magnetoresistance model. They then critically examine a model by Wang and Lei that requires a linear dispersion and a small Zeeman splitting. This can be distinguished from Abrikosov's model via the density dependence of the LMR.

Two more theoretical models are then discussed.

So, the challenge is to come up with definitive experiments to rule out some of the theories.

I thank Xiaolin Wang for interesting me in this problem last year. His experimental results are reported in this PRL and APL.

A historian on impact factors

Following  my post Impact factors have no impact on me, a question was raised about the role of impact factors in different disciplines and whether they are useful for making comparisons.

Factoring impact describes a history Ph.D student's perspective on first encountering impact factors.

Is ionic polarizability a primary or secondary cause in cuprates?

Distinguishing cause and correlation in complex systems is always a tricky matter.

There is an interesting preprint
Ion-size effects in cuprate superconductors - implications for pairing
B.P.P. Mallett, T. Wolf, E. Gilioli, F. Licci, G.V.M. Williams, A.B. Kaiser, N. Suresh, N.W. Ashcroft, J.L. Tallon

For a large family of cuprates they observe correlations between the basal plane area of the unit cell, the Heisenberg antiferromagnetic exchange J, the maximum superconducting Tc, and the total electric polarizability of the ions.

The main result from this rather impressive systematic study is in the Figure below

The upper graph shows that Tc (max) decreases with increasing J, contrary to what one might expect from spin fluctuation mediated (or RVB) type pictures of superconducitivity (see e.g. this paper which found the pairing amplitude scaled roughly with J).

The lower graph shows that Tc (max) increases with increasing ionic polarizability. The authors then make the claim (first proposed by Neil Ashcroft, one of the authors) that the superconductivity results from pairing via collective excitations of ionic polarizability, rather than via spin fluctuations.

However, I wonder about a different and less radical interpretation.
Assume the maximum Tc does not simply scale with J. One might also worry about what is happening to the tight binding parameter t, since this will also decrease with decreasing unit cell area.

Then remember that the cuprates are charge transfer insulators. The one band t-J model is derived from a two-band model with both p (oxygen) and d (copper) orbitals. The effective J is given by

Background: the figure below taken from this review illustrates the underlying lattice and energy levels.

Hence, as the ions become more polarised the denominator will increase and J will decrease, as is observed here.
Is this less radical hypothesis consistent with the evidence?

Acknowledging a sad reality

Bei-Lok Hu has a nice paper on the arXiv, Emergence: Key physical issues for deeper philosophical inquiries. The acknowledgements end with the poignant (and sad) observation:

 This kind of non mission-driven, non utilitarian work addressing purely intellectual issues is not expected to be supported by any U.S. grant agency.

A key concept in condensed matter: energy scales

To the experienced this post may seem a bit basic but I think it does concern something really important that students must learn and researchers should not forget.
It is a very simple idea but when continually applied it can be quite fruitful. Understanding and teaching condensed matter became a lot easier when I began to appreciate this.

In considering any phenomena in condensed matter it is important to have good estimates (at least within an order of magnitude) of the different energy scales associated with different interactions and effects.

I give several concrete examples to illustrate.

To understand why Fermi liquid theory works so well for elemental metals (sodium, magnesium, tin, ...) the first step is estimating the Fermi energy, the thermal energy (k_B T), the Zeeman energy in a typical laboratory field, ...

A step towards the BCS theory of superconductivity was appreciation of the profound disparity of energy scales, condensation energy much less than k_B T_c comparable to the energy gap, much less than a phonon energy, which in turn is much less than the Fermi energy.
Similarily in the Kondo effect one has the emergence of a low energy scale that is much less than the Fermi energy and the antiferromagnetic Kondo coupling J.

In my own research this issue was a key step in realising that the metallic phase of organic charge transfer salts was a bad metal and could be described by dynamical mean-field theory of the Hubbard model. Specifically it was a puzzle as to why the thermal energy at which the Drude peak disappeared was so much less than the Fermi energy. I first discussed the issues here.

Furthermore, I often find that this simple approach can often rule out exotic phenomena that theorists propose or simplistic explanations that experimentalists make. For example, this post discusses how phenomena discussed in several theory papers require magnetic fields orders of magnitude larger than laboratory fields.

Some may say this skill and approach is important in any area of physics (e.g. fluid dynamics, nuclear physics, optics, ...). However, I suspect it is even more crucial in condensed matter because of the incredible diversity of interactions and emergent phenomena and the associated diversity of energy scales,

Advice to ambitious undergraduates

There is a useful post For the ambitious prospective Ph.D student: a guide.
It is written by Rachael Meager, an undergraduate at Melbourne University, about how Australian students can get into top 10 Economics Ph.D programs, largely in the USA.
Much of the advice is also relevant to science and engineering programs, and I suspect beyond Australia.
It is also relevant to Australian students who want to get a high first class honours result so they can get a Ph.D scholarship within Australia, in a leading research group.

I thought it was cute she recommended writing comments on faculty blogs to make them aware of your existence, interest, and sophistication. Lots of economics faculty write blogs.

In the Australian context I would also suggest that students consider limiting or quitting part-time jobs (McDonald's etc.) unless it is a matter of not eating.
The average Australian undergraduate works something like 10-20 hours per week.
It is simply not possible to do this and expect to have a stellar undergraduate performance.
Take out a student loan or cut back on the i-phone, clubbing, car, overseas holidays....

Having a long commute is also something to avoid.

As usual you have to decide what is really important to you and what short-term sacrifices you are willing to make to achieve long term goals.

BTW: the preceding post on the same economics blog by Rohan Pritchford about the state of "tenure" in Australian universities is also a good read.

What they don't teach you in graduate school

Doug Natelson has a nice post Things no one teaches you as part of your training which discusses some of the crucial skills that scientists (whether university faculty or industrial managers) must have but are never taught.
These include managing people, writing, being a good colleague, ...
The assumption is that these skills are hopefully absorbed by osmosis.
One could argue that they should be more explicitly taught, even if only informally.

One that is particularly important to experimentalists and I had not thought about is managing budgets. Consumables, and equipment purchase and maintenance can easily blow out. If there isn't enough money for these then a lab can grind to a halt.

Some of the comments list useful resources for helping learn some of these skills.

Physical manifestation of the Berry connection

Although I have written several papers about it I still struggle to understand the Berry phase and how it is or may be manifested in solids.
Recent reading, summarised below, has helped.

There is a nice short review Geometry and the anomalous Hall effect in ferromagnets
N. P. Ong and Wei-Li Lee

As late as 1999 Sundaram and Niu wrote down the semi-classical equations of motion for Bloch states in the presence of a Berry curvature, script F below.
(1) and (2) below. n.b. how there is a certain symmetry between x and k.

The last equation gives the "magnetic monopoles" associated with the Berry connection/. Aside: the Berry connection Omega_c is the analogue of the magnetic field. It is related to the curvature F tilde by (F tilde)_ab= epsilon_abc Omega_c.

The Berry connection is related to the Berry phase in the same sense that a magnetic field is associated with an Aharonov-Bohm phase.

The above text is taken from a beautiful paper Berry Curvature on the Fermi Surface: Anomalous Hall Effect as a Topological Fermi-Liquid Property by Duncan Haldane.

The symmetry arguments above show why the anomalous Hall effect only occurs in the presence of time-reversal symmetry breaking, e.g. in a ferromagnet.

It is interesting that Robert Karplus (brother of Martin) and Luttinger wrote down what is now called the Berry connection as long ago as 1954! (30 years before Berry!)
They called it the anomalous velocity.
The connection with Berry and topology was only made in 2002 by Jungwirth, Niu, and MacDonald.
An extensive review of the anomalous Hall effect, both theory and experiment, is here.

A sober critical assessment of computer simulations

There is a nice article on the arXiv, Simulations: the dark side by Daan Frenkel
Here is an extract to give you the flavour

Although this point of view is not universally accepted, scientists are human. Being human, they like to impress their peers. One way to impress your peers is to establish a record. It is for this reason that, year after year, there have been – and will be – claims of the demonstration of ever larger prime numbers: at present – 2012 – the record-holding prime contains more than ten million digits but less than one hundred million digits. As the number of primes is infinite, that search will never end and any record is therefore likely to be overthrown in a relatively short time. No eternal fame there. In simulations, we see a similar effort: the simulation of the ‘largest’ system yet, or the simulation for the longest time yet (it is necessarily ‘either-or’). Again, these records are short-lived. They may be useful to advertise the power of a new computer, but their scientific impact is usually limited.

The article focusses on the technical limitations (and traps) of classical molecular dynamics and Monte Carlo simulations. It would be nice if someone wrote a similar article for quantum simulations.

I learnt of the existence of the article from Doug Natelson's blog, Nanoscale views.

Wilson's ratio for strongly correlated electrons

The (Sommerfeld-)Wilson ratio is an important quantity to characterise strongly correlated Fermi liquids.

Chapter 5 of Hewson's book The Kondo Problem to Heavy Fermions describes the Fermi liquid theory of the Anderson single impurity model. One can derive the identity

which relates the impurity spin susceptibility, charge susceptibility, and the specific heat coefficient gamma.

In the Kondo regime the charge susceptibility is zero and this leads to the fact that the Wilson ratio has the universal value of exactly two.

It is interesting that one can derive the same identity for the exact (Bethe ansatz) solution to the Hubbard model in one dimension. See equation (7) in this paper by Tatsuya Usuki, Norio Kawakami, and Ayao Okiji. As a result one finds the Wilson ratio is always less than 2. As the band filling tends towards one-half the Mott insulator is approached, the charge susceptibility diverges and the Wilson ratio W tends to zero. See the Figure below.

Quantum tunneling changes chemical reactions

The dynamics of the atomic motion associated with most chemical reactions is classical. In particular, the rate of reaction is determined by the rate of thermal excitation over an energy barrier associated with the transition state (a key concept): a particular nuclear configuration which is a saddle point on the potential energy surface which contains both the reactants and products.

It is hard to find exceptions to this paradigm, e.g., where quantum tunneling below the barrier is important. Some people claim this picture breaks down for enzymes, as discussed in an earlier post. But I remain to be convinced, particularly that enzymes have evolved to make use of quantum tunneling.

However, I am convinced and fascinated by an article which does discuss some concrete exceptions to transition state theory for small molecules that have recently been discovered. Tunneling does not just lead to quantitative changes in reaction rates but different products of the chemical reaction.
There is a nice review of this work:

Tunnelling control of chemical reactions – the organic chemist’s perspective
David Ley, Dennis Gerbig and Peter R. Schreiner

One of the main points is summarised in the figure below. If one starts with the molecule in the centre then at high temperatures the reaction proceeds to the left, because that product involves the lowest energy barrier (activation energy).
However, the energy barrier to produce the molecules shown on the right is narrower. Hence, when the reaction is dominated by tunneling (i.e. at low temperatures) one gets a different product.

Is there superconductivity in the Hubbard model?

Previously, I considered the tricky problem of Does the doped Hubbard model superconductor?
I mentioned in passing a worrying quantum Monte Carlo study published in PRB in 1999

Correlated wave functions and the absence of long-range order in numerical studies of the Hubbard model
M. Guerrero, G. Ortiz, and J. E. Gubernatis

The graph below shows the distance dependence of the pairing correlation function in the d-wave channel. If superconductivity occurs it should lend to a non-zero value equal to the square of the superconducting order parameter.
It certainly looks like it tends to zero at large distances.

However, careful examination shows that it seems to have a non-zero value of order 0.001.
Perhaps, that is just a finite size effect.
But, we should ask, "How big do we expect the long-range correlations, i.e. the magnitude of the square of the order parameter d, to be?"

A cluster DMFT calculation on the doped Hubbard model (in the PRB below) gives a value of order 0.03 for the order parameter d. This means d^2 ~ 0.001 consistent with the QMC study which claims no superconductivity!

Anomalous superconductivity and its competition with antiferromagnetism in doped Mott insulators
S. S. Kancharla, B. Kyung, D. Sénéchal, M. Civelli, M. Capone, G. Kotliar, and A.-M. S. Tremblay

Similar issues arise when assessing the results of
Absence of Superconductivity in the Half-Filled Band Hubbard Model on the Anisotropic Triangular Lattice
R. T. Clay, H. Li, and S. Mazumdar

If I take the order parameter estimated by a RVB calculation reported in this PRL (by Ben Powell and myself) and square its value it predicts a long-range pairing correlation (~0.001) comparable to the extremely small values found in the numerical study claiming absence of superconductivity.

Clay, Li, and Mazumdar also mentioned the problematic observation that the pairing correlation they calculated did not increase with the Hubbard U. However, my previous post discussed how Scalapino and collaborators argued this is because one needs to factor in the quasi-particle renormalisation Z that also occurs with increasing U. For the half-filled Hubbard model this probably leads to an order of magnitude enhancement of the pairing as U increases towards the Mott insulating phase, since Z decreases from 1 to 0.3 and the renormalised P_d scales with 1/Z^2.

So, I remain to be convinced that superconductivity does not occur in the Hubbard model, both upon doping the Mott insulator or at half-filling near the band-width controlled Mott transition.

Impact factors have no impact on me

There seems to be a common view that on CVs (and grant applications) people should list the Impact Factors for each journal in which they have a paper.
To me this "information" is just noise and clutter.
I do not include it in my own CV or grant applications.
Why?

1. IFs just encode something I know already.
Nature > Science > PRL ~ JACS > Phys. Rev B ~ J. Chem. Phys. > Physica B ~ Int. J. Mod. Phys. B > Proceedings of the Royal Society of Queensland .....

2. There is a large random element in success or failure to get an individual paper published in a high profile journal. e.g., who the referees are.

3. The average citations of a journal is not a good measure of the significance of a specific paper. There is a large variance. What really matters is how much YOUR/MY specific paper in that journal is cited in the long term. Unfortunately, in most cases it is hard to know in less than 3-5 years.

4. Crap papers can get published in Nature and Science. Hendrik Schon published almost 20 papers in Nature and Science. On the other hand, Nobel Prize winning papers are sometimes published in Phys. Rev. B (e.g. giant magnetoresistance).

5. I don't need to know the actual IF of a journal with an impact factor of one or less in order to know that it is a rubbish journal. I already know that because I virtually never read papers in such journals simply because they virtually never contain anything that is significant, interesting, or valid. My "random" meanderings through the literature virtually never lead me there.

6. I remain to be convinced that reporting IFs to more than 2 significant figures and without error bars is meaningful.

I fail to see that alternative metrics such as the Eigenfactor resolve the above objections.

The only value I see in IFs is helping librarians compile draft lists of journals to cancel subscriptions to in order to save money.

I am skeptical that IFs are useful for comparing the research performance of people in different fields (e.g. biology vs. civil engineering vs. psychology vs. chemistry).

And in the end... what really matters is whether the paper contains interesting, significant, and valid results... Actually looking as some of an applicant's papers and critically evaluating them is the best "metric". But that requires effort and thought...

What did Wilson do?

Last week we struggled through chapter 4, "Renormalisation group calculations" of Hewson's book, The Kondo Problem to heavy fermions.

The focus is on Kenneth Wilson's numerical treatment of the Kondo problem, mentioned in his Nobel prize citation. Much of it still remains a mystery to me...
Here are a few key aspects. Please correct me where I am wrong or at least confused...

First, he mapped the three-dimensional Kondo model Hamiltonian into a one dimensional tight binding chain (half-line) with single impurity spin at the boundary. This simplification makes the problem more numerically tractable.

Next, he used a logarithmic discretization (in energy) of the states in the conduction band. This important step is motivated by the logarithmic divergences found by Kondo's perturbative calculation and Anderson's poor man's scaling arguments.

He then numerically diagonalises the Hamiltonian with a discrete set of states for a finite chain. One then rescales the Hamiltonian, truncates the Hilbert space, and adds an extra lattice site.

Eventually, one converges to the strong coupling fixed point and one observes an almost equally spaced excitation spectrum, characteristic of a Fermi liquid.

A surprising thing is that the rescaling parameter Lambda is set to a relatively large value of 2, compared to a value close to one, that one might expect to be needed. Wilson was clever to realise/find that such coarse graining would work so well.

Wilson extracted a large amount of information from his calculations. Here are a few important findings.

1. The impurity specific heat and impurity susceptibility had a Fermi liquid temperature dependence. The latter was given by

[This] shows that there is no residual local moment, and that the impurity spin is fully compensated. The numerical factor 0.4128 is a universal number for the s-d model, and is known as the Wilson number, w. It relates two quite different energy scales for the s-d model, T_K, which is determined from the high temperature perturbative regime, and chi_imp(0), the low temperature susceptibility associated with the strong coupling regime.

2. The Sommerfeld-(Wilson) ratio had a universal value

3. Over an intermediate temperature range (one and half decades) the temperature dependence can be fit to

This Curie- Weiss form corresponds to a reduced moment compared to the free spin form. Thus the impurity moment, even for T ~ T_K, is only of the order of 30% that of the free moment. The residual effects of the screening of the conduction [electrons] persist to very high temperatures because of the logarithmic dependence on T/T_K.

4.  The complete universal dependence with a logarithmic temperature scale is shown below

Writing effective papers

Weston Borden's article 40 years of fruitful chemical collaborations has an significant observation concerning writing effective papers: focus on the physical explanation of the results rather than on the details of the methodology.
He recounts how he he learnt this, while starting out as an Assistant Professor at Harvard, in a collaboration with Lionel Salem. Borden had performed some calculations using the Pariser-Parr-Pople (PPP) model for the electronic structure of conjugated organic molecules [for physicists an extended Hubbard model with long-range Coulomb interactions].

Lionel read my draft, and he promptly rewrote it. Lionel’s revised version, which was the one that we published, focused much more than my draft had on the explanation of the PPP results, rather than on the details of the calculations. This experience taught me a valuable lesson. Although describing the details of calculations and the results obtained from them is certainly important, it is even more important to write a clear, physical explanation of the results. 

This was also the lesson that I learned from the papers that Roald Hoffmann published in the late 1960s and early 1970s. Although it was well-known that the Extended Hückel (EH) method that Roald used was quantitatively unreliable, Roald provided such convincing qualitative explanations of his EH results that it always seemed to me Roald’s EH results must be correct.

I think these observations are just as relevant and important for physicists.

Aside: an earlier post sung the praises of Hoffmann's paper titles.

Borden then makes the important and worrying observation:

Perhaps the tremendous increase in the accuracy of electronic structure calculations during the past 40 years has had the undesirable consequence that computational chemists feel less obliged to provide the kind of detailed physical explanations of their results than Roald routinely furnished 40 years ago.

Transition from a band insulator to a bad metal

Many previous posts have considered how in a metallic phase close to a Mott insulator one can observe a crossover from a Fermi liquid to a bad metal with increasing temperature.

One observes something quite different in FeSi (iron silicide) which has been a subject of debate for several decades. Different paper titles include the following words: Kondo insulator, ferromagnetic semiconductor, unconventional charge gap, strong electron-phonon coupling, Anderson-Mott localization, singlet semiconductor, covalent insulator, correlated band insulator, ferromagnetic metal, ....

At low temperatures FeSi is a semiconductor with a gap of about 50 meV (500 K). Both the spin susceptibility and the resistivity are gapped. However,  around 200 K there is a crossover to a bad metal.
The spin susceptibility has a maximum versus temperature around 400 K and above that can be fitted to a Curie-Weiss form, suggesting the presence of local moments.
The thermopower has a maximum around 50 K with a colossal value of 700 microVolts/Kelvin, making the material attractive for thermoelectric applications. The thermopower changes sign at about 150 K and 200 K.
With increasing temperature the optical conductivity shows redistribution of spectral weight on the electron Volt (eV) scale, an important signature of strong electronic correlations.

There is a really nice paper which provides a compelling theoretical description and explanation of what is going on.
Signatures of electronic correlations in iron silicide
Jan Tomczak, Kristjan Haule, and Gabi Kotliar

The authors perform electronic structure calculations combining Density Functional Theory (DFT) [at the level of Generalised Gradient Approximation (GGA)] with DMFT [Dynamical Mean-Field Theory].
They reproduce the main features of the experimental data.

Here is some of the key physics.
FeSi is a band insulator at low temperatures.
With increasing temperature there is a crossover to incoherence, i.e. the Bloch wavevector is no longer a good quantum number.
Fe is in a mixed valence state with a mean valence (no. of d electrons) of 6.2 and a variance of 0.9.
There is a preponderance of S=1 states, contrary to earlier suggestions that FeSi is a singlet insulator.
The incoherence arises because of fluctuations in the local moment, which is to a large extent non-local.
The results are controlled by the Hund's coupling J rather than the Hubbard U, something also seen recently in other systems with orbital degeneracy [see this two-faced post or discussion of strontium ruthenate or a recent review].

40 years of collaborative quantum chemistry

There is a very nice article in the Journal of Organic Chemistry
With a Little Help from My Friends: Forty Years of Fruitful Chemical Collaborations
by Weston Thatcher Borden

Borden's career is unusual in that he has done both organic synthesis [i.e., actually making molecules] and computational quantum chemistry.

The article is worth reading for several reasons. It describes some
-interesting organic chemistry and shows how quantum chemistry has illuminated it
-characteristics of fruitful collaborations, both between theorists and between theorists and experimentalists
-interesting history and personal vignettes and perspectives

On the latter I found the following throwaway line rather disturbing and disappointing:

When I was an Assistant Professor at Harvard, unlike most of my colleagues in the Chemistry Department, Bill Doering seemed genuinely interested in talking about chemistry with me.

Unfortunately, this happens too often. I would be curious to know why Borden thinks this was. Sometimes it is because people are too "busy" and/or preoccupied with their own little world. The worst reason can be senior scientists actually lose interest in science and get consumed with funding, politics, ...alternatives to struggling to do significant research.

Some of the insights in the article justify a blog post in their own right and so I hope I will post separately about writing up quantum chemistry calculations, tunneling by carbon in organic reactions, symmetry breaking in TMM, and "different electronic states of the same molecule can have different MOs [Molecular Orbitals],..."

A paper of Borden's featured in an earlier post Seeing how degenerate radicals can be

Topological insulators get more interesting

Topological insulators (TIs) are certainly a hot topic. However, there are two things that might make one nervous about all the excitement.

1. All the materials being studied as TIs [e.g. Bi2Se3] actually aren't TIs.
What!? A TI is by definition a bulk insulator with surface metallic states that are topologically protected. However, the actual materials turn out not to be bulk insulators. On a practical level this makes separating out bulk and surface contributions, particularly in transport measurements, tricky. But, also presents an ideological problem: one is not actually studying the phase of matter one wishes one was studying.

2. One could argue that TIs are "just a band structure effect", i.e., they do not involve any quantum many-body physics.

However, these objections are put to rest by a preprint
Discovery of the First True Three-Dimensional Topological Insulator: Samarium Hexaboride
Steven Wolgast, Cagliyan Kurdak, Kai Sun, J. W. Allen, Dae-Jeong Kim, Zachary Fisk

They report electrical transport measurements that show that SmB6 is a bulk insulator with surface metallic states.
This is of particular interest for several reasons

a. The material really is a true topological insulator.
b. The material is a Kondo insulator. [Although strictly the material is in the mixed valence rather than the local moment regime.] The insulating state emerges from strong electronic correlations.
c.  This resolves long standing puzzles about previous transport measurements on this material which did not show activated conductivity at low temperatures. This can now be explained as a sample dependent contribution from metallic surface states.
d. This material was predicted to be a topological Kondo insulator by Dzero, Sun, Coleman, and Galitski.

I also note a recent paper Actinide Topological Insulator Materials with Strong Interaction.

I thank Tony Wright for bringing the preprint to my attention.

Am I missing something?

There is a paper in Science this week Flows of Research Manuscripts Among Scientific Journals Reveal Hidden Submission Patterns

The authors claim, 

Resubmissions were significantly more cited than first-intents published the same year in the same journal.... 

... these results should help authors endure the frustration associated with long resubmission processes and encourage them to take the challenge 

Then I looked at the data below to see how strong the claimed effect was.

I think the horizontal lines mark the mean and the box shows the variance.
Hence, it looks to me like citations may increase by less than 10% with resubmission.

This hardly seems on any significance to me.
But, am I missing something?

Maybe this is another issue of comparisons are in the eye of the beholder or the silly claims that journals make about their impact factors or some faculty make about their student evaluations.

The wealth of a poor man's scaling

Chapter 3 of Hewson's The Kondo Problem to Heavy fermions reviews Anderson's poor man's scaling treatment of the Kondo model.

Starting with the anisotropic Kondo Hamiltonian

one rescales the electronic bandwidth D and see how the interactions J_z and J_ and J+ rescale.

To lowest order in perturbation theory this leads to the renormalisation group equations

Solving these gives the flow diagram below

A few important consequences

1. Antiferromagnetic (AFM) interactions flow to strong coupling.

2. The Kondo energy/temperature is invariant to the flow.

3. This is an example of asymptotic freedom [interactions can weaker at higher energies].

It is impressive that Anderson did this before Wilson and Fisher used renormalisation group ideas to describe critical phenomena in classical phase transitions.

It is fascinating that the same flow equations and flows describe the Kosterlitz-Thouless phase transition associated with topological order [vortex pair unbinding] in a classical two dimensional superfluid.

The spin boson model which describes the quantum decoherence of a single qubit in an ohmic environment can be mapped to the anisotropic Kondo model and so is also described by the same flow equations [See this famous (and rather dense) review by Leggett et al.]

17 citations in 12 years in not impressive

I can fully imagine a grant reviewer, tenure or hiring committee saying that when reviewing the "impact" of a particular publication of an individual.

Furthermore, one can also say
"the paper was in PRL but it was a full 12 months between submission and publication. Clearly, he was lucky to get in PRL at all..."

But, there is a problem with all this.
These observations apply to Duncan Haldane's 1988 paper Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the "Parity Anomaly"

Haldane's paper has been receiving about 100 citations per year for the past few years.
It now has a total of 530 citations in Physical Review journals.
However, from 1988 to 1999 it received only 17 citations.
Hardly impressive.

The Kondo effect is non-perturbative

Last week we read "Beyond perturbation theory", chapter 3 of Hewson's The Kondo Problem to Heavy Fermions.

First he gives, without derivation, perturbation expressions for the impurity spin susceptibility and specific heat. The results exhibit logarithmic divergences at temperatures of the order of the Kondo temperature.

Hewson discusses some of the herculean efforts in the 1960s of people such as Abrikosov, Suhl, and Hamann, to come up with new diagrammatic techniques and summations to get rid of, or at least reduce, the divergences.
The results still have logarithmic temperature dependences. None give the Fermi liquid like dependences at low temperatures that experiments hinted at.

The Kondo effect is non-perturbative. n.b. the Kondo temperature has a non-analytic dependence on J.

What does one do?
An important insight was variational wave function proposed by Yosida in 1966.

One finds that the ground state is a spin singlet between the impurity spin and a superposition of the electrons above the Fermi sea. The binding energy has a similar non-analytic dependence on J as the Kondo temperature. Indeed if the wave function is generalised to include an infinite number of particle-hole pair excitations one finds that the binding energy is the Kondo temperature. Furthermore, the spin susceptibility is finite and inversely proportional to the Kondo temperature.

How can one describe the crossover with temperature to formation of these Kondo singlets and the emergence of the Kondo energy scale?
Anderson's poor mans scaling does that. Since it is such a profound and monumental achievement it deserves a separate post!

Postdoc in theoretical chemical physics at UQ

Seth Olsen and I are about to advertise for a postdoc to work with us at UQ. The flavour of our interests and approach can be seen in posts on this blog under labels such as organic photonics, quantum chemistry, conical intersections, and Born-Oppenheimer approximation.

A draft of the official position description is here. We anticipate an official advertisement will appear shortly. Please contact us if you are interested.

Should I change jobs?

Some of my colleagues, may say "Yes!".
However, this post is mostly concerned with moving from academia to industry and is mostly directed at graduate students and postdocs. However, some of the issues are also relevant to faculty considering a change of institution.
The issues are based on my limited experience and observations over almost three decades. I stress that I am not saying that all the realities below are right or just, only that they are realities that may need to be faced.

Its personal.
Different people have different values.
How much do you value (or don't value) independence, freedom, money, family time, flexible work hours, job "security", affirmation, geographic location, ....?
The relative value you place on such things will significantly affect what job may be suitable for you and whether and when you decide to make a change?
A job that is great for your friend may be horrible for you and visa versa.
There is no simple right answer.

Every job sucks.
or at least some of it sucks...
Read Genesis 3 and Ecclesiastes. Earning a living is tough.
The grass usually looks greener elsewhere. Stop looking for the perfect job.
Unfortunately, every job involves some frustration, some instability, some inane policies, some tedious tasks, some insufferable colleagues, some anxiety, some incompetence, some compromise, limited appreciation, and limited resources....
I concede these problems are greater in some jobs than others. However, I think they are pretty significant in any job and any institution.
The quicker you come to terms with this painful reality and learn how to cope with these challenges the greater your job satisfaction will be and may save you from making a change that just dishes up the same (or a new set) of frustrations and disappointments.

Most science and humanities Ph.D's will not get permanent jobs in academia.
Consider the brutal statistics: the number of Ph.D graduates every year vastly outnumbers the number of faculty positions. It has been that way since the 1970s and will continue to be so. Don't believe anyone who tells you otherwise.  Nevertheless, I am still pleasantly surprised at the number of people I encounter who do seem to stick at it and somehow survive, particularly with some luck, and if they are geographically flexible.

There are many intellectually challenging jobs outside academia.
If you leave, either because you have to or decide to, you have not "failed" in any sense and are not destined to intellectual mediocrity. After all, there are "brain dead" jobs both inside and outside academia. Don't let anyone look down on you.

Deal with your inner demons first.
Anxiety, difficulty getting along with colleagues, disappointment, stress, perfectionism, yearning for affirmation and appreciation, poor self-esteem, lack of confidence, lack of contentment, depression....
Don't think changing jobs is going to make these personal issues go away. They may be less acute in some jobs but they will still be there. They may be even be more acute in industry. Don't let a desire to escape these pressures drive a decision.
I wish I had dealt with such issues earlier in my career.

You may not make more money in industry than in academia.
It is certainly true that some gifted and fortunate individuals make a ton of money in industry. The former Chief Scientist of Queensland was fond of telling science students that many of the richest people in the world had science or engineering degrees. However, you are probably not going to be one of them.
It may be true that the average starting salary for a science Ph.D in industry is much greater than a postdoc salary, even some junior faculty salaries.
However, do not assume that in industry that you will make this much money (plus more) every year of your life until retirement. 
Hiring and firing, boom and bust: that is the natural cycle of high-flying industry.
I have known people who have had very high paid jobs in industry for a few years, followed by periods of unemployment or under-employment. Sometimes they have also been forced to undergo costly relocations to stay employed.
Also factor in the high cost of living [or very long commutes] that may go with high paid jobs in locations such as London, New York City, or Palo Alto.

Make a decision. Then stick to it for a definite period of time.
Will I? Won't I?
If for an extended period of time you are constantly uncertain and wanting to regularly discuss it with your family, friends, and/or colleagues it may not only drive you crazy but also them.

During a possible transition out of academia be circumspect about who you confide in
If you let many people know you are really uncertain about trying to stay in academia you may find that the commitment, interest, and support of some funding agencies, colleagues, collaborators, supervisors, grant assessors, and/or mentors will fade or vanish. Why should they invest scarce time or resources in you if you may disappear soon? You may then no longer have the option of staying.

Finally don't let uncertainty and anxiety about the future spoil your enjoyment of the present.
Doing good science should be a fun and is a privilege. Try and enjoy it, even if you may not get to do it in the long term.

I welcome discussion. It would be particularly good to hear some first or second-hand experiences of people who have made the transition from academia to industry.

Pseudogap in organic charge transfer salts

This post follows up on earlier posts including
Connecting the pseudogap to superconductivity in the organics

There is a nice paper
Pseudogap and Fermi arc in κ-type organic superconductors
by Jing Kang, Shun-Li Yu, Tao Xiang, and Jian-Xin Li

They use Cluster Perturbation Theory to study the Hubbard model on the anisotropic triangular lattice at half filling. They calculate the one-electron spectral function using clusters as large as 12 sites [embedded self-consistently in an infinite lattice].

The authors find three distinct phases: Mott insulator, Fermi liquid, and a pseudogap state with Fermi arcs. The latter occurs in between the two other phases.

The Figure below shows an intensity map of the spectral function at the Fermi energy for U=4t and t'=0.7t. This clearly shows a complete Fermi surface (with hot spots).

As U increases towards the Mott phase, U=5t one sees parts of the Fermi surface gap out leaving Fermi arcs. Note the cold spots [red region=low scattering=large spectral density] occur at the same place as the nodes in the superconducting gap.

This is quite reminiscent of the physics that occurs in the cuprates and the doped Hubbard model.