What simple plotting software would you recommend?

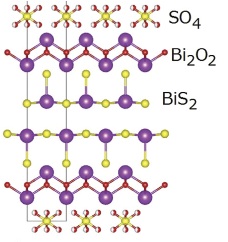
I have a second year undergraduate student working with me on a research project.
He needs to start producing some simple plots of one dimensional graphs, of publication quality. The plots will be of comparable complexity/simplicity to the figure below.

What freeware would you recommend?
There is a long list of options on Wikipedia.

The main criteria are

-free
-can be used on a PC and a Mac
-easy to learn and to use

The figure is from this paper.

Why large N is useful

In Hewson's book The Kondo problem to heavy fermions he devotes two whole chapters (7 and 8) to large N limits.

This is a powerful technique in quantum many-body theory and statistical physics. One expands the continuous symmetry of a specific model (e.g. from SU(2) to SU(N)) and then takes the limit of large N. If coupling constants are scaled appropriately the limit of infinite N can be solved analytically by a mean-field theory. One then considers corrections in powers of 1/N. This idea was first pursued for classical critical phenomena where the order parameter was an N-dimensional vector and the symmetry was O(N).

In the Kondo problem this is a particularly powerful and important technique for several reasons.

First, large N can be physically relevant. For example, cerium impurities have N=6 (N=14) when spin-orbit coupling is (not) taken into account.

Second, for any N there are exact results for thermodynamic properties from the Bethe ansatz solution. These provide something to benchmark approximate results from large N treatments.

Third, one can obtain results for dynamical and transport properties which cannot be calculated with the Bethe ansatz.

Fourth, because the analytics/mathematics is relatively simple in the slave boson and diagrammatic formulations one can gain some insight as to what is going on (perhaps).

Fifth, the large N limit and slave bosons can also be used to study lattice models such as Hubbard and Kondo lattice models.

Finally, it works!, giving results that are better both qualitatively and quantitatively than one might expect. For example, Bickers, Cox, and Wilkins used large N to give a comprehensive description of a whole range of experimental properties.

But, the slave boson mean-field theory is far from perfect, working best below the Kondo temperature. In particular, it produces an artifact: a finite temperature phase transition (Bose condensation) at a temperature comparable to the Kondo temperature.

Open questions about multi-band Hubbard models

There is an interesting review article
Magnetism and its microscopic origin in iron-based high-temperature superconductors
by Pengcheng Dai, Jiangping Hu, Elbio Dagotto

The authors highlight

• the diversity of materials and types of magnetic order in the parent compounds 
• just giving a theoretical description of the parent compounds is a challenge
• that these materials are in an intermediate coupling (moderately? correlated) regime where weak-coupling treatments are inadequate 
• there are local magnetic moments at room temperature, which is well above most of the magnetic ordering temperatures
• how poorly understood the multi-band Hubbard model is, even at half filling

The phase diagram below is based on Hartree-Fock theory (which surely is quite inadequate). J_H is the Hund's rule coupling. The "physical region" is probably the parameter regime of the pnictides.

I am interested to know how this diagram compares to DMFT (dynamical mean-field theory) and DMRG studies on ladders.

Culture and the graduate student

Culture is a set of assumptions that are accepted without question.
Culture determines what is right, valued, important, and normal.

At my church there are many graduate students who are not originally from Australia. Many understandably struggle with the dual challenge of postgraduate study and negotiating a foreign culture. Consequently, I got asked to run a workshop "Thriving or surviving in postgraduate research." It covered a wide range of topics including mental health, managing your supervisor, and publishing. Most of the material has appeared on this blog before.

A significant part of the time was spent by the participants completing this worksheet and then discussing their answers among themselves.
I think this is much more effective and less overwhelming than me just telling them what to do, which I fear may be what happens at the workshops run by the university Graduate School (30+ detailed powerpoint slides in 50 minutes?).

Much of it is just as relevant to Australian students but it seems that non-Westerners particularly struggle with asking for and getting help from authoritarian figures such as their supervisors.

What is Herzberg-Teller coupling?

Is it something to do with breakdown of the Born-Oppenheimer approximation?

In molecular spectroscopy you occasionally hear this term thrown around. Google scholar yields more than 3000 hits. But I have found its precise meaning and the relevant physics hard to pin down. Quantum mechanics in chemistry by Schatz and Ratner is an excellent book, but the discussion on page 204 did not help me. "Herzberg-Teller" never appears in Atkins' Molecular quantum mechanics.

So here is my limited understanding.
Herzberg and Teller wanted to understand why one observed certain vibronic (combined electronic and vibrational) transitions that were not expected, particularly some that were expected to be forbidden on symmetry grounds. "Intensity borrowing" occurred.
Herzberg and Teller pointed out that his could be understood if the dipole transition moment for the electronic transition depended on the nuclear co-ordinate associated with the vibration. In the Franck-Condon approximation one assumes that there is no such dependence.

There is a nice clear discussion of this in Section 2.2 of
Spectroscopic effects of conical intersections of molecular potential energy surfaces
by Domcke, Koppel, and Cederbaum

They start with a simple Hamiltonian involving two diabatic states coupled to two vibrational modes. The diabatic states, by definition, do not depend on the nuclear co-ordinates.

They show how in the adiabatic approximation [which I would equate with Born-Oppenheimer] one neglects the nuclear kinetic energy operator and diagonalises the Hamiltonian to produce adiabatic states. But, the diagonalisation matrix depends on the nuclear co-ordinates. Hence, the adiabatic eigenstates depend on the nuclear co-ordinates. In the crude adiabatic approximation one ignores this dependence.

The photoelectron and optical absorption spectra depend on calculated the dipole transition
elements between electronic eigenstates. These depend on the nuclear co-ordinates via the diagonalisation matrix. In Franck-Condon (FC) one ignores this dependence. This dependence is the origin of the Herzberg-Teller coupling.

The figure below, taken from the paper, shows spectra for a model calculation for the butatriene cation. The curves from top to bottom are for Franck-Condon approximation, adiabatic approximation, and the exact result. (Note: the vertical scales are different). Comparing the top two curves on can clearly see intensity borrowing for the high energy transitions. Comparing to the bottom curve shows the importance of non-adiabatic effects; these are amplified by the presence of a conical intersection in the model.

Hence, it should be stressed that Herzberg-Teller and "intensity borrowing" are NOT non-adiabatic effects, i.e. they do NOT represent a breakdown of Born-Oppenheimer. This point is also stressed by John Stanton in footnote 3 of his paper I discussed in an earlier post.

Fulde on the chemistry-physics divide

When dealing with electronic correlations in solids, one finds that they often resemble those in corresponding molecules or clusters. Hence one would expect quantum chemistry and solid-state theory to be two areas of research with many links and cross fertilization. Regrettably this is not the case. The two fields have diverged to such an extent that it is frequently difficult to find even a common language, something we hope will change in the future. In particular it has become clear that the various methods applied in chemistry and in solid-state theory are simply different approximations to the same set of cumulant equations.

Peter Fulde, Correlated electrons in quantum matter (World Scientific, 2012), pages 3-4.

Why you should love diabatic states

An earlier post gave a brief primer on diabatic states.

There is a nice review article
Diabatic Potential Energy Surfaces for Charge-Transfer Processes
V. Sidis

He has an interesting discussion of the historical renaissance of interest in and use of diabatic states in atomic scattering problems.

Agreeing on graduate student expectations

Previously I have posted about the importance of supervisors and students/staff discussing mutual expectations before starting to work together.

I was interested to learn that at the University of New England (Armidale, Australia) there is a very detailed form that graduate students must work through with their supervisor and then sign. It covers a wide range of topics including regular meetings, project timelines, co-authorship, intellectual property, plagiarism, office space, ....

I think if such an exercise is done diligently and sincerely it could prevent many problems that can and do occur.
Do you agree or disagree?

I learnt about this form while perusing the thick book, Surviving and Thriving in Postgraduate Research by Ray Cooksey and Gael McDonald.

Thermal expansion in heavy fermion compounds

Measuring the thermal expansion of a crystal sounds like a really boring measurement and not likely to yield anything of dramatic interest. This may be true for simple materials. However, for strongly correlated electron materials it reveals some interesting and poorly explained physics.

First, it is amazing that using fancy techniques based on capacitors one can measure changes in lattice constants of less than one part per million!

Second, there is some interesting thermodynamics that follows from the Maxwell relations. The isotropic thermal expansion is related to the variation in the entropy with pressure

Hence, in a Fermi liquid metal the thermal expansion versus temperature should have a linear temperature dependence at low temperatures.

Below, I show the temperature dependence of the thermal expansion (along two different crystal directions) for the heavy fermion compound CeRu2Si2, reported in a PRB article. The lower two curves are from the structural analogue LaRu2Si2 which does not have a contribution from 4f electrons.

The peak in the cerium compound is arguably associated with the formation of a coherent Fermi liquid below a coherence temperature of about 10 Kelvin. Below that temperature the thermal expansion is approximately linear in temperature.

How big is the effect? One way to quantify it is terms of the Gruneisen parameter [see Ashcroft and Mermin, page 493].

where T_i is the characteristic temperature scale of the entropy [here the Kondo or coherence temperature]. For heavy fermion compounds Gamma is two orders of magnitude larger than for elemental metals or the values of order unity, typically associated with phonons in simple crystals. This implies an extremely strong dependence of the characteristic temperature on volume. As far as I am aware there is no adequate theory of these large magnitudes.

There is a recent preprint which reports the temperature dependence of the thermal expansion in the iron pnictide KFe2As2 and relates it to a coherent-incoherent crossover like that discussed above.

Motivations for learning the reciprocal lattice

This semester I am teaching half of a solid state physics course at the level of Ashcroft and Mermin. This week I introduced crystal structures and started on the reciprocal lattice. I have taught this many times before, but this time I realised something basic that I have overlooked before.

In the past I motivated the reciprocal lattice as a way to understand how one determines crystal structures, i.e. one shines an external beam of waves (x-rays, electrons, or neutrons) on a crystal and one sees how their wavevector is changed by a reciprocal lattice vector of the crystal.
However, similar physics applies to electron waves within the crystal. They can also undergo Bragg diffraction. This is particularly relevant for band structures and understanding how band gaps open up at the zone boundaries.

In the past, I never mentioned the latter motivation when introducing the reciprocal lattice. It only came up much later when discussing band structures...

Not all citations are desirable

Surely, getting cited is always a good thing.
No, it depends who cites you and why.

In 2009 I was co-author of a paper in PNAS which has already attracted more than 40 citations. This might sound impressive to some. The problem is that none of the papers look like worth reading. Some represent the quackery that the PNAS paper is debunking.

What really got my attention though was the paper below published in an Elsevier journal. I urge you to start to read the paper and tell me what you think.

Nonlocal neurology: Beyond localization to holonomy
G.G. Globus and C.P. O’Carroll
Department of Psychiatry, College of Medicine,
University of California Irvine

Is this for real?
Would you recommend these psychiatrists to your loved ones?

Exact solution of the Kondo model

This week in the Kondo reading group we are working through chapter 6 of Hewson, entitled "Exact solutions and the Bethe Ansatz."

The exact solution [i.e. finding analytic equations for thermodynamic properties for a model Hamiltionian] by Andrei and Wiegmann in 1980 was a remarkable and unanticipated achievement. First, it showed that the "solution" of the Kondo problem in the 1970s via numerical renormalisation group and Fermi liquid approaches was correct. Second, it gave analytic formula for thermodynamic properties in weak and strong magnetic fields. Third, it gave an explicit form for the scaling function for the specific heat over the full temperature range.

On the more mathematical side it was of interest because it used Bethe ansatz techniques previously used for quite different one dimensional lattice models (Heisenberg, Hubbard, Bose gas with delta function repulsion, ice-type....). This may have also stimulated the connection of the Kondo problem to boundary conformal field theory pioneered by Affleck and Ludwig around 1990.

Calculation of the Wilson number was one impressive result which really helped convince people that the Bethe ansatz solution was correct. This dimensionless ratio connects the Kondo energy scale at high and low energies, as discussed in my earlier post summarising chapter 4.

Some important physics. The first figure below shows the impurity magnetic moment versus magnetic field at zero temperature. The second figure shows the temperature dependence (on a logarithmic scale) of the magnetic susceptibility.

First, it is worth remembering the amazing fact that everything is universal and there is only ONE energy scale, the Kondo temperature.

Second, note how slowly one approaches the high energy limit where the impurity spin is decoupled from the conduction electrons. This is due to logarithmic terms. Even when the temperature or field is several orders of magnitude larger than the Kondo temperaure the effective moment of the impurity is still of order only 90 per cent of its non-interacting value.

7 ingredients for a relatively smooth Ph.D

Why do most Ph.D's take longer than "expected"?
Why is the end often extremely stressful for students?

On the one hand there can be a multitude of reasons. However, I would contend that often some basic things are overlooked or neglected, leading to problems.

Some people have come up with things like "7 secrets of highly successful research students". These title is good marketing but not accurate of the content. The ideas are not "secret" and they don't lead to "high success," just "moderate" success [i.e. completion in a reasonable amount of time] and reduced stress.

The reworked version below is due to Rob Hyndman, a Professor of Computer Science at Monash University, on his nice blog Hyndsight

1. Meet reg­u­larly with your supervisor.
2. Write up your research ideas as you go.
3. Have real­is­tic research goals.
4. Beware of dis­trac­tions and other commitments.
5. Set reg­u­lar hours and take holidays.
6. Make full use of the avail­able help.
7. Per­se­vere.

Some of this may be "obvious" and "basic". But actually doing all seven consistently requires significant discipline. I think most students struggle (as I did) because they neglect at least one of these.

I first encountered these "7 keys" in a nice presentation from the UQ graduate school. They run a whole range of "candidature skills training" workshops for postgraduate students. The presentation slides are online, but appear to be only available to the UQ community.
These are good examples of the "available help" students need to "make full use of".

Deconstructing triplet-triplet annihilation

Tim Schmidt gave a nice chemistry seminar yesterday about recent work from his group aimed at improving the thermodynamic efficiency of photovoltaic cells using upconversion associated with triplet-triplet annihilation.
It has refreshing to hear a talk which focussed on trying to understand the underlying photophysics, rather than just device fabrication and efficiency. He even had some slides with Hamiltonians!

The underlying idea is illustrated in the figure below. Two sensitizer molecule (in this case porphyrins) absorbs "low energy" photons via a singlet state S1 which decays to a triplet T1 via intersystem crossing. These triplets then excite triplets on two neighbouring emitters (in this case rubrene). The two triplets then annihilate on a single rubrene to produce a high energy singlet which can then decay optically. These "high energy" photons are then absorbed by a tandem solar cell.

The photophysics which is not really that well understood concerns the dynamics and mechanism of triplet-triplet annihilation. It is the opposite of singlet fission [featured in this earlier post] which is discussed nicely in a recent review by Smith and Michl.

A fundamental and basic question concerning both singlet fission and triplet-triplet annihilation is
what is the relevant reaction co-ordinate?
e.g., is it a particular molecular vibrational co-ordinate?

A recent article by Zimmerman, Musgrave and Head-Gordon suggests the relevant co-ordinate is the relative motion of the two chromophores, and that there is a breakdown of the Born-Oppenheimer approximation associated with process.

Can academics be happy?

Brian Martin has an interesting article On being a happy academic that is worth reading.
He reviews recent research about happiness [contentment, well-being or satisfaction with life, not "jumping for joy"] in the context of university faculty members. He points out that many values and goals sought by academics [promotion, salary increases, international reputation] actually fail to provide long-term satisfaction. Unlike most jobs, academics actually have a lot of freedom as to how they spend their time. They have the option of being "counter-cultural" and focusing on things that may actually bring lasting satisfaction: understanding things, solving research problems, and building meaningful relationships.

Aside: Martin has an interesting career history. He did a Ph.D in theoretical physics and ended up as a Professor of Social Science at the University of Wollongong.
He has the courage to ask questions that most of us are afraid to ask (at least in public). For example, he has an interesting critique of the Excellence in Research Australia assessment exercise. Amongst other problems, Martin points out the confusion associated with counting grants as outputs rather than inputs. [I made a similar point in this post].

Different career stages require different CVs

I have been looking a lot of postdoc applications recently and noticed how some include a Curriculum Vitae with irrelevant material. This highlights the basic point that your CV should be tailored to your audience and the job you are applying for.

Teaching experience is not relevant to most postdocs. It is relevant to faculty positions. Also, once you have a Ph.D, high school or non-scientific work experience is not relevant. A model CV for applying for postdocs is on John Wilkins one page guides.

Those making the transition from academia to industry need a completely different. CV. I am told industry usually likes much shorter CVs. They are not interested in long publication lists [with impact factors!] but rather experience at problem solving, working in teams, giving presentations,....

Superconductivity in BiS2 layers

When I was in Delhi, Satyabrata Patnaik, introduced me to a fascinating new family of superconductors. He had just published a JACS
Bulk superconductivity in Bismuth Oxysulfide Bi₄O₄S₃
Shiva Kumar Singh, Anuj Kumar, Bhasker Gahtori, Gyaneshwar Sharma, Satyabrata Patnaik, and Veer P. S. Awana

Immediate questions are:

• is the superconductivity unconventional?
• are strong correlations important [crucial]?
• what is the simplest possible effective Hamiltonian?

On the latter, the following two PRBs are helpful

Minimal electronic models for superconducting BiS2 layers
Hidetomo Usui, Katsuhiro Suzuki, and Kazuhiko Kuroki

BiS2-based layered superconductor Bi4O4S3

Yoshikazu Mizuguchi, Hiroshi Fujihisa, Yoshito Gotoh, Katsuhiro Suzuki, Hidetomo Usui, Kazuhiko Kuroki, Satoshi Demura, Yoshihiko Takano, Hiroki Izawa, and Osuke Miura

Here is the layered crystal structure

Electronic structure calculations support the idea that the BiS2 is where the electronic action is. The SO4 sites are not all occupied, which leads to doping into the BiS2 layer. One can write Bi4O4 (SO4)1-x Bi2S4 where x is the occupancy of the SO4 site.
Hence, the superconductor Bi4O4S3 has x=0.5.

What is the simplest model for the electronic structure within the BiS2 layers?

Usui, Suzuki, and Kuroki consider a two-band and a four-band model. The latter has this band structure

The two-band model is obtained from the four-band model by "integrating" out the orbitals on the S atoms, leaving two p-type orbitals on the Bi atoms, with the hopping integrals shown below (and given values in Table II of the paper)

It is interesting that the hopping t and t', between nearest and next-nearest neighbours is comparable, possibly meaning frustration may play a significant role.
x=0 is a band insulator. The horizontal dashed lines correspond to x=0.25 and x=0.5 (the superconductor).

Within the two-band model, it looks like the system is a long way from a half- or quarter- filling band where strong correlations may matter. Also, the relevant p-orbitals are much more extended than the localised d-orbitals in Fe pnictide and Cu oxide based superconductors.

However, the four band model is in some sense close to "half filling". Then the system can be viewed as two coupled charge-transfer insulators. The hybridisation leading to the energy gap and "band insulator" for x=0 may actually be overwhelmed by large Hubbard interactions and/or Hund's rule couplings. 

It will be interesting to see how this subject develops....

How does the spin-statistics theorem apply in condensed matter?

The spin-statistics theorem is an important result in quantum field theory. It shows that particles with integer spin must be bosons and particles with half-integer spin must be fermions.

Confusion then arises in the quantum many-body theory of condensed matter because there are theories [and materials!] which involve quasi-particles which appear to violate this theorem. Here are some examples:

• Spinless fermions. These arise in one-dimensional models. For example, the transverse field Ising model.
• Schwinger bosons which are spinors (bosonic spinons). These arise in Sp(N) representations of frustrated quantum antiferromagnets. They were introduced by Read and Sachdev.
• Anyons. In two dimensions one can have quasi-particles which obey neither bose nor Fermi statistics.

How is this possible? Like a lot of inconsistencies, the answer is to look at the underlying assumptions required to prove the theorem. These include assuming:

1. The theory has a Lorentz invariant Lagrangian.
2. The vacuum is Lorentz invariant.
3. The particle is a localized excitation. Microscopically, it is not attached to a string or domain wall.
4. The particle is propagating, meaning that it has a finite, not infinite, mass.
5. The particle is a real excitation, meaning that states containing this particle have a positive definite norm.

I think three dimensions [and a non-interacting, i.e. quadratic Hamiltonian] may be other assumptions.

In condensed matter, one or more of the above assumptions may not hold. For example, 

• inclusion of a discrete lattice breaks Galilean invariance
• spontaneous symmetry breaking  
• topological order can lead to non-local excitations
• in one dimension spinless fermions may be non-local [e.g. associated with a domain wall]

Thanks to Ben Powell for reminding me of this question.

Why do you keep publishing the same paper?

It is the easiest thing to do.
You get an interesting new result [a new technique or a new system] and then you publish a paper.
Now, there is lots of "low-lying fruit".
There are a few loose ends to tie up and so your write another paper providing a bit more evidence the first one was correct.
Or you apply a slightly different technique or probe to your new system.
Or you apply your new technique to a slightly different system.

Sometimes this may be reasonable, or even important.
But, other times this recycling may just reflect our laziness, lack of originality, or succumbing to the pressure to add more lines to our CV.

This issue was first brought to my attention when I was a postdoc. A research fellow suggested to me that each person in the group basically had a single paper they were "republishing". This shocked me. I am not sure this was fair but I have not forgotten the concern.

Later, a colleague was evaluating Professor X and told me he thought that "every paper X wrote was the the same." On reflection, I think this was quite harsh. X had a developed a powerful technique that they had applied to a range of systems. The technique was not easy to use and often produced definitive results. In contrast, other scientists X was being compared to might publish on a more diverse range of subjects, but not produce definitive results. Like Galileo, I think the former is more valuable.

We need to consider whether we are vulnerable to such criticism, even if it may be unfair. Unfortunately, perceptions do matter.

But, we should also ask whether it would be better if we moved on to something else, or at least diversified. Perhaps we should leave others to lie up the loose ends or take the next steps. I suspect that is what great scientists do.

I welcome suggestions of critieria to help decide when "enough is enough".

How many decades do you need for a power law?

Discovering power laws is an important thing in physics.
Often people claim they have evidence for one.
My question is:

Over how many orders of magnitude must the data follow the apparent power law for you to believe it?

Often I read papers or hear speakers showing just one decade (or less!).
Is this convincing? Is it important?

Personally, I find that my prejudice is that I need to see at least 1.5 decades before I even take notice. Two decades is convincing and three or more is impressive.

What do other people think?

Some of the most important power laws are those associated with critical phenomena (and scaling). The most impressive experiments see thermodynamic quantities which depend on a power of the deviation from the critical temperature by many orders of magnitude. My favourite experiment involved superfluid helium on the space shuttle and observed scaling over 7 decades!

Distinguishing quantum and classical turbulence

Classical turbulence is hard enough to understand. How about turbulence in a quantum fluid such as superfluid helium?
Is there any difference?
There is a nice viewpoint Reconnecting to superfluid turbulence which is a commentary on the 2008 PRL Velocity Statistics Distinguish Quantum Turbulence from Classical Turbulence.
A key difference between the quantum and classical case concerns the reconnection of vortices.

Interplay of dynamical and spatial fluctuations near the Mott transition

There is a nice preprint The Crossover from a Bad Metal to a Frustrated Mott Insulator by Rajarshi Tiwari and Pinaki Majumdar

They study my favourite Hubbard model: the half-filled model on an anisotropic triangular lattice, within a new approximation scheme.

Basically, they start with a functional integral representation and ignore the dynamical fluctuations in the local magnetisation. One is then left with calculated the electronic spectrum for an inhomogeneous spin distribution and averaging then averaging over these with the relevant Boltzmann weights. This has the significant computational/technical advantage that the calculation is a classical Monte Carlo simulation.

Hence, it treats spatial spin fluctuations exactly while neglecting dynamical fluctuations. 

This is a nice study because it complements the approximation of dynamical mean-theory  (DMFT): it ignores spatial fluctuations but treats dynamical fluctuations exactly.

The calculation captures some of the important properties of the model: the Mott transition, a bad metal, and a possible pseudogap phase.

This shows how an anisotropic pseudogap can arise in the model due to short-range antiferromagnetic spin fluctuations (clearly shown in Figure 5 of the paper, reproduced below). 

However, as I would expect, this approximation cannot capture some of the key physics that DMFT does: the co-existence of Hubbard bands and a Fermi liquid. This difference is clearly seen in the optical conductivity calculated by the two different methods.

There must be some connection with old studies [motivated by the cuprates] of Schmalian, Pines, and Stojkovic, of electrons coupled to static spin fluctuations with finite-range correlations [see e.g. this PRB].  

This combined importance of both dynamical and spatial fluctuations highlights to me the importance of a recent study by Jure Kokalj and I, which treated them on the same footing by using the finite temperature Lanczos method on small lattices. 

Problems @ email.edu

Email continues to create problems for me and some of my colleagues. Here are a few things to consider and be diligent about.

Be circumspect about what you write. Assume any email you write may be forwarded, either intentionally or by mistake, to the "wrong" party.

Wait 24 hours. Don't hit the reply (or forward) key in a rush. This may lead to saying things you regret later.

Turn it off. Limit how many times a day you look at it. It can waste a lot of time and be a significant distraction. Do you really need email on your mobile phone?

Think about the informality of your style. Perhaps the formality of what you write should be in proportion to the seniority of (or your personal closeness to) the person you write to.

The amount of time you spent composing an email should be in proportion to its importance.

Don't use the reply option if the subject of your email is different to the message you are replying to. This is a lazy way to find someone's address, but just confuses or irritates the recipient.

Three years ago I wrote a similar post.

I welcome comments and war stories.

MIstakes happen

I was disappointed to find a mistake in one of the figures of my recent paper on hydrogen bonding. Fortunately, the mistake has no implications for the results in the paper. I just made a basic mistake when using Mathematica(!) to produce the figure. (Rather ironic and noteworthy given recent discussions on this blog about the dangers of Mathematica).

The upper two plots in Figure 2 of the paper should be replaced with those below.

The mistake was kindly pointed out to me by Sai Ramesh and Bijyalaxmi Athokpam during my recent visit to Bangalore. They found they could not reproduce the figure and were wondering why.

In hindsight, it is obvious that there is something wrong with the original plots. Consider the energy gap between the two adiabatic curves at the co-ordinate at which the diabatic curves cross. This energy is 2 times Delta, the off-diagonal matrix element which couples the two diabatic states. A major idea/assumption in the paper is that Delta decreases exponentially with increasing R, the donor-acceptor distance. However, in the original figure this gap does not vary with R! The new curves above clearly show this trend.

It is amazing to me that this basic point was missed by me, and by several colleagues and referees who read the paper. But I must take full responsibility.

What should be learn from this?

1. It does not matter how many times we check something, we can still make basic mistakes. The easiest person to fool is yourself.
Co-authors need to be particularly diligent in checking each others work.
A fresh set of eyes may reveal problems.
Trying to reproduce results from scratch is often a good check.

2. Just because something is published does not mean it is correct!
When we find something in a published paper that is not quite right, we should not assume it is correct.

Mistakes happen.