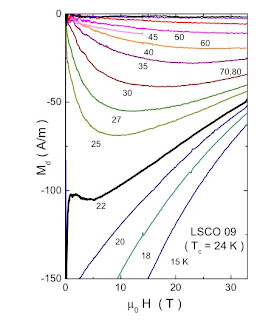
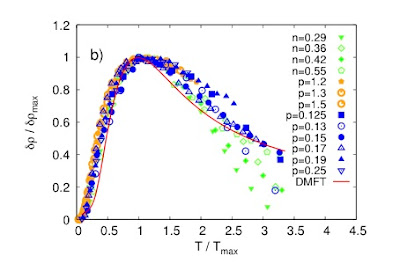
Can strongly correlated electrons save the planet II?
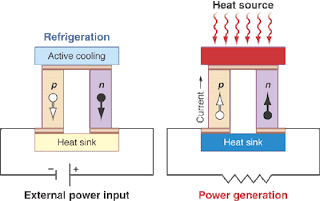
Several earlier posts discussed the thermoelectric effect in strongly correlated electron materials. The Seebeck coefficient S is a quantitative measure of the effect. At low temperatures it can be orders of magnitude larger than in elemental metals. The figure above illustrates how thermoelectric couples can be used to either perform refrigeration or generate electrical power from waste heat. It is taken from a nice Perspective in Science Smaller is Cooler by Brian Sales which reviews state of the art materials in 2002. The thermoelectric figure of merit , ZT is a dimensionless ratio which is a good measure of how useful a material will be in thermoelectric applications. sigma is the conductivity and kappa the thermal conductivity. Currently used materials such as Bi2Te3 [also a topological insulator!] have values of ZT ~1. If materials can be found with ZT~4 then thermoelectric refrigerators will be competitive with traditional compressor refrigerators, which are less r