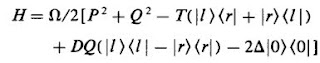At the Quantum Theory and Nature of Reality conference on Tuesday night there was an interesting panel discussion with George Ellis, Sir John Polkinghorne, and Sir Roger Penrose.
I was surprised and disappointed that Sir Roger Penrose re-iterated the same argument in his book The Emperors New Mind: quantum gravity, the collapse of the wavefunction, and consciousness must all be related. Furthermore, he stood by Hameroff's proposal that a particular type of microtubules are the component with quantum coherence. He mentioned how excited he was about unpublished experimental results of a Japanese group that claim to have measured an electrical resistance of one ohm for microtubules which is comparable to the resistance of the leads. [He seemed to be hinting this implied they were superconducting!].
Why am I so skeptical?
See the following:
The Penrose-Hameroff Orchestrated Objective-Reduction Proposal for Human Consciousness is Not Biologically Feasible, published in Physical Review E.
Is the Brain a Quantum Computer?, published in Cognitive Science. A physicist, psychologist, computer scientist, philosopher, and systems engineer say NO!
Insulating Behavior of λ-DNA on the Micron Scale, this PRL showed that claims that DNA could be conducting and even superconducting were experimental artifacts.
People tend to believe what they want to believe rather than what the evidence before them suggests they should believe. I call this Kauzmann's maxim and is articulated in his Reminiscences of a Life in Protein Chemistry.
Thursday, September 30, 2010
Wednesday, September 29, 2010
The emergence of locality
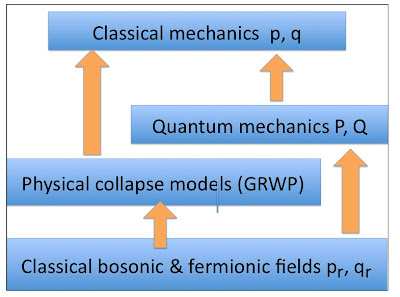
The following important question arises about Adler's proposal for the emergence of quantum field theory from an underlying statistical mechanics of bosonic and fermionic fields.
It appears to be a "hidden variables" theory. Shouldn't it obey Bell's theorem?
When asked this yesterday after my talk I said I thought that it does not because the "hidden variables" are fermionic. However, this is not the correct answer. It is because the underlying theory is nonlocal. Here is an extract (page 96 in the preprint version) of Adler's book:
It appears to be a "hidden variables" theory. Shouldn't it obey Bell's theorem?
When asked this yesterday after my talk I said I thought that it does not because the "hidden variables" are fermionic. However, this is not the correct answer. It is because the underlying theory is nonlocal. Here is an extract (page 96 in the preprint version) of Adler's book:
we note that there is a natural hierarchy of matrix structures leading from the underlying trace dynamics, to the emergent effective complex quantum field theory, to the classical limit. In the underlying theory, the matrices xr are of completely general structure.
No commutation properties of the xr are assumed at the trace dynamics level, and since all degrees of freedom communicate with one another, the dynamics is completely nonlocal. (As a consequence of this nonlocality, the Bell theorem arguments against local hidden variables do not apply to trace dynamics.)
In the effective quantum theory, the xr are still matrices, but with a restricted structure that obeys the canonical commutator/anticommutator algebra.
Thus, locality is an emergent property of the effective theory, even though it is not a property of the underlying trace dynamics. Finally, in the limit in which the matrices xr are dominated by their c-number or classical parts, the effective quantum field dynamics becomes an effective classical dynamics.
Thus, both classical mechanics and quantum mechanics are subsumed in the more general trace dynamics, as reflected in the following hierarchy of matrix structures, corresponding to increasing specialization:
general → canonical quantum → c-number, classical.
The indeterminacy characteristic of quantum mechanics appears only at the middle level of this hierarchy of matrix structures. At the bottom or trace dynamics level, there is no indeterminacy (at least in principle, given the initial conditions) because no dynamical information has been discarded, while at the top or classical level, quantum indeterminacies are masked by large system size.
A smart bird brain
Today Simon Benjamin (Oxford) gave a really nice talk, Will we succeed in creating entanglement in macroscopic quantum systems? Can it exist in living systems?
Specifically, Simon focused on recent theoretical work relating to the fascinating question of how migratory birds navigate (discussed in a previous post).
Specifically, they did a detailed analysis of decoherence and entanglement in the radical pair model for magnetoreception (where the small magnetic field of the earth causes a different decay rate for singlet and triplet channels). One thing I learnt is that a key to making this model work is that the different spins experience a different spin anisotropy associated with the hyperfine interaction. (How can we justify this asymmetry?)
Do living systems already harness quantum mechanics in a "non-trivial" way?
How do we define "non-trivial"? A good criteria is whether biologists and chemists need quantum physicists to understand the phenomena of interest?
Specifically, they did a detailed analysis of decoherence and entanglement in the radical pair model for magnetoreception (where the small magnetic field of the earth causes a different decay rate for singlet and triplet channels). One thing I learnt is that a key to making this model work is that the different spins experience a different spin anisotropy associated with the hyperfine interaction. (How can we justify this asymmetry?)
Recent experiments showed that a very weak oscillatory magnetic field resonant with the electron Larmor frequency will stop the compass working.
unknown rate = 10^4 per sec to disrupt compass
The Oxford group estimated the decoherence time must be shorter than 100 microsec.
This may seem long since N @ C60 has a decoherence time of 80 microsec.
An open question is the biomolecular justification for the radical pair model and whether the spins need to be in a protected environment.
A candidate molecule cryptochrome have too many nuclear spins.
This is fascinating. Is it "non-trivial"? Well it is worth noting that
1. all the theoretical machinery used was more than 50 years old [i.e. preceded quantum information theory].
2. the entanglement involved involves two electrons and just two molecules and so is not "macroscopic"
A question was ask about whether the bird had evolved to develop this feature because it has a survival advantage. It is important to remember that not every function of an animal has been optimised by evolution, as discussed here.
A question was ask about whether the bird had evolved to develop this feature because it has a survival advantage. It is important to remember that not every function of an animal has been optimised by evolution, as discussed here.
Emergence and quantum theory
I just finished preparing my talk, Is emergence the nature of physical reality? for the Polkinghorne birthday conference. I have really enjoyed thinking about these issues and learnt a lot.
Monday, September 27, 2010
Information is a bad word
John Bell had a list of BAD works which have been mentioned several times today. In his article, Against Measurement, Bell said:
His D. Phil thesis in on the arxiv and is forthcoming as an OUP book, Quantum Information Theory and the Foundations of Quantum Mechanics.
I found the talk refreshing.
One person at the conference who has a different view is Vlatko Vedral, who just wrote a popular book, Decoding Reality: The Universe as Quantum Information. An interview in the Observer has the title, I'd like to explain the Origin of God.
I will abstain from comment and leave you to form your own opinion.
"For the good books known to me are not much concerned with physical precision. This is clear already from their vocabulary. Here are some words which, however legitimate and necessary in application, have no place in a formulation with any pretension to physical precision: system, apparatus, environment, microscopic, macroscopic, reversible, irreversible, observable, information, measurement. .... On this list of bad words from good books, the worst of all is 'measurement'."Chris Timpson (Oxford, Philosophy) gave a nice talk, Information: more trouble than its worth, where he roundly and rightly criticised approaches to solving the quantum measurement problem which claim it is just an issue of "information" and the quantum theory is "just about information".
His D. Phil thesis in on the arxiv and is forthcoming as an OUP book, Quantum Information Theory and the Foundations of Quantum Mechanics.
I found the talk refreshing.
One person at the conference who has a different view is Vlatko Vedral, who just wrote a popular book, Decoding Reality: The Universe as Quantum Information. An interview in the Observer has the title, I'd like to explain the Origin of God.
I will abstain from comment and leave you to form your own opinion.
A divergent point of view
I am now in Oxford for the Quantum Theory and Nature of Reality conference. In their white paper, Andreas Doring and Chris Isham write about Quantum Field Theory (QFT):
Notwithstanding the success of standard quantum theory in atomic, molecular and solid-state physics, there are good reasons for wanting to see beyond it. For example, relativistic QFT is still plagued with ultra-violet divergences, and even free fields encounter the self-energy problem. No matter how sophisticated the renormalisation procedure that is adopted, the fact remains that relativistic QFT is fundamentally flawed.
This ultra-violet problem is clearly linked to the continuum model for space and time...
I may be missing their point but I would like to offer a possible alternative perspective: the divergence problems with renormalisation are not a problem with QFT but rather merely reflect the stratified nature of reality (discussed in my white paper) i.e. there is a hierarchy of energy scales and with each there emerge new interactions and phenomena which are described by some effective theory). In quantum field theory one is always working with some effective Hamiltonian/Lagrangian which describes interactions at some energy scale. To prevent divergences associated with renormalisation one introduces some high energy (or short wavelength) cutoff. This just reflects that there is other physics which becomes relevant at higher energies and is not explicitly contained with the starting Lagrangian or in its renormalised version which emerges from high energy processes.
I would argue that these problems are not unique to quantum field theory. They are also present for the renormalisation theory of classical phase transitions. In that case they also just reflect the
Sunday, September 26, 2010
Deconstructing hydrogen bonds
Hydrogen bonds are incredibly important for understanding the properties of water and for a wide range of biomolecular structures and processes. Without them you would be dead!
Unlike most chemical bonds, hydrogen bonds can range significantly in length, strength, and vibrational frequency. The graph below from a Science paper The Quantum structure of the Intermolecular Proton bond.
shows how the vibrational frequency of an asymmetric A-O-H...O-B bond varies with the proton affinity difference between A and B. Note the substantial softening as things get more symmetrical.
The figure below from another paper shows how the frequency softening is correlated with the bond length.
I am particularly interested in this because I want to know these effects depend on
- breakdown of the Born-Oppenheimer approximation
- the partially covalent character of hydrogen bonds
and whether a simple model Hamiltonian with two diabatic states and one vibrational mode treated exactly (see this earlier post) can capture the essential details and the trends above.
Saturday, September 25, 2010
Too fat to walk
Why are animals the size they are?
Are giant ants physically possible? No.
This comes up in the banter in an episode The Wheaton Recurrence of The Big Bang Theory which I watched on the Brisbane-Singapore flight last night.
A post on The Big Blog Theory discusses the science. Basically, weight increases with volume while function increases with area.
Are giant ants physically possible? No.
This comes up in the banter in an episode The Wheaton Recurrence of The Big Bang Theory which I watched on the Brisbane-Singapore flight last night.
A post on The Big Blog Theory discusses the science. Basically, weight increases with volume while function increases with area.
Astute observers (esp. Australians may recognize the cliffs in the photo above as the coastline near Bondi Beach). The sculpture above is described here.
Friday, September 24, 2010
Do you really think the cat is really dead?
I just re-read most of Tony Leggett's review article, Testing the limits of quantum mechanics: motivation, state of play, prospects. He considers that different interpretations of quantum mechanics broadly fall into three classes.
1. The statistical interpretration.
This claims that quantum state amplitudes (i.e. wavefunctions) have no reality but are merely a calculational device to calculate the probabilities of the outcome of measurements. Questions about whether a cat is dead or alive before it is measured are
ruled to be not "meaningful." The most "trenchant" advocate is Leslie Ballentine.
2. The orthodox interpretation.
QM amplitudes are "real" at the microscopic level but effectively not real (or at least not relevant) at the macroscopic level. This is claimed to be because of decoherence one can "For All Practical Purposes" (FAPP) never observe quantum interference between macroscopically distinct states.
1. The statistical interpretration.
This claims that quantum state amplitudes (i.e. wavefunctions) have no reality but are merely a calculational device to calculate the probabilities of the outcome of measurements. Questions about whether a cat is dead or alive before it is measured are
ruled to be not "meaningful." The most "trenchant" advocate is Leslie Ballentine.
2. The orthodox interpretation.
QM amplitudes are "real" at the microscopic level but effectively not real (or at least not relevant) at the macroscopic level. This is claimed to be because of decoherence one can "For All Practical Purposes" (FAPP) never observe quantum interference between macroscopically distinct states.
3. The many-worlds interpretation.
Quantum states do exist in "reality". But when I think I measure the cat is dead this is actually an "illusion" because the alive state is "equally real." I am just unaware of it.
Leggett's view is that 1. and 3. are largely hermeneutical gymnastics that allow one to avoid discussing the problem. His agenda is to propose experimental tests of 2.
Thursday, September 23, 2010
Physics hubris?
There is an interesting piece on the New York Times web site which quotes numerous scientists slamming Bob Laughlin's recent article about climate change. I wish he would go back to doing regular science....
On a more positive note Laughlin has a worthwhile project that is digitising Conrad Herring's famous file card box.
On his website he also has all the cartoons from his wonderful book, The Emergent Universe.
On a more positive note Laughlin has a worthwhile project that is digitising Conrad Herring's famous file card box.
On his website he also has all the cartoons from his wonderful book, The Emergent Universe.
Wednesday, September 22, 2010
Emergence of Biomolecular function
- How can something become more "ordered" as the temperature increases?
- Are one-dimensional Ising-type models good for anything?
- How can you distinguish different models for a complex system?
- When and how do biomolecules exhibit collective effects?
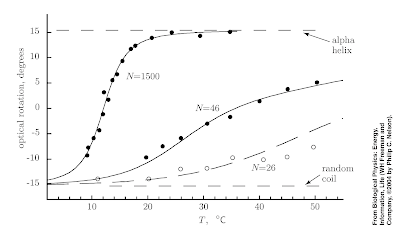
In Chapter 9 of Nelson's Biological Physics answers to these questions are illustrated by the Figure below which shows the temperature temperature of the fraction of a polypeptide chain that form an alpha-helix.
1. The fraction of the chain which forms alpha helices increases with increasing temperature. This is somewhat counter-intuitive. The reason it occurs is although the entropy of the chain decreases with increasing alpha helix content the entropy of the solvent decreases. Formation of alpha helices makes the solvent less ordered because formation of intra-chain hydrogen bonds mean there is less H-bonding of the solvent to the chain.
2. Yes. I remember solving the one-dimensional Ising model in a field when learning "advanced" statistical mechanics at the beginning of my Ph.D. This was considered a warmup for the two-dimensional model and to introduce the transfer matrix technique. However, it turns out the model also describes a one-dimensional polymer chain with an energy cost gamma to backfolding. The "magnetisation" versus temperature curve corresponds to the solid curve in the figure above.
3. Nelson points out that the data for N=1500 is adequately described by the "Ising model" with a large range of gamma values. Hence, the fact that one can fit the models predictions to the data hardly proves the model is correct. But then he goes on to show that the dependence on the chain length is quite sensitive to the gamma value. Indeed the data for all three N values can be described by a model with five parameters. Furthermore, a non-zero value of gamma is crucial showing the importance of interactions and co-operative effects.
4. The fact that the sharpness of the random coil-helix coil transition is sharp for large N is a signature of co-operativity (collective behaviour). Smaller polypeptide chains do not exhibit such a sharp transition. Why does this matter for biomolecular functionality? Because functionality involves turning on and off properties. Hence, biomolecules can undergo significant conformational change in response to a small change in ion concentration, temperature, or local environment.
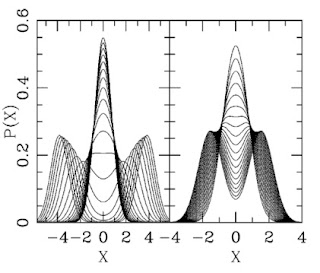
Border control
This cartoon appears in “Decoherence and the Transition from Quantum to Classical – Revisited,” quant-ph/0306072 by W. Zurek [This is a “remodeling” of his influential 1991 Physics Today article].
Tuesday, September 21, 2010
Effective Hamiltonian for atom-surface interactions
Why and how do atoms chemically bond to surfaces?
This can be described by the Newns-Anderson model Hamiltonian.
A nice brief overview is the chapter on Hetergeneous Catalysis by Bligaard and Norskov, from the book Chemical Bonding at Surfaces and Interfaces.
This can be described by the Newns-Anderson model Hamiltonian.
A nice brief overview is the chapter on Hetergeneous Catalysis by Bligaard and Norskov, from the book Chemical Bonding at Surfaces and Interfaces.
Monday, September 20, 2010
Stretching our understanding of biomolecules
Cooperative transitions in macromolecules is the title of Chapter 9 in Biological Physics by Phil Nelson and this weeks reading for BIPH3001.
Biological question: Why aren’t proteins constantly disrupted by thermal fluctuations?
The cartoons in cell biology books show proteins snapping crisply between definite conformations, as they carry out their jobs. Can a floppy chain of residues really behave in this way?
Physical idea: Cooperativity sharpens the transitions of macromolecules and their assemblies.
As usual the section headings are informative.
9.1 Elasticity models of polymers
9.1.1 Why physics works (when it does work)
Here he gets to the heart of emergence and effective Hamiltonians introducing the important idea.
9.1.3 Polymers resist stretching with an entropic force
9.2 Stretching single macromolecules
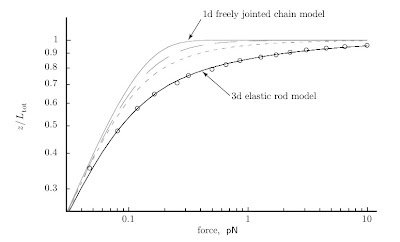
9.2.1 The force–extension curve can be measured for single DNA molecules
The lines are the predictions of a simple model for the length of a polymer versus the force applied to stretch it. The circles are actual experimental data for DNA molecules.
9.2.2 A simple two-state system qualitatively explains DNA stretching at low force
more later.....
Biological question: Why aren’t proteins constantly disrupted by thermal fluctuations?
The cartoons in cell biology books show proteins snapping crisply between definite conformations, as they carry out their jobs. Can a floppy chain of residues really behave in this way?
Physical idea: Cooperativity sharpens the transitions of macromolecules and their assemblies.
As usual the section headings are informative.
9.1 Elasticity models of polymers
9.1.1 Why physics works (when it does work)
Here he gets to the heart of emergence and effective Hamiltonians introducing the important idea.
When we study a system with a large number of locally interacting, identical constituents, on a far bigger scale than the size of the constituents, then we reap a huge simplification: Just a few effective degrees of freedom describe the system’s behavior, with just a few phenomenological parameters.9.1.2 Four phenomenological parameters characterize the elasticity of a long, thin rod
9.1.3 Polymers resist stretching with an entropic force
9.2 Stretching single macromolecules
9.2.1 The force–extension curve can be measured for single DNA molecules
The lines are the predictions of a simple model for the length of a polymer versus the force applied to stretch it. The circles are actual experimental data for DNA molecules.
9.2.2 A simple two-state system qualitatively explains DNA stretching at low force
Who should be a co-author?
Everyone should make sure they are familiar with the American Physical Society's guidelines:
This article on physics postdocs perceptions of the issue is worth reading.
When in doubt ask your supervisor to discuss these issues.
Authorship should be limited to those who have made a significant contribution to the concept, design, execution or interpretation of the research study. All those who have made significant contributions should be offered the opportunity to be listed as authors. Other individuals who have contributed to the study should be acknowledged, but not identified as authors.Some reasons why someone should not be a co-author:
- All they did was obtain the funding for the project.
- Their only contribution is that they are the official supervisor of a student who is a co-author.
- They have not read the paper!
- Their only contribution is that their status in the field may help get the paper published.
- They are not confident the results are valid. In particular, they cannot claim the future option of saying, "Well I didn't work on that part. I always had my doubts about that part..."
This article on physics postdocs perceptions of the issue is worth reading.
When in doubt ask your supervisor to discuss these issues.
Saturday, September 18, 2010
Frustrated about defects
I would have thought that the solid state of something as "simple" as elemental boron would be both well understood and "boring". However, that is not the case. There is a beautiful paper from Giulia Galli's group. A few things I learnt about beta-rhombohedral boron.
- Boron tends to form three centre two electron bonds.
- It contains 320 atoms per hexagonal unit cell! 6 out of 20 crystallographic sites are only partially occupied.
- The defect formation energy is negative leading to macroscopic numbers of intrinsic defects.
- The occupancy of the defects can be described in terms of a generalised Ising spin model on an expanded Kagome lattice.
- This Ising model describes the geometrical frustration associated with the defects, and the residual entropy present at zero temperature.
I am curious as to whether there is any need to take into account quantum fluctuations.
Friday, September 17, 2010
Theoretical physics on prime time TV
The Big Bang Theory now has 12 million viewers!
In the first episode when Penny and Sheldon first met he showed off his whiteboard. Which he said had a spoof of the Born-Oppenheimer approximation at the bottom (video)
[I could not read it. Anyone know what it is?].
I also read an interview with UCLA physics professor David Saltzburg who is consultant to the show. He now writes a blog The Big Blog Theory which explains the science which features in each show.
Thursday, September 16, 2010
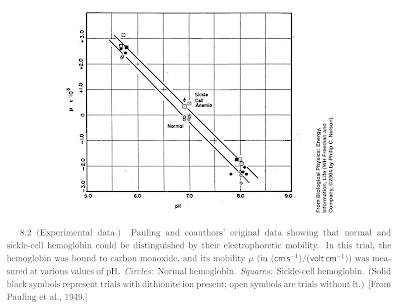
The origin of molecular medicine
The data in the Figure above changed the face of medical research.
It showed for the first time that disease can have a molecular basis.
It was another great scientific achievement and bold discovery of Linus Pauling.
The Figure is discussed in chapter 8 of Nelson's Biological Physics: Energy, Information, Life. He states:
In a historic discovery, Linus Pauling and coauthors showed in 1949 that the red blood cells of sickle-cell patients contained a defective form of hemoglobin. Today we know that the defect lies in parts of hemoglobin called the β-globin chains, which differ from normal β-globin by the substitution of a single amino acid, from glutamic acid to valine in position six. This tiny change (β-globin has 146 amino acids in all) is enough to create a sticky (hydrophobic) patch on the molecular surface. The mutant molecules clump together, forming a solid fiber of fourteen interwound helical strands inside the red cell and giving it the sickle shape for which the disease is named. The deformed red cells in turn get stuck in capillaries, then damaged, and destroyed by the body, with the net effect of creating pain and anemia.
In 1949, the sequence of β-globin was unknown. Nevertheless, Pauling and coauthors pinpointed the source of the disease in a single molecule. They reasoned that a slight chemical modification to hemoglobin could make a correspondingly small change in its titration curve, if the differing amino acids had different dissociation constants.
A nice article about the history is by William Eaton.
The Oxford questions on quantum reality
I am looking forward to the conference Quantum Physics and the Nature of Reality beginning in 10 days in Oxford. It is in honour of the 80th Birthday of Sir John Polkinghorne.
The following have been proposed as The Oxford Questions which will be refined at the conference.
The following have been proposed as The Oxford Questions which will be refined at the conference.
- 1. Are quantum states fact or knowledge, and how would you distinguish? (Stig Stenholm)
- 2. What does quantum physics teach us about the concept of physical reality? (Richard Healey)
- 3. What statements about quantum reality could be experimentally evaluated?
- 4. Are complex quantum systems best described in terms of constituents or relationships?
- 5. How does macroscopic classical behaviour emerge from microscopic quantum properties? (Gerard Milburn)
- 6. Why isn't nature more non-local? (Sandu Popescu)
- 7. Is realism compatible with true randomness? (Nicolas Gisin)
- 8. Is emergence the nature of physical reality? (Ross McKenzie)
- 9. Who (or what) is the quantum mechanical observer? (Alexei Grinbaum)
- 10. Can quantum theory and special relativity peacefully coexist? (M. Seevinck)
- 11. Quantum theory: science, mathematical metaphysics or mysticism? (Nicolaas Landsman)
- 12. What is conception of time best coheres with quantum formalism? (Daniel Greenberger)
- 13. Can strict irreversibility resolve the quantum measurement problem? (Andrew Steane)
- 14. What does physical reality tell us about the limitations of quantum theory and the possibility of going beyond it? (Andreas Doering & Chris Isham)
Tuesday, September 14, 2010
A new spin liquid material?
Many previous posts have discussed the Heisenberg model on the anisotropic triangular lattice which is relevant to the Mott insulating phase in a range of organic charge transfer salts and Cs2CuCl4.
A recent paper suggested that CuNCN is also described by this model, based on DFT based [GGA + U] calculations for the measured crystal structure. They found J1/J2 ~ 0.8 meaning the system could have a spin liquid ground state.
I found this quite exciting.
However, last year some of the same authors suggested a different point of view here, based on a hypothetical crystal structure. I do not follow the arguments in the second paper. Experimentally they do not observe magnetic moments and that motivates looking at alternative crystal structures without antiferromagnetic interactions [at the Hartree-Fock level].
But a non-magnetic ground state is just what you expect for the relevant Heisenberg model in the parameter regime of the first paper.
I think the material and these important questions warrant further study.
Monday, September 13, 2010
Arcs or pockets in the pseudogap state?
An outstanding question concerning the underdoped cuprate superconductors [pseudogap state] concerns the true nature of their Fermi surface which appear in STM and ARPES experiments as a set of disconnected arcs. Theoretical models have proposed two distinct possibilities:
(1) each arc is the observable part of a partially-hidden closed pocket, and
(2) each arc is open, truncated at its apparent ends.
We show that measurements of the variation of the interlayer resistance with the direction of a magnetic field parallel to the layers can qualitatively distinguish closed pockets from open arcs.
The first figure below shows the weak angular dependence of the field dependence of the interlayer magnetoresistance for the case of Fermi surface pockets.
The second figure shows the strong angular dependence of the case of arcs.

The difference between the two cases arises because the field can be oriented such that all electrons on arcs encounter a large Lorentz force and resulting magnetoresistance whereas some electrons on pockets escape the effect by moving parallel to the field.
Saturday, September 11, 2010
Broken symmetry, broken heart
A week ago, we had a very interesting Physics department colloquium by Marcelo Gleiser about his recent book, A Tear at the Edge of Creation: A Radical New Vision for Life in an Imperfect Cosmos.
He discussed his growing disillusion with string theory and the search for a "theory of everything" which is based on the predominance of symmetry. He gave important examples of symmetry breaking in nature including CP violation in the electro-weak interactions [which because of the CPT theorem implies time reversal invariance] and the unique chirality of amino acids in proteins.
Although it was a nice talk I thought it was all a bit sad to see someone who had become so enamoured with the propaganda of the reductionism in the high-energy physics community that it was painful when doubts emerged. Most of the points Gleiser was making seem to me to have been made long ago (in a more constructive sense) by Anderson in his 1972 "More is Different" article in Science, and more passionately and more recently by Laughlin in A Different Universe.
He discussed his growing disillusion with string theory and the search for a "theory of everything" which is based on the predominance of symmetry. He gave important examples of symmetry breaking in nature including CP violation in the electro-weak interactions [which because of the CPT theorem implies time reversal invariance] and the unique chirality of amino acids in proteins.
Although it was a nice talk I thought it was all a bit sad to see someone who had become so enamoured with the propaganda of the reductionism in the high-energy physics community that it was painful when doubts emerged. Most of the points Gleiser was making seem to me to have been made long ago (in a more constructive sense) by Anderson in his 1972 "More is Different" article in Science, and more passionately and more recently by Laughlin in A Different Universe.
Friday, September 10, 2010
Why do molecules bond to metal surfaces?
This week Elvis Shoko, Seth Olsen, and I read more of the beautiful review article, by Roald Hoffmann, A chemical and theoretical way to look at bonding on surfaces.
One of the key ideas I learnt was how chemical bonding between a metal surface and a molecule can have a completely different physical mechanism than between just molecules.
The left side shows how the interaction between two molecules due to the two filled highest orbitals is repulsive.
In contrast, similar interactions between a molecular orbital and a filled metal orbital can be attractive because once the metal-molecule interaction is strong enough to push the anti-bonding orbital above the Fermi energy, there can be charge transfer to unoccupied metal states.
The Figure above shows the energy of interaction as a function of the distance of the molecule from the surface. This also provides an understanding of the energy barrier to chemisorption of the molecule on the surface.
Thursday, September 9, 2010
When does Born-Oppenheimer actually break down II?
Today I gave a talk at the cake meeting about dynamical Jahn-Teller models.
Wednesday, September 8, 2010
What did Gell-Mann wish someone told him when he was 20?
Earlier this year there was a conference in Singapore celebrating the 8oth birthday of Murray Gell-Mann. He gave an interesting talk, Some Lessons from Sixty Years of Theorizing, which is a good read. Here are just a couple of extracts:
things I wish someone had explained to me around 60 years ago....
The one I should like to emphasize particularly has to do with the frequently encountered need to go against certain received ideas. Sometimes these ideas are taken for granted all over the world and sometimes they prevail only in some broad region or in certain institutions. Often they have a negative character and they amount to prohibitions of thinking along certain lines. Now we know that most challenges to scientific orthodoxy are wrong and many are crank. Now and then, however, the only way to make progress is to defy one of those prohibitions that are uncritically accepted without good reason....He goes on to give some good historical examples, e.g., opposition to continental drift at Caltech...
doubt and messiness are inevitable. We should tolerate them, even embrace them......
I suffered for many decades from the belief that when hesitating between alter- natives I had to choose the correct one. Lyova Okun once quoted to me advice he had received from an older colleague: “Publish your idea along with the objections to it.” I would now add “Publish the two contradictory ideas along with their consequences and choose later.” Apparently the messiness of the process is inevitable. Instead of suffering while trying to make it perfectly clean and neat, why not embrace the messiness and enjoy it?
The last point is an indirect endorsement of the method of multiple alternative hypotheses.
Tuesday, September 7, 2010
Entropic forces keep you alive
I really like chapter 7, "Entropic forces" in Nelson's Biological Physics: Energy, Information, and Life, the reading for this week in BIPH3001.
Biological question: What keeps cells full of fluid? How can a membrane push fluid against a pressure gradient?
Physical idea: Osmotic pressure is a simple example of an entropic force.
You can learn a lot just from reading the great section headings
7.2.1 Equilibrium osmotic pressure obeys the ideal gas law.
7.2.2 Osmotic pressure creates a depletion force between large molecules
7.3.1 Osmotic forces arise from the rectification of Brownian motion
7.3.2 Osmotic flow is quantitatively related to forced permeation
7.4.1 Electrostatic interactions are crucial for proper cell functioning
7.4.3 Charged surfaces are surrounded by neutralizing ion clouds
7.4.4 The repulsion of like-charged surfaces arises from compressing their ion clouds
7.4.5 Oppositely charged surfaces attract by counterion release
7.5.1 Liquid water contains a loose network of hydrogen bonds
7.5.2 The hydrogen-bond network affects the solubility of small molecules in water
7.5.3 Water generates an entropic attraction between nonpolar objects
Biological question: What keeps cells full of fluid? How can a membrane push fluid against a pressure gradient?
Physical idea: Osmotic pressure is a simple example of an entropic force.
You can learn a lot just from reading the great section headings
7.2.1 Equilibrium osmotic pressure obeys the ideal gas law.
7.2.2 Osmotic pressure creates a depletion force between large molecules
7.3.1 Osmotic forces arise from the rectification of Brownian motion
7.3.2 Osmotic flow is quantitatively related to forced permeation
7.4.1 Electrostatic interactions are crucial for proper cell functioning
7.4.3 Charged surfaces are surrounded by neutralizing ion clouds
7.4.4 The repulsion of like-charged surfaces arises from compressing their ion clouds
7.4.5 Oppositely charged surfaces attract by counterion release
7.5.1 Liquid water contains a loose network of hydrogen bonds
7.5.2 The hydrogen-bond network affects the solubility of small molecules in water
7.5.3 Water generates an entropic attraction between nonpolar objects
Writing IS hard work
Struggling to write your thesis or a paper or a research proposal? You are not alone. This morning I read the following account of one person's struggle.
The best-selling author John Grisham in an op-ed piece in the New York Times.
Writing was not a childhood dream of mine. I do not recall longing to write as a student. I wasn’t sure how to start. Over the following weeks I refined my plot outline and fleshed out my characters. One night I wrote “Chapter One” at the top of the first page of a legal pad; the novel ..... was finished three years later.
The book didn’t sell, and I stuck with my day job, defending criminals, preparing wills and deeds and contracts. Still, something about writing made me spend large hours of my free time at my desk. I had never worked so hard in my life, nor imagined that writing could be such an effort. It was more difficult than laying asphalt, and at times more frustrating than selling underwear. But it paid off. Eventually, I was able to leave the law and quit politics. Writing’s still the most difficult job I’ve ever had — but it’s worth it.Who wrote this?
The best-selling author John Grisham in an op-ed piece in the New York Times.
Monday, September 6, 2010
When does Born-Oppenheimer actually break down?
A nice model to discuss non-adiabatic effects, vibronic transitions, and the breakdown of the Born-Oppenheimer approximation is the two site Holstein model, where two coupled degenerate electronic states are each coupled to a vibrational model. The can be reduced to following Hamiltonian which is also sometimes called the E x beta Jahn-Teller problem.
This model breaks the inversion symmetry Q to -Q, but has a combined symmetry when this transformation is combined with mapping the "left" electronic state |l> to the "right" one |r>. (see the previous post about such combined symmetries). This allows one to make a unitary transformation due to Fulton-Gouterman that reduces the problem to two "vibrational" problems which can be solved as continued fractions. This is discussed by in a paper by Kongeter and Wagner who calculate the spectrum below of eigenstates.
p=+1 and -1 are the quantum numbers associated with the combined inversion symmetry.
They make much of the non-perturbative nature of the problem.
However, I wonder if the above spectrum can be largely be explained in terms of the Born-Oppenheimer approximation for the two adiabatic potentials
E+- = omega Q^2/2 +- sqrt{T^2 + (D Q)^2}
The widely spaced levels are on the upper potential energy surface.
The lower narrowly spaced levels include tunnel splitting of vibrational states in the double well potential which is the lower potential energy surface.
What did Escher know?
In the interesting physics colloquium that Marcelo Gleiser gave on friday at UQ he used the Escher print above to illustrate CP symmetry in a system which violates both C and P symmetry.
[C is charge conjugation and P is parity].
I found the image here.
Another example of breaking of a symmetry while conserving a combined symmetry concerns vibronic transitions in molecules. For molecules which have inversion symmetry selection rules suggest that electronic transitions that involve no change in parity should not be observed. However, they sometimes are because they are combined with a vibrational transition. Hence, vibronic [= vib(rational)-(elect)ronic] transitions. I think the first observed case of this may have been in benzene.
Saturday, September 4, 2010
Is emergence the nature of physical reality?
Yesterday I finished my White paper for the conference, "Quantum physics and the nature of reality," to be held in honour of the 80th Birthday of Sir John Polkinghorne, later this month in Oxford.
I welcome any comments on the paper. The abstract is below.
Is emergence the nature of physical reality?
The concept of emergence provides a unifying framework to both characterise and understand the nature of physical reality, which is intrinsically stratified. Emergence raises philosophical questions about what is fundamental, what is real, and the possible limits to our knowledge. Important emergent concepts, particularly predominant in condensed matter physics, are highlighted: spontaneous symmetry breaking, quasi-particles and effective interactions, universality and protectorates. Three alternative emergent perspectives on the quantum measurement problem are discussed. (i) The classical world emerges from the quantum world via decoherence. (ii) Quantum theory is not exact but emerges from the statistical mechanics of underlying classical bosonic and fermionic fields, and (iii) The discontinuity between the quantum and classical worlds is another example of the epistemological (and possibly ontological) barriers between different strata of reality. Addressing the merits and deficiencies of each of these three perspectives from both theoretical, experimental, and philosophical approaches appears to me important, realistic, and exciting.
I welcome any comments on the paper. The abstract is below.
Is emergence the nature of physical reality?
The concept of emergence provides a unifying framework to both characterise and understand the nature of physical reality, which is intrinsically stratified. Emergence raises philosophical questions about what is fundamental, what is real, and the possible limits to our knowledge. Important emergent concepts, particularly predominant in condensed matter physics, are highlighted: spontaneous symmetry breaking, quasi-particles and effective interactions, universality and protectorates. Three alternative emergent perspectives on the quantum measurement problem are discussed. (i) The classical world emerges from the quantum world via decoherence. (ii) Quantum theory is not exact but emerges from the statistical mechanics of underlying classical bosonic and fermionic fields, and (iii) The discontinuity between the quantum and classical worlds is another example of the epistemological (and possibly ontological) barriers between different strata of reality. Addressing the merits and deficiencies of each of these three perspectives from both theoretical, experimental, and philosophical approaches appears to me important, realistic, and exciting.
Friday, September 3, 2010
Theories of everything
"every decade or so, a grandiose theory comes along, bearing similar aspirations and often brandishing an ominous-sounding C-name. In the 1960s it was cybernetics. In the 1970s it was catastrophe theory. Then came chaos theory in the '80s and complexity theory in the '90s."
Steven Strogatz, Sync : the emerging science of spontaneous order
Steven Strogatz, Sync : the emerging science of spontaneous order
Thursday, September 2, 2010
Planck's constant is emergent
Where do the following come from?
Planck's constant.
Dirac's canonical quantisation. (Identification of the quantum commutator with classical Poisson brackets).
Locality of quantum field theory.
The Born rule and definite outcomes of quantum measurements.
Could they emerge from some underlying theory?
Here is a brief summary of some of the key ideas in Quantum theory as an emergent phenomonen, by Stephen L. Adler. Helpful introductions are the slides [hand-written viewgraphs!] from a talk Adler gave in 2006 (see the summary slide below) and a review of the book by Philip Pearle. [There is also a draft of the book on the arXiv].
This is an incredibly original and creative proposal.
The starting point are "classical" dynamical variables pr, qr which are NxN matrices. Some bosonic and others are fermionic. They all obey Hamilton's equations of motion for an unspecified Hamiltonian H.
Three quantities are conserved, H, the fermion number N, and the traceless anti-self adjoint matrix:
where the first term is the sum of commutators over bosonic variables and the second the sum over anti-commutators over fermionic variables.
Quantum theory is obtained by tracing over all the classical variables with respect to an canonical ensemble with three (matrix) Lagrange multipliers corresponding to the conserved quantities H, N, and C.
The expectation value of the diagonal elements of C are assumed to all have the same value, hbar!
An analogy of the equipartition theorem (which looks like a Ward identity from field theory) leads to dynamical equations for effective fields. To make these equations look like quantum field theory an assumption is now made about a hierarchy of length, energy, and "temperature" [Lagrange mulitiplier] scales, which cause the Trace dynamics to be dominated by C rather than H, the trace Hamiltonian. Adler suggests these scales may be Planck scales. What then emerges are the usual quantum dynamical equations and the Dirac correspondence of Poisson brackets and commutators.
The "classical" field C fluctuates about its average value. These fluctuations can be identified with corrections to locality in quantum field theory and with the noise terms which appear in "physical collapse" models [e.g., Continuous Spontaneous Localisation] of quantum theory.
This is very impressive!
So some questions I have:
Planck's constant.
Dirac's canonical quantisation. (Identification of the quantum commutator with classical Poisson brackets).
Locality of quantum field theory.
The Born rule and definite outcomes of quantum measurements.
Could they emerge from some underlying theory?
Here is a brief summary of some of the key ideas in Quantum theory as an emergent phenomonen, by Stephen L. Adler. Helpful introductions are the slides [hand-written viewgraphs!] from a talk Adler gave in 2006 (see the summary slide below) and a review of the book by Philip Pearle. [There is also a draft of the book on the arXiv].
This is an incredibly original and creative proposal.
The starting point are "classical" dynamical variables pr, qr which are NxN matrices. Some bosonic and others are fermionic. They all obey Hamilton's equations of motion for an unspecified Hamiltonian H.
Three quantities are conserved, H, the fermion number N, and the traceless anti-self adjoint matrix:
where the first term is the sum of commutators over bosonic variables and the second the sum over anti-commutators over fermionic variables.
Quantum theory is obtained by tracing over all the classical variables with respect to an canonical ensemble with three (matrix) Lagrange multipliers corresponding to the conserved quantities H, N, and C.
The expectation value of the diagonal elements of C are assumed to all have the same value, hbar!
An analogy of the equipartition theorem (which looks like a Ward identity from field theory) leads to dynamical equations for effective fields. To make these equations look like quantum field theory an assumption is now made about a hierarchy of length, energy, and "temperature" [Lagrange mulitiplier] scales, which cause the Trace dynamics to be dominated by C rather than H, the trace Hamiltonian. Adler suggests these scales may be Planck scales. What then emerges are the usual quantum dynamical equations and the Dirac correspondence of Poisson brackets and commutators.
The "classical" field C fluctuates about its average value. These fluctuations can be identified with corrections to locality in quantum field theory and with the noise terms which appear in "physical collapse" models [e.g., Continuous Spontaneous Localisation] of quantum theory.
This is very impressive!
So some questions I have:
- How is the theory falsifiable? On some energy/time/length scales the underlying fluctuating classical fields must be experimentally accessible. But, will we ever be able to distinguish them from background decoherence?
- Is the assumption that all the expectation values of C have a simple diagonal form some version of a maximum entropy principle?
- This seems to be a "hidden variable theory" but with bosonic and fermionic hidden variables. How does this allow one to get around Bell's inequalities?
- The discussion of the fluctuating C field focuses on the part that causes collapse. [Im K(t)]. However, won't causality and Kramers-Kronig mean that this will have a real part. This will cause dynamical shifts in the energy eigenvalues of the Schrodinger equation? This could be easier to measure experimentally than collapse/decoherence. [See for example a discussion of dynamical Stokes shifts in biomolecules due interaction with their environment].
Wednesday, September 1, 2010
Structure-property relations for NLO materials
Finding organic molecules with large nonlinear optical NLO polarisabilities is desirable for many applications. An important example is the imaging of biological cells using fluorescent protein chromophores.
These images based on two photon microscopy using fluorescent protein chromophores.
Understanding how the NLO properties are related to the structure of the molecules is a fundamental question that has attracted considerable attention. In particular the NLO polarisability of conjugated dyes has been correlated with the amount of bond length alternation.
Seth Olsen and I have just finished a paper Bond Alternation, Polarizability and Resonance Detuning in Methine Dyes which looks at these questions.
Even though the molecules of interest can have a complex chemical structure it is possible to establish structure-property relations.
This Figure shows how the bond length variations can be correlated with a single parameter which measures the deviation of the molecule from resonance. An important result in our paper is the definition of the reference bond lengths in an asymmetric dye.

The above Figure shows how the nonlinear polarisability beta varies with the deviations from resonance.
Subscribe to:
Comments (Atom)
A golden age for precision observational cosmology
Yin-Zhe Ma gave a nice physics colloquium at UQ last week, A Golden Age for Cosmology I learnt a lot. Too often, colloquia are too speciali...

-
This week Nobel Prizes will be announced. I have not done predictions since 2020 . This is a fun exercise. It is also good to reflect on w...
-
Is it something to do with breakdown of the Born-Oppenheimer approximation? In molecular spectroscopy you occasionally hear this term thro...
-
Nitrogen fluoride (NF) seems like a very simple molecule and you would think it would very well understood, particularly as it is small enou...