A nice model to discuss non-adiabatic effects, vibronic transitions, and the breakdown of the Born-Oppenheimer approximation is the two site Holstein model, where two coupled degenerate electronic states are each coupled to a vibrational model. The can be reduced to following Hamiltonian which is also sometimes called the E x beta Jahn-Teller problem.
This model breaks the inversion symmetry Q to -Q, but has a combined symmetry when this transformation is combined with mapping the "left" electronic state |l> to the "right" one |r>. (see the previous post about such combined symmetries). This allows one to make a unitary transformation due to Fulton-Gouterman that reduces the problem to two "vibrational" problems which can be solved as continued fractions. This is discussed by in a paper by Kongeter and Wagner who calculate the spectrum below of eigenstates.
p=+1 and -1 are the quantum numbers associated with the combined inversion symmetry.
They make much of the non-perturbative nature of the problem.
However, I wonder if the above spectrum can be largely be explained in terms of the Born-Oppenheimer approximation for the two adiabatic potentials
E+- = omega Q^2/2 +- sqrt{T^2 + (D Q)^2}
The widely spaced levels are on the upper potential energy surface.
The lower narrowly spaced levels include tunnel splitting of vibrational states in the double well potential which is the lower potential energy surface.
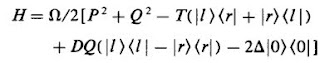





|0>=(|l>+|r>)/Sqrt(2)?
ReplyDeleteI take it P and Q are operators on the "nuclear" states... are D and T also operators or are they just numbers?
ReplyDelete|0> is the exciton ground state (just ignore it)
ReplyDeleteD and T are parameters
P and Q are the momemtum and position for the "nuclear" degrees of freedom.