The emergence of locality

The following important question arises about Adler's proposal for the emergence of quantum field theory from an underlying statistical mechanics of bosonic and fermionic fields.

It appears to be a "hidden variables" theory. Shouldn't it obey Bell's theorem?

When asked this yesterday after my talk I said I thought that it does not because the "hidden variables" are fermionic. However, this is not the correct answer. It is because the underlying theory is nonlocal. Here is an extract (page 96 in the preprint version) of Adler's book:

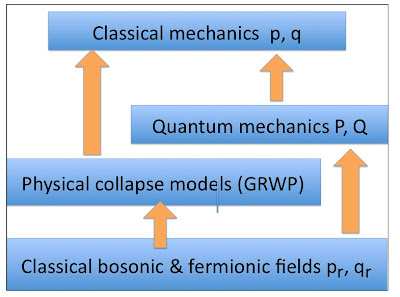
we note that there is a natural hierarchy of matrix structures leading from the underlying trace dynamics, to the emergent effective complex quantum field theory, to the classical limit. In the underlying theory, the matrices xr are of completely general structure.

No commutation properties of the xr are assumed at the trace dynamics level, and since all degrees of freedom communicate with one another, the dynamics is completely nonlocal. (As a consequence of this nonlocality, the Bell theorem arguments against local hidden variables do not apply to trace dynamics.)

In the effective quantum theory, the xr are still matrices, but with a restricted structure that obeys the canonical commutator/anticommutator algebra.

Thus, locality is an emergent property of the effective theory, even though it is not a property of the underlying trace dynamics. Finally, in the limit in which the matrices xr are dominated by their c-number or classical parts, the effective quantum field dynamics becomes an effective classical dynamics.

Thus, both classical mechanics and quantum mechanics are subsumed in the more general trace dynamics, as reflected in the following hierarchy of matrix structures, corresponding to increasing specialization:

general → canonical quantum → c-number, classical.

The indeterminacy characteristic of quantum mechanics appears only at the middle level of this hierarchy of matrix structures. At the bottom or trace dynamics level, there is no indeterminacy (at least in principle, given the initial conditions) because no dynamical information has been discarded, while at the top or classical level, quantum indeterminacies are masked by large system size.