Finding universal dimensionless ratios has proven key in understanding both elemental metals and strongly correlated Fermi liquids. Examples of important ratios include those associated with the names Sommerfeld-Wilson, Korringa, Lorenz, and Kadowaki-Woods. Here is another one...
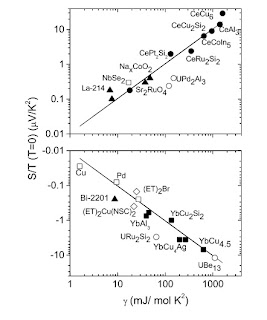
Today I read I nice article On the thermoelectricity of correlated electrons in the zero-temperature limit by Kamran Behnia, Didier Jaccard and Jacques Flouquet. The graph below shows evidence for a universal ratio for a wide range of materials. The ratio of the slope of the thermopower S(T) versus temperature to the specific heat coefficient gamma equals +/-1/eNA where NA is Avagadro's number and the sign depends on whether the charge transport is via electrons or holes.
Note the log-log scale which covers three decades.
This is the value of the ratio expected for a non-interacting fermion gas. It would be slightly different in Mott's formula for the thermopower with an energy dependent scattering rate [such subtleties are probably lost on the log-log scale].
A universal ratio for an Anderson impurity model was predicted by Houghton, Read, and Won [amongst others and discussed in Appendix E of Hewson's book on the Kondo effect].
A discussion of the temperature dependence of the thermopower for a DMFT (Dynamical-Mean-Field-Theory) treatment of the Hubbard model is here.




No comments:
Post a Comment