Two important signatures of a Fermi liquid metal are that at low temperatures (i.e. much less than the Fermi temperature) the specific heat is proportional to temperature and the magnetic susceptibility is independent of temperature. Both are proportional to the density of states at the Fermi energy and one can form a dimensionless ratio, the Sommerfeld-Wilson ratio:
R is unity for a non-interacting gas of fermions and is 2 for the impurity contribution in the single impurity Kondo model [Yamada proposed this highly non-trivial result and Wilson confirmed it with the numerical renormalization group].
An important property of heavy fermion metals both the specific heat and susceptibility are enhanced by approximately the same amount. This can be seen in the plot below, where the solid line corresponds to a Wilson ratio of unity.
The plot was first made in Barbara Jones 1985 Cornell Ph.D thesis.
This version is from Piers Coleman's review article Heavy Fermions: Electrons at the edge of Magnetism.More than 10 years ago I wrote a paper Wilson's ratio and the spin splitting of magnetic oscillations in quasi-two dimensional metals.
I failed to get it published because of subtle issues about vertex corrections. Nevertheless, the preprint still seems to be of some use to people. See for example, the recent preprint Direct observation of multiple spin zeroes in the underdoped high temperature superconductor YBa2Cu3O6+x
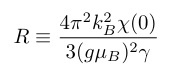



No comments:
Post a Comment