Ladder models provide a means to investigate in a controlled manner (e.g., via DMRG, bosonisation, and weak-coupling renormalisation group) physics which it is hoped may be related to what occurs in the two-dimensional limit.
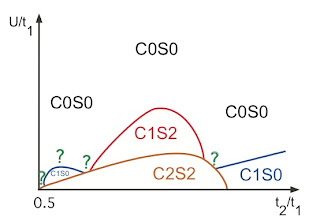
One can characterise different ground states on ladders by n and m, the number of gapless charge and spin modes, respectively. This leads to the notation CnSm and the following identifications.
C2S2 is the ladder analogue of Fermi liquid metal,
C1S0 is a superconductor,
C1S2 is a spin Bose metal,
C0S0 is a spin gapped Mott insulator,
C0S2 is a spin liquid Mott insulator.
Balents and Fisher used a weak-coupling RG approach to show that at half filling a two-leg ladder without frustration has a C0S0 ground state, which upon doping changes has a C0S0 ground state, which upon doping changes to C1S0 consistent with Anderson's RVB ideas.
Lai and Motrunich recently performed a weak-coupling renormalisation group analysis has been performed on the zig-zag ladder with longer-range Coulomb repulsion at half-filling. This is the ladder analogue of the Hubbard model that should describe organic charge transfer salts. The longer-range interaction stabilises the C2S2 phase and leads to a subtle competition between all the different phases listed above. Indeed it is interesting to compare their Figure 8
with the full two-dimensional lattice model.




No comments:
Post a Comment