Any rigorous theorem on quantum many-body systems is useful.
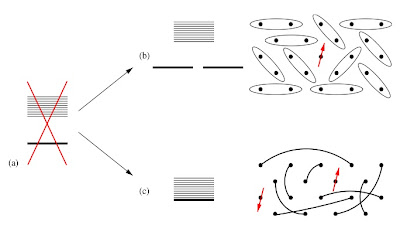
An important theorem for quantum spin systems was proven by Hastings. It is a generalization of the Lieb–Schultz–Mattis theorem to dimensions larger than one. It concerns spin-1/2 systems with one spin per unit cell on a two-dimensional lattice with periodic boundary conditions (on a torus). The theorem states that if there is no symmetry breaking then the ground state is separated from the first excited state by an energy gap that vanishes in the thermodynamic limit. Hence, under these specific conditions one cannot have a singlet ground state with a non-zero energy gap.
There is a nice discussion of the theorem in some lecture notes by Matthew Fisher, which contains the Figure below.




No comments:
Post a Comment