Phonons in organic molecular crystals.

In any crystal the elementary excitations of the lattice are phonons. The dispersion relation for these quasi-particles relates their energy and momentum. This dispersion relation determines thermodynamic properties such as the temperature dependence of the specific heat and plays a significant role in electron-phonon scattering and superconductivity in elemental superconductors. A nice introduction is in chapter 13 of Marder's excellent text. [The first two figures below are taken from there].

The dispersion relation is usually determined in at least one of three different ways.

1. The classical mechanics of balls and harmonic springs, representing atoms and chemical bonds, respectively. One introduces empirical parameters for the strengths of the bonds (spring constants).

2. First-principles electronic structure calculations, often based on density functional theory (DFT). This actually just determines the spring constants in the classical model.

3. Inelastic neutron scattering.

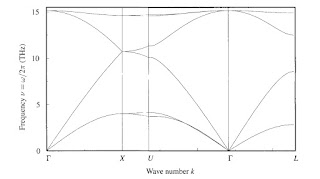
The figure below shows the dispersion relations for a diamond lattice using parameters relevant to silicon, using method 1. I find it impressive that this complexity is produced with only two parameters.

Furthermore, it produces most of the details seen in the dispersion determined by method 3. (Squares in the figure below.) which compare nicely with method 2. (solid lines below).

What about organic molecular crystals?
The following paper may be a benchmark.

Phonon dispersion in d8-naphthalene crystal at 6K 
I Natkaniec, E L Bokhenkov, B Dorner, J Kalus, G A Mackenzie, G S Pawley, U Schmelzer and E F Sheka

The authors note that method 3. is particulary challenging for three reasons.

• The difficulties in growing suitable single-crystal samples. 
• The high energy resolution necessary to observe the large number of dispersion curves (in principle there are 3NM modes, where N is the number of atoms per molecule and M is the number of molecules per unit cell). 
• The high momentum resolution necessary to investigate the small Brillouin zone (due to the large dimensions of the unit cell).

The figure below shows their experimental data for the dispersions. The solid lines are just guides to the eye.

The authors also compare their results to method 1. However, the results are not that impressive, partly because it is much harder to parameterise the intermolecular forces, which are a mixture of van der Waals and pi-pi stacking interactions. Hence, crystal structure prediction is a major challenge.

A recent paper uses method 2. and compares the results of three different DFT exchange-correlation functionals to the neutron scattering data above.
Ab initio phonon dispersion in crystalline naphthalene using van der Waals density functionals
Florian Brown-Altvater, Tonatiuh Rangel, and Jeffrey B. Neaton

What I would really like to see is calculations and data for spin-crossover compounds.