An important step in understanding any class of complex materials is to find/discover the simplest possible effective Hamiltonian that can be used to describe the main properties of interest (e.g. a phase diagram).
Doing this well is a non-trivial and subjective process. I am thinking about this because I am currently trying to figure out the appropriate Hamiltonian for spin-crossover compounds.
Here are some key elements of the process.
"Simplest possible" means having the fewest possible degrees of freedom and parameters.
1. What are the key degrees of freedom (molecular orbitals, vibrations, spins, ...)?
2. What are the key interactions and the associated Hamiltonian?
3. What approximation scheme can be used to calculate properties of the many-body Hamiltonian (ground state, thermodynamics, electronic, magnetic, ...)?
4. How do the calculated properties compare to experiment?
5. Can we estimate the values of the Hamiltonian parameters from the comparison of the calculated properties with experiments?
6. Can we estimate the values of the Hamiltonian parameters from ab initio electronic structure methods, such as those based on density functional theory (DFT)?
Inevitably, things do not work out perfectly, sometimes qualitatively and always somewhat quantitatively. Then one has to face the difficult task of deciding what the problem is and what the next step is. There are several options.
A. There are some missing degrees of freedom in the original Hamiltonian.
B. There are some missing interactions.
C. The approximation scheme used to calculate properties was not reliable enough.
D. There is a problem with the experiments.
E. This is really the best one can hope to do and you should move on to other problems. i.e, know when to quit and face the law of diminishing returns.
This plethora of options is why falsifiability is so hard in the theory of strongly correlated electron materials. But, it does not mean we should give up on it.
The flow diagram below is one way of looking at the process. Some people like the picture. Others do not. As usual, real science is not quite so algorithmic.
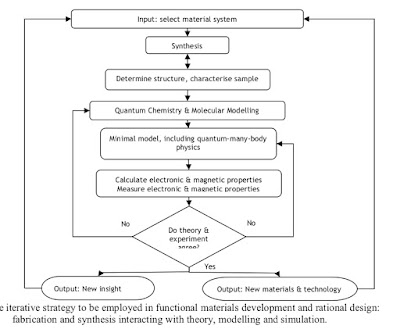




I think a post like this when I was first did research in condensed matter physics would have been very useful to understand some of the bigger picture goals. I remember being introduced to the Hubbard model and seeing its purpose as a simple Hamiltonian that was still hard to solve, so that it was really the 'best' we could do. It took me a while to realise the value of explaining experiments with the fewest degrees of freedom and interactions in order to determine what was actually important for the physics, and why simple models like the Hubbard model was so important for that.
ReplyDeleteQuite well summarized! I surmise I've had at least one B, one C and one D in my life. But I can only say that to some degree of certainty: the further complexity that needs to be mentioned is that A,B,C,D are not mutually "or" options to decide on -- they can all contribute at the same time, which can then lead to multiple, competing theoretical models.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDelete