First-order transitions and critical points in spin-crossover compounds

An interesting feature of spin-crossover compounds is that the transition from low-spin to high-spin with increasing temperature is usually a first-order phase transition. This is associated with hysteresis and the temperature range of the hysteresis varies significantly between compounds.
If there was no interaction between the transition metal ions the transition would be a smooth crossover. This is nicely illustrated in a figure taken from the paper below.

Abrupt versus Gradual Spin-Crossover in FeII(phen)2(NCS)2 and FeIII(dedtc)3 Compared by X-ray Absorption and Emission Spectroscopy and Quantum-Chemical Calculations 
Stefan Mebs, Beatrice Braun, Ramona Kositzki, Christian Limberg, and Michael Haumann

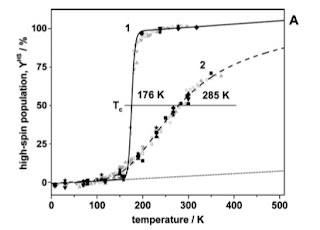
For the first compound, the transition is abrupt [much earlier work found a narrow hysteresis region of about 0.15 K]. For the second compound, the transition is a crossover.

The authors fit their data to an empirical equation that has a parameter n, describing the "interactions". You have to read the Supplementary Material to find the details. This equation cannot describe hysteresis.

 However, there is an elegant analytical theory going back to a paper by Wajnflasz and Pick from 1971. This is nicely summarised in the first section of a paper by Kamel Boukheddaden, Isidor Shteto, Benoit Hôo, and François Varret.

The system can be described by the Ising model

where the Ising spin denotes the high- and low-spin states. Delta is the energy difference between them and ln g the entropy difference.
The mean-field Hamiltonian for q nearest neighbours is

There are two independent dimensionless variables, d and r. Solving for the fraction of high-spin states (HS) versus temperature gives the graphs below for different values of d.

The vertical arrows show the hysteresis region for a specific value of d=2. 

As d increases the hysteresis region gets smaller. Above the critical value of d=r/2, the crossover temperature T0=Delta/ln g is larger than the mean-field critical temperature Tc= qJ, and the transition is no longer first-order but a crossover.

Using DFT-based quantum chemistry the authors calculate the change in vibrational frequencies and the associated entropy change for the SCO transition in a single molecule. The values for compound 1 and 2 are 0.68  and 0.21 meV/K respectively. The spin entropy changes are 0.21and 0.22 meV/K respectively. The total entropy changes are thus 0.89 and 0.43 meV/K respectively. The values of Delta are 175 and 125 meV, respectively. The corresponding crossover temperatures are 210 and 360 K, compared to the experimental values of 176 and 285 K.

If we assume that J is roughly the same for both compounds then the fact that the entropy change is half as big for compound 2, means r is twice as big. This naturally explains why the second compound has a smooth crossover, compared to the first, which is very close to the critical point.