Coupling of the lattice to spin-crossover transitions

There is a very nice paper
Complete Set of Elastic Moduli of a Spin-Crossover Solid: Spin-State Dependence and Mechanical Actuation 
Mirko Mikolasek, Maria D. Manrique-Juarez, Helena J. Shepherd, Karl Ridier, Sylvain Rat, Victoria Shalabaeva, Alin-Ciprian Bas, Ines E. Collings, Fabrice Mathieu, Jean Cacheux, Thierry Leichle, Liviu Nicu, William Nicolazzi, Lionel Salmon, Gábor Molnár, and Azzedine Bousseksou

It investigates the spin-crossover in a specific compound with a suite of techniques, including x-ray diffraction, inelastic neutron scattering, and micro-electromechanical systems (MEMS).

The nice results reflect significant advances over the past few decades in neutron scattering and microfabrication.

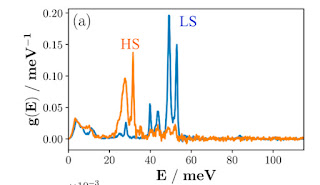
The graph below shows the vibrational density of states of the Fe nuclei and the low-spin (LS) and high-spin (HS) states. Note how the LS modes around 50 meV (400 cm-1) soften significantly in the HS state. These modes are the Fe-N stretches in the octahedron. This softening is associated with a significant increase in entropy which helps drive the spin-crossover transition.
Note that there is a small parabolic part at low energies of a few meV.


The figure below is a "blow up" of the low energy data. 
The energy resolution is amazing! 
The graph shows the density of states divided by E^2. 
Why?
In an isotropic solid (or a powder such as used here) in the Debye model for phonons, the density of states is proportional to E^2 and the proportionality is determined by the speed of sound, v_D.



One clearly sees several things.
1. For E less than about 3 meV, the DOS is quadratic in E, as predicted by Debye.
2. The lattice softens with the spin-crossover.
3. The deviation from quadratic occurs at a smaller E for HS than LS.

The values of the speed of sound can be combined with the lattice constant to estimate the Debye frequency, which is roughly where the deviation from quadratic dependence should occur.
I have done this (since the authors don't appear to have) and one gets values of the order of a few meV, consistent with experiment.

From the speed of sound, one can also determine the Young's modulus. This can then be compared to the bulk modulus, which can be determined from MEMS. The values obtained by these different methods are consistent with one another.
Overall, the values of the bulk modulus for different spin-crossover complexes, of order 5-10 GPa, are comparable to those for organic molecular crystals.

Comments

Post a Comment

Popular posts from this blog

What is Herzberg-Teller coupling?

Image
Is it something to do with breakdown of the Born-Oppenheimer approximation? In molecular spectroscopy you occasionally hear this term thrown around. Google scholar yields more than 3000 hits. But I have found its precise meaning and the relevant physics hard to pin down. Quantum mechanics in chemistry by Schatz and Ratner is an excellent book , but the discussion on page 204 did not help me. "Herzberg-Teller" never appears in Atkins' Molecular quantum mechanics. So here is my limited understanding. Herzberg and Teller wanted to understand why one observed certain vibronic (combined electronic and vibrational) transitions that were not expected, particularly some that were expected to be forbidden on symmetry grounds. " Intensity borrowing " occurred. Herzberg and Teller pointed out that his could be understood if the dipole transition moment for the electronic transition depended on the nuclear co-ordinate associated with the vibration. In the Franck-Condo
Read more

Is it an Unidentified Superconducting Object (USO)?

If you look on the arXiv and in Nature journals there is a continuing stream of people claiming to observe superconductivity in some new material. There is a long history of this and it is worth considering the wise observations of Robert Cava , back in 1997, contained in a tutorial lecture. It would have been useful indeed in the early days of the field [cuprate superconductors] to have set up a "commission" to set some minimum standard of data quality and reproducibility for reporting new superconductors. An almost countless number of "false alarms" have been reported in the past decade, some truly spectacular. Koichi Kitazawa from the University of Tokyo coined these reports "USOs", for Unidentified Superconducting Objects , in a clever cross-cultural double entendre likening them to UFOs (Unidentified Flying Objects, which certainly are their equivalent in many ways) and to "lies" in the Japanese translation of USO.   These have caused g
Read more

What should be the order of authors on a conference poster or talk?

I welcome discussion on this point. I don't think it is as sensitive or as important a topic as the author order on papers. With regard to paper authorship my general rule is that the person who does the bulk of the work, including actually writing the paper should be the first author. Doug Natelson has a good post on co-authorship , that I largely agree with. My only difference is that I am not really convinced that good practice prevails in the majority of circumstances. I fear there are increasing numbers of co-authors, particularly senior ones, with marginal contributions. But, what about conference talks and posters? Many of these are based on work that is already or about to be published. Should the author order be identical as the associated papers? I am not sure it should necessarily be. My tentative view is that the person who writes and submits the abstract and actually prepares and presents the post/talk should be the first author. Perhaps they should also highlig
Read more