Over the years I have moved into new established research areas with mixed success.
Sometimes this has been a move from one sub-field of condensed matter theory to another. Other times it has been to try and cross disciplines, e.g. into theoretical chemistry.
I have also watched with interest as others have tried to break into communities I have been a part of.
Here is my list of suggestions as to things that may increase your chances of success.
1. Listen.
What do the well established experts in the field say? What are they working on? What do they think are the important questions? What are the key concepts and landmarks in the field?
Bear in mind the values and culture may be quite different from your own field.
Note: this is the economist Paul Krugman's first research tip.
2. Be humble.
Most fields have a long history and have been pioneered by some very smart and hard working people. That doesn't mean that the field isn't populated by some mediocre people or bad ideas or bad results or that you have nothing to contribute. But, don't presume that you actually understand the field or that your new "idea" or "contribution" is going to be well received. Treating people in the field with disdain and/or making bold unsubstantiated claims will increase resistance to your ideas. Don't be the scientist who cried "Breakthrough!"
3. Be patient.
Don't expect people to instantly understand what you are on about or how important your contribution is. It may take years or decades to be accepted.
4. Make personal connections.
Go to conferences. Talk to people. Slowly and carefully explain what you are doing. Learn from them.
Who is your real audience?
Are you just trying to impress your department chair, a funding agency, or your home discipline, by claiming that what you are doing is relevant to other research areas? Or are you actually trying to make a real contribution to a different community?
If you want to see a case of physicists not being well received in biology read Aaaargh! Physicists! Again! by PZ Myers about a new theory of cancer proposed by Paul Davies and Charles Lineweaver.
An article by Davies about his theory is the cover story of the latest issue of Physics World.
I welcome suggestions and anecdotes.
Wednesday, July 31, 2013
Tuesday, July 30, 2013
Imaging proton probability distributions in hydrogen bonding
As the strength of hydrogen bonds varies there are significant qualitative changes in the effective Born-Oppenheimer potential that the proton moves in [double well, low barrier double well, single well]. These changes will lead to qualitative differences in the ground state probability distribution for the proton. How does one measure this probability distribution?
Over the past decade this has become possible with deep inelastic neutron scattering.
Calculation of the probability distribution functions using path integral techniques with potentials from Density Functional Theory (DFT) is considered in
Tunneling and delocalization effects in hydrogen bonded systems: A study in position and momentum space
by Joseph Morrone, Lin Lin, and Roberto Car
They consider three different situations, O-H...O, shown below, and corresponding to average proton donor-acceptor (oxygen-oxygen) distances of 2.53, 2.45, and 2.31 Angstroms respectively (top to bottom). They also correspond to three different phases of ice. I discussed Ice X earlier.
This is what one actually measures in the experiment.
Hence, one may worry whether one can really discern qualitative differences by finding small quantitative differences.
But the experimentalists claim they can.
Below are the results from a PRL
Anomalous Behavior of Proton Zero Point Motion in Water Confined in Carbon Nanotubes
Over the past decade this has become possible with deep inelastic neutron scattering.
Calculation of the probability distribution functions using path integral techniques with potentials from Density Functional Theory (DFT) is considered in
Tunneling and delocalization effects in hydrogen bonded systems: A study in position and momentum space
by Joseph Morrone, Lin Lin, and Roberto Car
They consider three different situations, O-H...O, shown below, and corresponding to average proton donor-acceptor (oxygen-oxygen) distances of 2.53, 2.45, and 2.31 Angstroms respectively (top to bottom). They also correspond to three different phases of ice. I discussed Ice X earlier.
The three corresponding probability distributions for the proton along the oxygen-oxygen distance are shown below. System 1, 2, and 3 correspond to Ice X, VII, and VIII, respectively.
Notice the clear qualitative differences between the distributions in real space.
Now here is the surprising (and disappointing) thing.
The momentum space probability distributions are not that different, as seen below.
[I wish they had plotted system 1 as well].
Hence, one may worry whether one can really discern qualitative differences by finding small quantitative differences.
But the experimentalists claim they can.
Below are the results from a PRL
Anomalous Behavior of Proton Zero Point Motion in Water Confined in Carbon Nanotubes
n.b. they seem to be claiming that the oxygen-oxygen distance is only 2.1 A for the water inside the nanotube, considerably less than in bulk water or even ice X. Is this realistic or understandable?
When the potential has a barrier [but not necessarily tunneling] the momentum distribution has a node at high momentum. Morrone, Lin, and Car reproduce this is a simple model calculation but find that their path integral simulations cannot resolve it.
Monday, July 29, 2013
Improving Wikipedia on condensed matter
For a long time I have been meaning to write this post. It was finally stimulated by seeing that the Electronic Structure Theory community has started an initiative to improve the Wikipedia articles relevant to their community.
I think most of the articles relevant to theoretical condensed matter physics and chemistry are quite poor or non-existent. We need to take responsibility for that.
I think the simplest way forward may be for us to encourage our graduate students to write and update articles for Wikipedia. Many draft literature reviews for undergrad, Masters, and Ph.D theses could be used as starting points. For that matter some of my blog posts, could be too. It could be quite educational for students to post material and hopefully see it revised.
I think most of the articles relevant to theoretical condensed matter physics and chemistry are quite poor or non-existent. We need to take responsibility for that.
I think the simplest way forward may be for us to encourage our graduate students to write and update articles for Wikipedia. Many draft literature reviews for undergrad, Masters, and Ph.D theses could be used as starting points. For that matter some of my blog posts, could be too. It could be quite educational for students to post material and hopefully see it revised.
Friday, July 26, 2013
Dispersion kinks and spin fluctuations
A recent post considered the problem of deconstructing the kinks that occur in energy versus wavevector dispersion relations in some strongly correlated electron systems.
I have now read two of the related references to the recent PRL I discussed. A nice earlier PRL discusses how kinks occur in the temperature dependence of the specific heat. Furthermore, the authors use an obscure formula from the classic AGD to show that these kinks are related to the kinks in the self energy.
Emergent Collective Modes and Kinks in Electronic Dispersions
Carsten Raas, Patrick Grete, and Götz S Uhrig
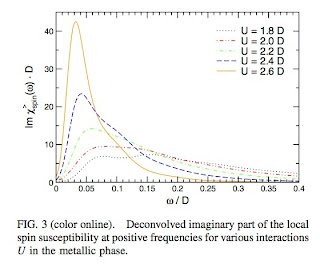
They calculate the self energy and the frequency dependent local spin susceptibility for the Hubbard model at half filling using Dynamical Mean-Field Theory (DMFT). The latter quantity is shown below. As the Mott insulator is approached a low-energy peak develops in the spin susceptibility. This reflects the large spin fluctuations in the metallic phase as the electrons become more localised.
From the correlation shown above the authors "deduce" that the spin fluctuations "cause" the kink. I suspect this has to be true but the logic does not appear completely water tight to me.
Nevertheless, it is a beautiful result.
All this is at zero temperature. I would be very interested to see how the spin susceptibility evolves with increasing temperature, particularly as one goes into the bad metal region.
It would also be interesting to see how this physics persists beyond DMFT.
I have now read two of the related references to the recent PRL I discussed. A nice earlier PRL discusses how kinks occur in the temperature dependence of the specific heat. Furthermore, the authors use an obscure formula from the classic AGD to show that these kinks are related to the kinks in the self energy.
Emergent Collective Modes and Kinks in Electronic Dispersions
Carsten Raas, Patrick Grete, and Götz S Uhrig
They calculate the self energy and the frequency dependent local spin susceptibility for the Hubbard model at half filling using Dynamical Mean-Field Theory (DMFT). The latter quantity is shown below. As the Mott insulator is approached a low-energy peak develops in the spin susceptibility. This reflects the large spin fluctuations in the metallic phase as the electrons become more localised.
Aside: the slope of this curve at zero frequency is proportional to the NMR relaxation rate 1/T_1.
The frequency/energy of the peak is the same as the frequency of the kink in the self energy and the local Greens function, as shown below.
Note how there is an emergent low-energy scale much less than the energy scales in the Hamiltonian; a profound characteristic feature of strongly correlated systems.From the correlation shown above the authors "deduce" that the spin fluctuations "cause" the kink. I suspect this has to be true but the logic does not appear completely water tight to me.
Nevertheless, it is a beautiful result.
All this is at zero temperature. I would be very interested to see how the spin susceptibility evolves with increasing temperature, particularly as one goes into the bad metal region.
It would also be interesting to see how this physics persists beyond DMFT.
Thursday, July 25, 2013
The formidable challenge of science in the majority world
I am very proud to have my first paper published in the Journal of Chemical Education!
Moreover, I believe it concerns a very important topic
Connecting Resources for Tertiary Chemical Education with Scientists and Students in Developing Countries
The paper was written with Ross Jansen-van Vuuren (UQ) and Malcolm Buchanan (St. John's University, Tanzania)
The abstract is
Moreover, I believe it concerns a very important topic
Connecting Resources for Tertiary Chemical Education with Scientists and Students in Developing Countries
The paper was written with Ross Jansen-van Vuuren (UQ) and Malcolm Buchanan (St. John's University, Tanzania)
The abstract is
The ability of developing countries to provide a sound tertiary chemical education is a key ingredient to the improvement of living standards and economic development within these countries. However, teaching undergraduate experimental chemistry and building research capacity in institutions based within these countries involves formidable challenges. These are not just a lack of funding and skilled teachers and technicians, but also take the form of cultural and language barriers. In the past three decades a diverse range of initiatives have aimed to address the situation. This article provides a summary of these while conveying realistic and concrete suggestions for how scientists based in industrialized nations can get involved, based on low-cost solutions with existing resources. The first step is being well informed about what has already been tried and what currently works.Many of the same issues apply in physics. But, since my co-authors were chemists with relevant experience we focused on chemistry. In preparing the article I was struck by just how much is being done, how great the challenges are, and how people sometimes dive into this challenging enterprise without considering what else is going on and what has been tried before. This is why we wrote the review. Hopefully, it will stimulate more efforts.
Wednesday, July 24, 2013
Vignettes of bad metal conference
Here is a random collection of a few of the things I learnt last week in Korea.
Yuji Matsuda described experimental work on the iron pnictides which shows evidence [via a diverging effective mass] for a Quantum critical point hidden beneath the superconducting dome.
Jan Zaanen gave an interesting talk about AdS/CFT correspondence techniques from string theory.
I am slowly becoming less skeptical about this surreal enterprise. Some concrete results that could conceivably relevant to experiment are being produced. Zaanen mentioned work by Gary Horowitz and Jorge Santos that produces a frequency-dependent conductivity that has some similarities to what is observed in the cuprates. [But, one needs to consider the alternative explanation]. I was disappointed that Zaanen ignored the work described in this post, claiming that interlayer "incoherence" in the cuprates is a mystery.
Henri Alloul recently posted on the arXiv What is the simplest model which captures the basic experimental facts of the physics of underdoped curates?
He is an experimentalist who has worked on the cuprates since the beginning. His answer is the one-band Hubbard model and Cellular Dynamical Mean-Field Theory captures the essential details.
I agree.
Alloul's text Introduction to the Physics of Electrons in Solids has been translated into English. It has a particularly nice set of problems in it.
Aharon Kapitulnik gave a talk about Polar Kerr effect as probe for time-reversal symmetry breaking (TRSB) in unconventional superconductor. He has an instrument that can measure the magneto-optic Faraday or Kerr effects with a sensitivity of 10 nano radians! They have observed TRSB in Sr2RuO4 and the "hidden order" and superconducting states of the heavy fermion compound URu2Si2.
Non-zero Kerr effects are also seen in the pseudogap state. They can be interpreted in terms of TRSB or "gyrotopic"/chiral order associated with stripe order. [It seems the Berry phase may play a role there].
Isao Inoue, Marcelo Rozenberg and Hyuntak Kim gave talks about the emerging field of Mottronics: building transistors based on the Mott metal-insulator transition. A recent review of the field is here.
There was more, but that is enough for now...
Yuji Matsuda described experimental work on the iron pnictides which shows evidence [via a diverging effective mass] for a Quantum critical point hidden beneath the superconducting dome.
Jan Zaanen gave an interesting talk about AdS/CFT correspondence techniques from string theory.
I am slowly becoming less skeptical about this surreal enterprise. Some concrete results that could conceivably relevant to experiment are being produced. Zaanen mentioned work by Gary Horowitz and Jorge Santos that produces a frequency-dependent conductivity that has some similarities to what is observed in the cuprates. [But, one needs to consider the alternative explanation]. I was disappointed that Zaanen ignored the work described in this post, claiming that interlayer "incoherence" in the cuprates is a mystery.
Henri Alloul recently posted on the arXiv What is the simplest model which captures the basic experimental facts of the physics of underdoped curates?
He is an experimentalist who has worked on the cuprates since the beginning. His answer is the one-band Hubbard model and Cellular Dynamical Mean-Field Theory captures the essential details.
I agree.
Alloul's text Introduction to the Physics of Electrons in Solids has been translated into English. It has a particularly nice set of problems in it.
Aharon Kapitulnik gave a talk about Polar Kerr effect as probe for time-reversal symmetry breaking (TRSB) in unconventional superconductor. He has an instrument that can measure the magneto-optic Faraday or Kerr effects with a sensitivity of 10 nano radians! They have observed TRSB in Sr2RuO4 and the "hidden order" and superconducting states of the heavy fermion compound URu2Si2.
Non-zero Kerr effects are also seen in the pseudogap state. They can be interpreted in terms of TRSB or "gyrotopic"/chiral order associated with stripe order. [It seems the Berry phase may play a role there].
Isao Inoue, Marcelo Rozenberg and Hyuntak Kim gave talks about the emerging field of Mottronics: building transistors based on the Mott metal-insulator transition. A recent review of the field is here.
There was more, but that is enough for now...
Tuesday, July 23, 2013
Are physical chemists Bohmians?
I doubt it. They are just pragmatists.
Today we had an interesting Quantum Science Seminar by Peter Riggs, author of Quantum Causality: Conceptual Issues in the Causal Theory of Quantum Mechanics.
Other names for the causal theory are Bohmian mechanics, De Broglie's pilot-wave theory, ontological quantum theory...
The talk provided a nice overview of the theory and different objections to it. Riggs is an advocate of the theory, claiming it "solves" the measurement problem.
He does not seem concerned that relativistic and spin versions of the theory seem a rare species or intractable.
I was intrigued that Riggs invoked physical chemists, such as Robert E. Wyatt, in a manner that suggested that they were advocates of the theory. Wyatt has had considerable success in applying the mathematics of Bohmian mechanics to solve quantum dynamics problems in chemistry. He is the author of Quantum dynamics with trajectories. However, my impression is that Wyatt and his collaborators are purely motivated by the fact that the Bohmian equations [without any philosophy attached] allow considerable computational savings. They are just a different way of encoding the standard quantum physics.
In fact, in a comment on a Science paper "Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer"[which incidentally contained lots of technical errors...] Wyatt concludes
Today we had an interesting Quantum Science Seminar by Peter Riggs, author of Quantum Causality: Conceptual Issues in the Causal Theory of Quantum Mechanics.
Other names for the causal theory are Bohmian mechanics, De Broglie's pilot-wave theory, ontological quantum theory...
The talk provided a nice overview of the theory and different objections to it. Riggs is an advocate of the theory, claiming it "solves" the measurement problem.
He does not seem concerned that relativistic and spin versions of the theory seem a rare species or intractable.
I was intrigued that Riggs invoked physical chemists, such as Robert E. Wyatt, in a manner that suggested that they were advocates of the theory. Wyatt has had considerable success in applying the mathematics of Bohmian mechanics to solve quantum dynamics problems in chemistry. He is the author of Quantum dynamics with trajectories. However, my impression is that Wyatt and his collaborators are purely motivated by the fact that the Bohmian equations [without any philosophy attached] allow considerable computational savings. They are just a different way of encoding the standard quantum physics.
In fact, in a comment on a Science paper "Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer"[which incidentally contained lots of technical errors...] Wyatt concludes
Many adherents to Bohm’s version of quantum mechanics assert that the trajectories are what particles actually do in nature. From the experimental results above no one would claim that photons actually traversed these trajectories, since the momentum was only measured on average and the pixel size of the CCD is still quite large. Other views of Bohm’s trajectories do not go as far as to claim that they are what particles actually do in nature. But instead, the Bohm trajectories can be viewed simply as hydrodynamical trajectories [5, 7] that have equations of motion with an internal force that appears when one changes from a phase space to a position space discription. Recently, it has also been shown that the Bohm trajectories can in fact be generated without any equations of motion ...., one concludes again that they Bohm trajectories are simply hydrodynamical and kinematically portraying the evolution of the probability density. The average photon trajectories can be viewed likewise.So, Eric Bittner, are you a Bohmian? or just a pragmatic quantum guy?
Monday, July 22, 2013
Science is all about comparisons
It amazes and frustrates me that this basic point is so often neglected.
Comparisons are central to science in two respects.
Control variables.
As you vary just ONE parameter [pressure, electron-phonon coupling, temperature, isotope, Planck's constant] how do the results of the experiment or calculation vary.
People seem to often vary more than one parameter.
Or, they don't vary any. For example, they do some complicated calculation and get "an answer", i.e. a number, but don't investigate or report how that answer depends on the parameters or approximations in their calculation.
Comparison with earlier work.
Many people don't seem to feel a need or obligation to report how their results compare to those of others who did related experiments or simulations.
Earlier I made the case for why Tables are wonderful in papers for these reasons.
I also considered the astonishing case of a widely downloaded paper about the theory of hydrogen bonding that tried to make a case that there was no reason to compare the calculations to experiment.
It is interesting to me how often people neglect to make such comparisons. Yet after they give a talk these are often the first questions that are asked.
Do you agree this is a problem?
If so, why are people so reluctant to make comparisons?
Are they just lazy? Or scared?
Comparisons are central to science in two respects.
Control variables.
As you vary just ONE parameter [pressure, electron-phonon coupling, temperature, isotope, Planck's constant] how do the results of the experiment or calculation vary.
People seem to often vary more than one parameter.
Or, they don't vary any. For example, they do some complicated calculation and get "an answer", i.e. a number, but don't investigate or report how that answer depends on the parameters or approximations in their calculation.
Comparison with earlier work.
Many people don't seem to feel a need or obligation to report how their results compare to those of others who did related experiments or simulations.
Earlier I made the case for why Tables are wonderful in papers for these reasons.
I also considered the astonishing case of a widely downloaded paper about the theory of hydrogen bonding that tried to make a case that there was no reason to compare the calculations to experiment.
It is interesting to me how often people neglect to make such comparisons. Yet after they give a talk these are often the first questions that are asked.
Do you agree this is a problem?
If so, why are people so reluctant to make comparisons?
Are they just lazy? Or scared?
Saturday, July 20, 2013
Are large atomistic quantum dynamical simulations falsifiable?
There are a whole range of dynamical processes found in biomolecular systems that one would like to simulate and understand. Examples include:
However, it is important to bear in mind the many ingredients and many approximations employed, at each level of the simulation. These can include
If there are 10 approximations involving errors of 20 per cent each, what is the likely error in the whole simulation? Obviously, it is actually much more complicated than this. Will the errors be additive or independent of one another? Or is one hoping for some sort of cancellation of errors?
What is one really hoping to achieve with these simulations?
In what sense are they falsifiable?
When they disagree with experiment what does one conclude?
An earlier post highlighted the critical assessment of one expert, Daan Frenkel of the role of classical simulations. I hope we will see a similar assessment of quantum simulations in molecular biophysics.
- charge separation at the photosynthetic reaction centre
- proton transfer in an enzyme
- photo-isomerisation of a fluorescent protein
- exciton migration in photosynthetic systems.
These are particularly interesting and challenging because they lie at the quantum-classical boundary. There is a subtle interaction between a quantum subsystem [e.g. the ground and excited electronic states of a chromophore] and the environment [the surrounding protein and water] whose dynamics are largely classical.
[image from here]
Due to recent advances in computational power and new algorithms [some based on conceptual advances] it is now possible to perform simulations with considerable atomistic detail. This is an example of "multi-scale" modeling.
Due to recent advances in computational power and new algorithms [some based on conceptual advances] it is now possible to perform simulations with considerable atomistic detail. This is an example of "multi-scale" modeling.
However, it is important to bear in mind the many ingredients and many approximations employed, at each level of the simulation. These can include
- uncertainty in the actual protein structure
- the force fields used for the classical dynamics of the surrounding water
- the atomic basis sets used in "on the fly" quantum chemistry calculations
- density functionals used [if DFT is a component]
- surface hopping for non-adiabatic dynamics [e.g. non-radiative decay of an excited state].
These approximations can be quite severe. For example, a widely used water force field used in biomolecular simulations, TIP3P, predicts that water freezes as -130 degrees Centigrade!
Then there is the whole question of how one decides on how to divide the quantum and classical parts of the simulation.
If there are 10 approximations involving errors of 20 per cent each, what is the likely error in the whole simulation? Obviously, it is actually much more complicated than this. Will the errors be additive or independent of one another? Or is one hoping for some sort of cancellation of errors?
What is one really hoping to achieve with these simulations?
In what sense are they falsifiable?
When they disagree with experiment what does one conclude?
An earlier post highlighted the critical assessment of one expert, Daan Frenkel of the role of classical simulations. I hope we will see a similar assessment of quantum simulations in molecular biophysics.
Friday, July 19, 2013
Unified phase diagram for iron and cuprate superconductors
At the workshop this week Luca de' Medici gave a nice talk, based on work described in a preprint Selective Mottness as a key to iron superconductors with Gianluca Giovannetti, Massimo Capone
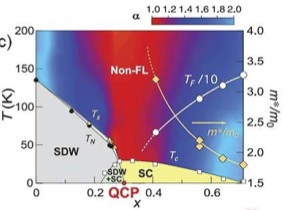
They argue that the best way to understand the iron superconductors is in terms of Hund's rule coupling and the total orbital filling. Thus the "parent compounds" which are antiferromagnetic should be viewed as being at 0.2 doping because they have 5 electrons in 3 degenerate iron orbitals. If one airbrushes out the antiferromagnetic phase one is left with the phase diagram below.
This has a rather striking resemblance to the cuprate phase diagram (!), particularly when the pseudogap phase can be viewed as a "momentum selective" Mott insulator.
They argue that the best way to understand the iron superconductors is in terms of Hund's rule coupling and the total orbital filling. Thus the "parent compounds" which are antiferromagnetic should be viewed as being at 0.2 doping because they have 5 electrons in 3 degenerate iron orbitals. If one airbrushes out the antiferromagnetic phase one is left with the phase diagram below.
This has a rather striking resemblance to the cuprate phase diagram (!), particularly when the pseudogap phase can be viewed as a "momentum selective" Mott insulator.
Thursday, July 18, 2013
The tide is turning against impact factors
Bruce Alberts, Editor in Chief of Science, has a powerful editorial Impact Factor Distortions. Here is the beginning and the end.
This Editorial coincides with the release of the San Francisco declaration on research Assessment (DORA), the outcome of a gathering of concerned scientists at the December 2012 meeting of the American Society for Cell Biology. To correct distortions in the evaluation of scientific research, DORA aims to stop the use of the "journal impact factor" in judging an individual scientist's work. The Declaration states that the impact factor must not be used as "a surrogate measure of the quality of individual research articles, to assess an individual scientist's contributions, or in hiring, promotion, or funding decisions." DORA also provides a list of specific actions, targeted at improving the way scientific publications are assessed, to be taken by funding agencies, institutions, publishers, researchers, and the organizations that supply metrics. These recommendations have thus far been endorsed by more than 150 leading scientists and 75 scientific organizations, including the American Association for the Advancement of Science (the publisher ofScience).....
As a bottom line, the leaders of the scientific enterprise must accept full responsibility for thoughtfully analyzing the scientific contributions of other researchers. To do so in a meaningful way requires the actual reading of a small selected set of each researcher's publications, a task that must not be passed by default to journal editors.
Wednesday, July 17, 2013
Is hydrodynamics ever relevant in metals?
This is a very subtle question. I learnt a lot from a nice talk that Steve Kivelson gave on the subject.
In a single component fluid [e.g. water or a gas] a hydrodynamic approach works because one has local conversation of energy and momentum. Then ALL transport properties are determined by just three quantities: the shear viscosity (eta), the second viscosity (zeta), and the thermal conductivity (kappa).
However, the electron fluid in a solid can exchange energy and momentum with the lattice and impurities. Hence, hydrodynamics is not relevant.
What about temperature ranges where electron-electron scattering dominates? Well then one has resistivity as a result of Umklapp scattering, which means that there is momentum exchange with the lattice. [I never understand all the subtle details of that]. Hence, one still does not have conditions under which hydrodynamics may apply.
So when might hydrodynamics apply? Kivelson suggests it may be relevant in 2DEGS [2-Dimensional Electron Gases] in semiconductor heterostructures close to the metal-insulator transition. Then the lattice is irrelevant and the electron-electron scattering is dominant. What causes resistivity? It can be collision of the fluid with "large" objects such as some slowly varying background impurity potential. Andreev, Kivelson, and Spivak calculated the two-dimensional resistivity as
where the averaging is over space and n0 and s0 denote the equilibrium density and entropy. An important point is that the resistivity is proportional to the viscosity. In simple kinetic theory this is proportional to the scattering time. In a Fermi liquid this will increase with decreasing temperature. Thus the resistivity will have the opposite temperature dependence to a conventional metal!
Hydrodynamics in metals opens the possibility of turbulence. Signatures of this will be nonlinear I-V characteristics, dependence on geometry, and noise.
Kivelson also highlighted relevant recent work by his string theory colleagues on breakdown of the Wiedemann-Franz law in non-Fermi liquids.
A previous post considered the problem of the viscosity of bad metals.
In a single component fluid [e.g. water or a gas] a hydrodynamic approach works because one has local conversation of energy and momentum. Then ALL transport properties are determined by just three quantities: the shear viscosity (eta), the second viscosity (zeta), and the thermal conductivity (kappa).
However, the electron fluid in a solid can exchange energy and momentum with the lattice and impurities. Hence, hydrodynamics is not relevant.
What about temperature ranges where electron-electron scattering dominates? Well then one has resistivity as a result of Umklapp scattering, which means that there is momentum exchange with the lattice. [I never understand all the subtle details of that]. Hence, one still does not have conditions under which hydrodynamics may apply.
So when might hydrodynamics apply? Kivelson suggests it may be relevant in 2DEGS [2-Dimensional Electron Gases] in semiconductor heterostructures close to the metal-insulator transition. Then the lattice is irrelevant and the electron-electron scattering is dominant. What causes resistivity? It can be collision of the fluid with "large" objects such as some slowly varying background impurity potential. Andreev, Kivelson, and Spivak calculated the two-dimensional resistivity as
where the averaging is over space and n0 and s0 denote the equilibrium density and entropy. An important point is that the resistivity is proportional to the viscosity. In simple kinetic theory this is proportional to the scattering time. In a Fermi liquid this will increase with decreasing temperature. Thus the resistivity will have the opposite temperature dependence to a conventional metal!
Hydrodynamics in metals opens the possibility of turbulence. Signatures of this will be nonlinear I-V characteristics, dependence on geometry, and noise.
Kivelson also highlighted relevant recent work by his string theory colleagues on breakdown of the Wiedemann-Franz law in non-Fermi liquids.
A previous post considered the problem of the viscosity of bad metals.
Clarifying the "Rashba" effect
At the conference today Changyoung Kim gave a nice talk about how the "Rashba effect" [coupling of momentum and spin] on the surface of a semiconductor has a different physical origin to what is usually claimed. In particular, the energy scale for the relativistic Zeeman splitting proposed by Rashba gives a band splitting that is six orders of magnitude smaller than what is actually observed!
Here is the abstract of the associated PRL:
Here is the abstract of the associated PRL:
We propose that the existence of local orbital angular momentum (OAM) on the surfaces of high-Z materials plays a crucial role in the formation of Rashba-type surface band splitting. Local OAM state in a Bloch wave function produces an asymmetric charge distribution (electric dipole). The surface-normal electric field then aligns the electric dipole and results in chiral OAM states and the relevant Rashba-type splitting. Therefore, the band splitting originates from electric dipole interaction, not from the relativistic Zeeman splitting as proposed in the original Rashba picture. The characteristic spin chiral structure of Rashba states is formed through the spin-orbit coupling and thus is a secondary effect to the chiral OAM.
Monday, July 15, 2013
Hund's rule coupling promotes bad metals
There is a nice review Strong correlations from Hund's coupling by
Antoine Georges, Luca de' Medici, and Jernej Mravlje.
Section 6 describes
A previous post describing some of this work includes Hund's rule coupling in multi-band metals.
Antoine Georges, Luca de' Medici, and Jernej Mravlje.
Section 6 describes
the main physical point of this review: Generally, the Hund’s rule coupling has a conflicting effect on the physics of the solid-state. On the one hand, it increases the critical U above which a Mott insulator is formed (Section 3); on the other hand, it reduces the temperature and the energy scale below which a Fermi liquid is formed, leading to a (bad) metallic regime in which quasiparticle coherence is suppressed (Section 4).In particular, this means a new organising principle for strong correlated electron systems: one can have a bad metal and be a long way from a Mott insulator. "Mottness" is not the only ingredient for strong correlations.
A previous post describing some of this work includes Hund's rule coupling in multi-band metals.
Talk on bad metals in Korea
This week I am at a meeting Bad metal behavior and Mott quantum criticality being held at POSTECH in Korea. Here is the current version of the slides for my talk, "Organic charge transfer salts: model bad metals near a Mott transition." The main results in the talk are in a recent PRL, written with Jure Kokalj.
Aside: Unfortunately, I am missing the beginning of the meeting. I got stuck in Tokyo because of a delayed flight from Denver. On this leg of my trip it seems flying in and out of Denver has been a comedy of errors and delays.
Aside: Unfortunately, I am missing the beginning of the meeting. I got stuck in Tokyo because of a delayed flight from Denver. On this leg of my trip it seems flying in and out of Denver has been a comedy of errors and delays.
Sunday, July 14, 2013
Kinky many-body physics
A key and profound property of quantum-many body systems is the emergence of new low energy scales that are much less than the underlying bare interactions. Classic cases are the Kondo temperature and the superconducting transition temperature in BCS theory. How the relevant low energy scales emerge in strongly correlated electron systems is an outstanding problem.
There is a very nice PRL
Poor Man’s Understanding of Kinks Originating from Strong Electronic Correlations
K. Held, R. Peters, and A. Toschi
A decade ago there was a Nature paper [where else?!] that made a big deal about the fact that they saw a kink in the quasi-particle dispersion [energy versus momentum] of a cuprate material measured by ARPES and claimed this was due to electron-phonon coupling. Hence, (!) electron-phonon coupling must be important in the cuprates. I found this claim troubling because it seemed to be based on the classic fallacy of not distinguishing sufficient and necessary conditions. Just because electron-phonon coupling can produce a kink does not mean that this is the case here. What about alternative explanations? Subsequent theoretical work, showed that electronic correlations [as captured by Dynamical Mean Field Theory (DMFT)] could also produce a kink too. This was hardly surprising to me.
The really interesting and important question is how the low energy scale [~50 meV for the cuprates] associated with the kink emerges. The authors of this PRL show that this energy scale is associated with the crossover to the strong coupling fixed point of the Kondo problem associated with the DMFT treatment of the Hubbard model.
They "emphasize that this is a radically new insight."
I agree.
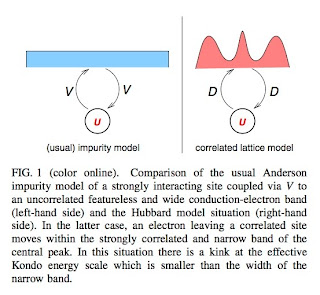
The figure below highlights the difference between the usual Anderson impurity model and the self-consistent Anderson impurity problem associated with DMFT. In the former one has the hybridisation V much less than the conduction band width W which is much less than U. In contrast for the Hubbard DMFT case the hybridisation is replaced by the bare bandwidth D [or the hopping t] which is actually larger than the (renormalised) bandwidth Gamma associated with the central peak in the spectral density.
This different hierarchy of energy scales leads to a new energy scale omega* given by
This expression is derived using a "poor man's" scaling analysis.
The figure below shows the frequency dependency of the real part of the self energy.
At low frequencies it is linear for omega less than omega*, as expected for a Fermi liquid. The slope gives the quasi-particle renormalisation Z.
For higher frequencies it is also approximately linear for frequencies on the scale of the central peak (CP) defining a higher frequency quasi-particle weight.
A few things I would like to know in the future include how these results connect to other work.
1. The details of how this physics affects the temperature dependence of properties. A few qualitative comments are made about temperature dependence in the conclusion.
2. A recent DMFT paper found robust quasi-particles out to much higher temperatures than expected. Is this the same physics?
3. A phenomenological model self energy for the cuprates [described in a PRB by Jure Kokalj, Nigel Hussey, and I] involves crossovers at some low energy scales whose microscopic origin needs to be elucidated.
Aside: On his blog, Doug Natelson had some negative comments about PRL stimulated by the poor abstract and lack of editing (not science) of this paper.
There is a very nice PRL
Poor Man’s Understanding of Kinks Originating from Strong Electronic Correlations
K. Held, R. Peters, and A. Toschi
A decade ago there was a Nature paper [where else?!] that made a big deal about the fact that they saw a kink in the quasi-particle dispersion [energy versus momentum] of a cuprate material measured by ARPES and claimed this was due to electron-phonon coupling. Hence, (!) electron-phonon coupling must be important in the cuprates. I found this claim troubling because it seemed to be based on the classic fallacy of not distinguishing sufficient and necessary conditions. Just because electron-phonon coupling can produce a kink does not mean that this is the case here. What about alternative explanations? Subsequent theoretical work, showed that electronic correlations [as captured by Dynamical Mean Field Theory (DMFT)] could also produce a kink too. This was hardly surprising to me.
The really interesting and important question is how the low energy scale [~50 meV for the cuprates] associated with the kink emerges. The authors of this PRL show that this energy scale is associated with the crossover to the strong coupling fixed point of the Kondo problem associated with the DMFT treatment of the Hubbard model.
They "emphasize that this is a radically new insight."
I agree.
The figure below highlights the difference between the usual Anderson impurity model and the self-consistent Anderson impurity problem associated with DMFT. In the former one has the hybridisation V much less than the conduction band width W which is much less than U. In contrast for the Hubbard DMFT case the hybridisation is replaced by the bare bandwidth D [or the hopping t] which is actually larger than the (renormalised) bandwidth Gamma associated with the central peak in the spectral density.
This different hierarchy of energy scales leads to a new energy scale omega* given by
This expression is derived using a "poor man's" scaling analysis.
The figure below shows the frequency dependency of the real part of the self energy.
At low frequencies it is linear for omega less than omega*, as expected for a Fermi liquid. The slope gives the quasi-particle renormalisation Z.
For higher frequencies it is also approximately linear for frequencies on the scale of the central peak (CP) defining a higher frequency quasi-particle weight.
A few things I would like to know in the future include how these results connect to other work.
1. The details of how this physics affects the temperature dependence of properties. A few qualitative comments are made about temperature dependence in the conclusion.
2. A recent DMFT paper found robust quasi-particles out to much higher temperatures than expected. Is this the same physics?
3. A phenomenological model self energy for the cuprates [described in a PRB by Jure Kokalj, Nigel Hussey, and I] involves crossovers at some low energy scales whose microscopic origin needs to be elucidated.
Aside: On his blog, Doug Natelson had some negative comments about PRL stimulated by the poor abstract and lack of editing (not science) of this paper.
Saturday, July 13, 2013
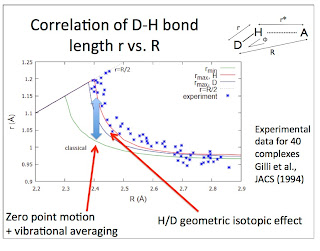
More hydrogen bond correlations
Although hydrogen bonded systems (D-H....A) are chemically diverse and have a wide range of physical properties one observes simple empirical correlations between physical properties and two key variables: the donor-acceptor (D-A) distance R and the difference in proton affinity between the donor and acceptor. That is the main starting point of my paper on the subject.
I am continually learning of more empirical correlations that need to be explained.
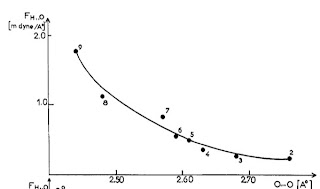
The vibrational frequency for motion of the donor D-H relative to the acceptor A can be measured by infra-red spectroscopy. No particular correlations are observed with R. However, this is because of a diversity of donor and acceptor masses. If instead one uses the frequency and masses to calculate the force constant [the curvature of the hydrogen bond potential] one observes a correlation.
The Figure below is taken from a 1974 review article by Novak.
I believe this correlation is a key ingredient to understanding the secondary geometric isotope effect in hydrogen bonded systems. This is where the donor-acceptor distance changes with deuterium substitution. This is also known as the Ubbelohde effect, after one of the people who discovered it [or at least first highlighted it in 1955]. A portrait of Leo Ubbelohde is shown below. Clearly, he was not very excited about hydrogen bonding!
I thank Angelos Michaelides for bringing the portrait to my attention. When Angelos showed the portrait at the Telluride meeting it caused some amusement.
Correction (15 July, 2014). It turns out this is the wrong Ubbelohde. The correct one is actually Alfred Ubbelohde.
Friday, July 12, 2013
Effect of decoherence on the Berry phase
The Berry (geometric) phase is a significant quantum effect which is associated with conical intersections on excited state potential energy surfaces in molecular photophysics.
An observable consequence is that if a wavepacket is split in two and the two parts traverse opposite sides of the conical intersection (CI) then they will interfere destructively when they meet again on the other side of the CI. [An earlier post considers this effect].
An important question is: what happens to this quantum interference in the presence of decoherence due to the environment?
This question is considered in a nice paper
Quantum-classical description of environmental effects on electronic dynamics at conical intersections
Aaron Kelly and Raymond Kapral
To answer the above question they calculate the probability density on the other side of the CI as a function of the distance from the maximum interference point. This is done for a range of different environment [harmonic oscillator bath] parameters. The key figure is below
In the lower left one sees that there is a dip in the probability at Y=0 due to the quantum interference. The minimum is gradually washed out as the ratio of the bath frequency omega_c to the oscillator frequency omega_x [a measure of the timescale of the semi-classical motion of the wavepackets on the potential energy surface].
I thank Aaron Kelly for helping me understand his work.
An observable consequence is that if a wavepacket is split in two and the two parts traverse opposite sides of the conical intersection (CI) then they will interfere destructively when they meet again on the other side of the CI. [An earlier post considers this effect].
An important question is: what happens to this quantum interference in the presence of decoherence due to the environment?
This question is considered in a nice paper
Quantum-classical description of environmental effects on electronic dynamics at conical intersections
Aaron Kelly and Raymond Kapral
To answer the above question they calculate the probability density on the other side of the CI as a function of the distance from the maximum interference point. This is done for a range of different environment [harmonic oscillator bath] parameters. The key figure is below
In the lower left one sees that there is a dip in the probability at Y=0 due to the quantum interference. The minimum is gradually washed out as the ratio of the bath frequency omega_c to the oscillator frequency omega_x [a measure of the timescale of the semi-classical motion of the wavepackets on the potential energy surface].
I thank Aaron Kelly for helping me understand his work.
Thursday, July 11, 2013
The importance of "down time"
I am not sure that Sheldon Cooper should be considered as a useful source of advice, either personal or scientific [he is a string theorist!]. Nevertheless, the clip below shows he does understand the importance of "down time", particularly for introverts.
This is something that it took me too many years to learn.
I think the need for this quiet time is particularly true at busy meetings or during times of intense research.
This is something that it took me too many years to learn.
I think the need for this quiet time is particularly true at busy meetings or during times of intense research.
Organising principles for quantum effects in condensed phases
At the workshop a couple of talks have brought home to me two important organising principles for understanding and describing quantum effects involving hydrogen bonding in condensed phases. These are relevant to a wide range of problems from properties of bulk water to proton transfer in enzymes.
1. Competing quantum effects.
In hydrogen bonding as the donor acceptor distance decreases the hydrogen bonding gets stronger. This decreases the frequency of the O-H stretch on the donor and increases the frequency of the O-H bend.
[This can be seen in Figures 5 and 6 in my CPL]. Consequently, their are two competing contributions to the zero-point energy. These reduce the total quantum effect and also make it more challenging to calculate accurately.
This idea was highlighted in a 2007 JCP by Scott Habershon, Tom Markland, and David Manolopoulos and a 2012 PNAS by Tom Markland and Bruce Berne.
On tuesday, Tom Markland highlighted how these competing quantum effects were important for understanding isotope effects in the enzyme Ketosteroid isomerase.
2. Rate processes dominated by rare quantum events
If one looks at the average bond lengths in aqueous systems one might think that the hydrogen bonds are weak. However, due to quantum and thermal fluctuations there are rare events where oxygen atoms are sufficiently close together that there are transient strong hydrogen bonds where protons can be delocalised between two oxygen atoms.
This was highlighted in a talk by Michele Ceriotti.
These ideas were first developed by Dominik Marx and Mark Tuckerman and are nicely summarised in Section 2 in this review. The key figure is below. The left and right plots correspond to a quantum and a classical simulation, respectively.
1. Competing quantum effects.
In hydrogen bonding as the donor acceptor distance decreases the hydrogen bonding gets stronger. This decreases the frequency of the O-H stretch on the donor and increases the frequency of the O-H bend.
[This can be seen in Figures 5 and 6 in my CPL]. Consequently, their are two competing contributions to the zero-point energy. These reduce the total quantum effect and also make it more challenging to calculate accurately.
This idea was highlighted in a 2007 JCP by Scott Habershon, Tom Markland, and David Manolopoulos and a 2012 PNAS by Tom Markland and Bruce Berne.
On tuesday, Tom Markland highlighted how these competing quantum effects were important for understanding isotope effects in the enzyme Ketosteroid isomerase.
2. Rate processes dominated by rare quantum events
If one looks at the average bond lengths in aqueous systems one might think that the hydrogen bonds are weak. However, due to quantum and thermal fluctuations there are rare events where oxygen atoms are sufficiently close together that there are transient strong hydrogen bonds where protons can be delocalised between two oxygen atoms.
This was highlighted in a talk by Michele Ceriotti.
These ideas were first developed by Dominik Marx and Mark Tuckerman and are nicely summarised in Section 2 in this review. The key figure is below. The left and right plots correspond to a quantum and a classical simulation, respectively.
Tuesday, July 9, 2013
Elucidating singlet fission
Singlet fission is the process where a excited spin singlet state of an organic molecular complex can decay into two spin triplet states on spatially separated molecules. This process has received considerable attention recently because of the possibility of using it to increase the efficiency of organic photovoltaic cells. Several previous posts considered some of the fascinating science involved, including the reverse process of triplet-triplet annihilation.
There are a beautiful series of papers by Timothy Berkelbach, Mark Hybertsen, and David Reichman
Microscopic theory of singlet exciton fission. I. General formulation
Microscopic theory of singlet exciton fission. II. Application to pentacene dimers and the role of super exchange
To me these papers provide a quality benchmark for theoretical work in the field and highlight the limitations and confusion of some of the previous work on the subject.
Why do I like the papers? The authors
There are a beautiful series of papers by Timothy Berkelbach, Mark Hybertsen, and David Reichman
Microscopic theory of singlet exciton fission. I. General formulation
Microscopic theory of singlet exciton fission. II. Application to pentacene dimers and the role of super exchange
To me these papers provide a quality benchmark for theoretical work in the field and highlight the limitations and confusion of some of the previous work on the subject.
Why do I like the papers? The authors
- use diabatic states as a starting point. This connects to chemical intuition about the mixed character of the excited states (see the Figure above).
- combine quantum chemistry calculations with effective Hamiltonians.
- highlight the importance of the environment in determining the excited state dynamics.
- acknowledge the limitations of quantum chemical calculations for providing accurate parameters for effective Hamiltonians and the excited states. This leads them to consider how the efficiency of singlet fission can vary significantly with the excited state energies and the extent of their charge transfer character (see the Figure below).
- show how the effect of the environment can be treated reasonably reliably in an [relatively low cost] approximation schemes [e.g., Redfield and Polaronic Quantum Master Equation=PQME].
- answer an important question. The singlet fission does occur via an "intermediate" charge transfer state, even when that state is at high energy.
Hopefully this approach will be applied to other important processes of relevance to organic photovoltaic cells, including charge separation in bulk heterojunction cells and in the Gratzel cell.
Seogjoo Jang, Timothy Berkelbach, and David Reichman have a preprint where they have applied the PQME formalism to a donor--bridge-acceptor system.
An outstanding challenge remains to understand how the coherent triplet pair decoheres into uncorrelated triplet states on the two molecules.
Monday, July 8, 2013
Hiking in Telluride
Besides the great science, a wonderful thing about Telluride meetings is the opportunity to do some hiking in the Rocky Mountains. This is my third time here and slowly I am finding some nice hikes that are directly accessible from the town.
I arrived one day early to try and get over jetlag. Yesterday I did the hike described here. It took about 5 hours at a leisurely place. I think Eric Bittner made me aware of this hike. A few of my photos are above. But, today I am a bit sore from all the downhill...
Disclaimer: this is for experienced fit hikers. Make sure you have adequate clothing, water, sun screen, food, map, ..... Also beware of altitude sickness.
Friday, July 5, 2013
Talk on quantum nuclear motion in hydrogen bonding
Next week I attending a Telluride Science Research Center workshop on Quantum effects in condensed phase systems.
Here is the current version of the slides for my talk, "Effect of quantum nuclear motion on hydrogen bonding."
The empirical potential energy curves used are based on the simple two-state model presented in this paper.
Comments welcome.
Here is the current version of the slides for my talk, "Effect of quantum nuclear motion on hydrogen bonding."
The empirical potential energy curves used are based on the simple two-state model presented in this paper.
Comments welcome.
Thursday, July 4, 2013
Who should be called a Professor?
Should members of senior management at universities hold the title Professor if they did not become a Professor via a normal academic career?
This question is examined for some specific cases in a fascinating blog post by UQ economics Professor Paul Fritjers.
This question is examined for some specific cases in a fascinating blog post by UQ economics Professor Paul Fritjers.
Wednesday, July 3, 2013
Desperately seeking quantum coherence
There is a paper in Science
Dugan Hayes, Graham B. Griffin, Gregory S. Engel
Six years ago Engel was first author of a Nature paper claiming that photosynthetic systems used quantum computing to maximise efficiency. The claims of this paper are more modest. The abstract begins:
The design principles that support persistent electronic coherence in biological light-harvesting systems are obscured by the complexity of such systems. Some electronic coherences in these systems survive for hundreds of femtoseconds at physiological temperatures, suggesting that coherent dynamics MAY play a role in photosynthetic energy transfer. Coherent effects MAY increase energy transfer efficiency relative to strictly incoherent transfer mechanisms.
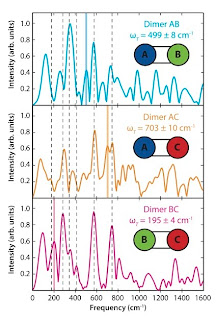
The key data is in the Figure below. It shows a Fourier transform of the "cross peaks in the two-dimensional spectra". The three boxes correspond to the different heterodimers.
The vertical dashed lines are all present in monomers and are identified as vibronic features of those monomers.
[n.b. In the past some people mistakenly identified such features with coherences between different chromophores in photosynthetic complexes.]
The solid coloured vertical lines are identified as a quantum beating coherence between the two monomors. [But note smaller versions of these peaks are also present in two of the heterodimers]. The corresponding frequencies correspond to the difference frequency epsilon between the two monomers. This is the main result of the paper, the presence of electronic coherences between two dimers.
The decoherence time of the coherences is estimated to be of the order of tens of femtoseconds.Although, not stated in the paper, this is just what one expects for typical chromophores in polar solvents. This timescale is much shorter than the timescale [1-100 psec] for many of the exciton transport processes in photosynthetic systems.
In a heterodimer the quantum beat frequency is given by
where Delta* is the coupling energy between the two chromophores and epsilon is the energy difference between the excitons in the individual chromophores. Since the authors observe a beat frequency of close to epsilon this means that Delta* is very small, at most tens of cm-1 which is less than thermal energy scales at room temperature.
It should also be pointed out that in the regime where epsilon is much larger than Delta* that the spectral weight of the quantum coherences becomes very small and they are easily decohered. This can be seen in Figure 2 of this PRL by Costi and Kieffer.
Tuesday, July 2, 2013
Are quantum effects ever enhanced in condensed phases?
Previously, I asked the question: are there any condensed phase systems in chemistry where quantum effects [e.g. tunneling, interference, entanglement] are enhanced compared to the gas phase?
Let me clarify. Suppose we take a molecular system X and consider the magnitude of some quantum effect Y in the gas phase. We then put X in some condensed phase environment [e.g., solvent, protein, or glass] and measure or calculate Y.
It is quite possible that Y increases due to what I would call "physically trivial" effects, e.g. a change in the geometry of X which makes Y larger. For example, the polarity of a solvent can decrease the donor-acceptor distance for proton transfer in a molecule and thus increase quantum tunnelling.
To me a physically "non-trivial" effect is where the environment enhances the quantum effect for the same reference system X [e.g., one uses the same geometry of the molecule in the gas and condensed phases]. I am not sure this ever happens. Generally, environments decohere quantum systems.
But I stress that such environmental effects can be far from "trivial" to chemists and biologists. e.g., they can make an enzyme work!
Historically, this distinction between "trivial" and "non-trivial" environmental effects was important and confusing for the Caldeira-Leggett model for quantum tunneling in the presence of an environment. To clarify this issue Caldeira and Leggett added a "counter-term" to the Hamiltonian to subtract off the renormalisation of the potential barrier by the environment. This is discussed in detail in the book by Weiss [page 19 in the second edition]. Chemists call this "counter-term" the solvation energy.
Aside: in nuclear physics these renormalisation effects are observable and calculable, as described in this PRL.
Let me clarify. Suppose we take a molecular system X and consider the magnitude of some quantum effect Y in the gas phase. We then put X in some condensed phase environment [e.g., solvent, protein, or glass] and measure or calculate Y.
It is quite possible that Y increases due to what I would call "physically trivial" effects, e.g. a change in the geometry of X which makes Y larger. For example, the polarity of a solvent can decrease the donor-acceptor distance for proton transfer in a molecule and thus increase quantum tunnelling.
To me a physically "non-trivial" effect is where the environment enhances the quantum effect for the same reference system X [e.g., one uses the same geometry of the molecule in the gas and condensed phases]. I am not sure this ever happens. Generally, environments decohere quantum systems.
But I stress that such environmental effects can be far from "trivial" to chemists and biologists. e.g., they can make an enzyme work!
Historically, this distinction between "trivial" and "non-trivial" environmental effects was important and confusing for the Caldeira-Leggett model for quantum tunneling in the presence of an environment. To clarify this issue Caldeira and Leggett added a "counter-term" to the Hamiltonian to subtract off the renormalisation of the potential barrier by the environment. This is discussed in detail in the book by Weiss [page 19 in the second edition]. Chemists call this "counter-term" the solvation energy.
Aside: in nuclear physics these renormalisation effects are observable and calculable, as described in this PRL.
Monday, July 1, 2013
Where is your loyalty?
There is a recent article in The Chronicle of Higher Education about what role, if any, "loyalty" should play in giving permanent jobs to faculty on "casual contracts" [referred to as adjuncts in the article]. The article and the comments highlight, at least to me, how the notion of "loyalty" is an ill-defined and highly emotionally charged concept.
Surviving and succeeding in science [and academia in general] requires building, maintaining, and preserving a complex array of personal relationships. The notion of loyalty can have a significant effect, both for good and bad, on these relationships.
The problem is that different people may have very different expectations about where loyalty should lie and what it means.
Loyalty can affect information flow, response to criticism, and the sharing of resources.
Here are some situations where loyalty may play out:
Surviving and succeeding in science [and academia in general] requires building, maintaining, and preserving a complex array of personal relationships. The notion of loyalty can have a significant effect, both for good and bad, on these relationships.
The problem is that different people may have very different expectations about where loyalty should lie and what it means.
Loyalty can affect information flow, response to criticism, and the sharing of resources.
Here are some situations where loyalty may play out:
- A student takes a postdoc with a competitor of his advisor.
- A graduate student is taking a class taught by her advisor. Some of the other students make a complaint about the teaching of the faculty member.
- A collaborator publicly criticises a paper you wrote without them.
- A new faculty member receives substantial start-up funds which are key to their success. They receive an offer from another institution.
Subscribe to:
Comments (Atom)
A forgotten physicist: Amelia Frank (1906-1937)
In honour of International Women's Day, I bring to your attention a fascinating recent piece in The Conversation , Who was Amelia Frank?...

-
This week Nobel Prizes will be announced. I have not done predictions since 2020 . This is a fun exercise. It is also good to reflect on w...
-
Is it something to do with breakdown of the Born-Oppenheimer approximation? In molecular spectroscopy you occasionally hear this term thro...
-
Nitrogen fluoride (NF) seems like a very simple molecule and you would think it would very well understood, particularly as it is small enou...