D*A -> D+A- (1)
One wants this to proceed much faster than than radiative or non-radiative decay of D, i.e.:
D*A -> DA + photon or heat (2)
or charge recombination
D+A- -> DA
In terms of a qualitative understanding in terms of molecular orbitals the picture below may be helpful.
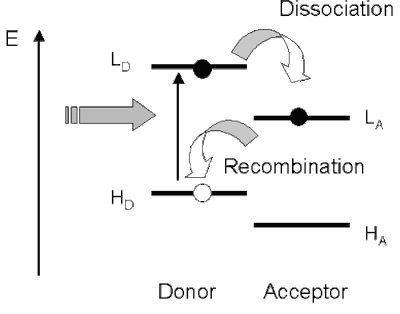
However, to be quantitative one should think in terms of the full quantum many-body states which I have denoted above DA, D*A, and D+A-.
The rate of charge separation in (1) can be described by Hush-Marcus electron transfer the
 ory.
ory.
This rate will be largest when the optical excitation energy equals the sum of the donor ionistation energy and the acceptor electron afinity plus the reorganisation energy (of the environment) associated with the charge separation.
[see the figures above to see how the electron tranfer rate drops significantly with detuning]
I believe this is may be an important design principle which I have never seen clearly stated in the literature; most people try to line up the (non-existent) LUMO energies of D and A.
A good solar cell has (1) much faster than (2).
Exactly the same physics is relevant for organic molecules used to detect trace amounts of explosives (i.e., nitroaromatics) by flourescent quenching. D the sensor should be a flourescent molecule which will bind to the nitroaromatic A strongly enough so that (1) proceeds much faster than (2), i.e, the flourescence is quenched.
A key challenge is to find donor molecules D which are only sensitive to specific nitroaromatics A. This has recently been done in a paper, that we will discuss at tomorrow's thursday COPE meeting.




It is of general consensus that the donor/acceptor LUMO level offset should be at least that of the exciton binding energy of donor. But in accordance with Marcus-Hush theory we should be aiming for an offset equal to the sum of the exciton binding energy and the charge separation reorganisation energy.
ReplyDeletefor a clearer statement of this design principle see
"Optimum energy levels and offsets for organic donor/acceptor binary photovoltaic materials and solar cells"
Sun, S.-S.
Materials Science and Engineering B, 2005, 116, 251 - 256
I'm not sure about your picture for explosives sensing, it is somewhat different from what I thought. Is there really electron transfer between the nitroaromatic and the sensor?
ReplyDeleteWouldn't it be:
The sensor molecule [DA] has some rates for (1) and (2).
When the nitroaromatic compound to be sensed is present (2) is enhanced / (1) is reduced and hence the flourescence is quenched.
The optimum is to maximise (1)/(2)[DA] while minimising (1)/(2)[DA+nitroaromatic].
Carrying on from July 12 (I'm going backwards, as you can probably tell)...
ReplyDeleteThe ensembles representing the minima of the separate 'parabolae' may not be orthogonal* if this is not mandated by the constraints. However, if they are, then this will kill the probability of of fast electron transfer, as there is no component of the first ensemble on the second.
There are well-known metrics of the space of density matrices, and if the matrices are pure, then one could equivalently speak of a generalized 'angle'. It seems likely that the reaction coordinate should depend monotonically on this angle (the constraints suggested in the July 12 post suggests one invoke an energy operator for which both of the D and A states are eigenfunctions - thereby defining a space in which both states are pure).
* Note that I am saying 'ensemble' in the sense of an ensemble of density matrices, so orthogonality should be defined as Tr(pp')=0.
There is a empirical model, called scharber's model, taking account of this offset. see "Design Rules for Donors in Bulk-Heterojunction Solar Cells—Towards 10 % Energy-Conversion Efficiency"
ReplyDelete