Kinky many-body physics

A key and profound property of quantum-many body systems is the emergence of new low energy scales that are much less than the underlying bare interactions. Classic cases are the Kondo temperature and the superconducting transition temperature in BCS theory. How the relevant low energy scales emerge in strongly correlated electron systems is an outstanding problem.

There is a very nice PRL
Poor Man’s Understanding of Kinks Originating from Strong Electronic Correlations
K. Held, R. Peters, and A. Toschi

A decade ago there was a Nature paper [where else?!] that made a big deal about the fact that they saw a kink in the quasi-particle dispersion [energy versus momentum] of a cuprate material measured by ARPES and claimed this was due to electron-phonon coupling. Hence, (!) electron-phonon coupling must be important in the cuprates. I found this claim troubling because it seemed to be based on the classic fallacy of not distinguishing sufficient and necessary conditions. Just because electron-phonon coupling can produce a kink does not mean that this is the case here. What about alternative explanations? Subsequent theoretical work, showed that electronic correlations [as captured by Dynamical Mean Field Theory (DMFT)] could also produce a kink too. This was hardly surprising to me.

The really interesting and important question is how the low energy scale [~50 meV for the cuprates] associated with the kink emerges. The authors of this PRL show that this energy scale is associated with the crossover to the strong coupling fixed point of the Kondo problem associated with the DMFT treatment of the Hubbard model.
They "emphasize that this is a radically new insight." 
I agree.

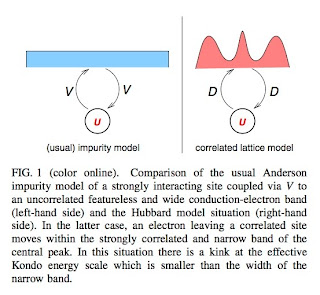
The figure below highlights the difference between the usual Anderson impurity model and the self-consistent Anderson impurity problem associated with DMFT. In the former one has the hybridisation V much less than the conduction band width W which is much less than U. In contrast for the Hubbard DMFT case the hybridisation is replaced by the bare bandwidth D [or the hopping t] which is actually larger than the (renormalised) bandwidth Gamma associated with the central peak in the spectral density.

This different hierarchy of energy scales leads to a new energy scale omega* given by

This expression is derived using a "poor man's" scaling analysis.

The figure below shows the frequency dependency of the  real part of the self energy.
At low frequencies it is linear for omega less than omega*, as expected for a Fermi liquid. The slope gives the quasi-particle renormalisation Z.

For higher frequencies it is also approximately linear for frequencies on the scale of the central peak (CP) defining a higher frequency quasi-particle weight.

A few things I would like to know in the future include how these results connect to other work.

1. The details of how this physics affects the temperature dependence of properties. A few qualitative comments are made about temperature dependence in the conclusion.

2. A recent DMFT paper found robust quasi-particles out to much higher temperatures than expected. Is this the same physics?

3. A phenomenological model self energy for the cuprates [described in a PRB by Jure Kokalj, Nigel Hussey, and I] involves crossovers at some low energy scales whose microscopic origin needs to be elucidated.

Aside: On his blog, Doug Natelson had some negative comments about PRL stimulated by the poor abstract and lack of editing (not science) of this paper.