At what temperature are quasi-particles destroyed?

An interesting question [which has featured in many of my blog posts] concerns defining the coherence temperature at which quasi-particles in a Fermi liquid are "destroyed". There are several possible experimental signatures of this:

• absence of a sharp dispersing peak in the one electron spectral density (as seen in ARPES)
• collapse of the Drude peak in the optical conductivity
• collapse of the linear in T term in the specific heat capacity
• a peak in the thermopower versus temperature
• deviations of the resistivity temperature dependence from T^2
• the resistivity becoming larger than the Mott-Ioffe-Regel limit.

I tended to think that these would all occur at the approximately the same temperature.
(A Nature paper also makes a similar assumption.)
However, Jure Kokalj pointed out to me that DMFT gives quite different temperatures for the different signatures above. For example, in this PRB the thermopower and specific heat have a peak at a temperature at which there is still a Drude peak.

A PRL I recently blogged about contains the "throw away" line that got my attention:

the Fermi liquid behavior in two-particle properties is more fragile than in single-particle ones. Indeed, in the well-known Kondo problem the Kondo resonance persists at temperatures up to 2T_K while the magnetic susceptibility saturates to a Pauli form only below T=0.2T_K.

That is an order of magnitude difference in temperature scales!

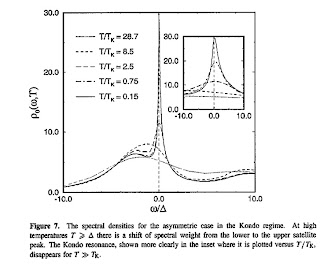
This point can be seen in this nice paper by Costi, Hewson, and Zlatic. For example, compare Figures 2, 7, and 16, which show the specific heat, spectral density, and thermopower, respectively.

It would be nice to have a simple physical picture of the origin of these disparate temperature scales. Perhaps it is something as mundane as different convolutions and moments of the Fermi-Dirac distribution.