Simplifying the Theory of Everything

This weeks reading from Advanced Solid State Physics by Philip Phillips is Chapter 2, The Born-Oppenheimer [BO] Approximation.

This reflects a key idea in quantum many-body theory: when there is a clear separation of energy scales one can often simplify the theory greatly and identify distinct quasi-particles [e.g., phonons and electronic quasi-particles] corresponding to the different energy scales.

Without BO there would be no quantum chemistry and no quantum theory of electronic properties of crystals.

BO is a consequence of the fact that electrons are much lighter than nuclei. Consequently, electrons in a molecule or solid have average velocities that are typically orders of magnitude faster than the nuclei.

Equation (2.1) is the Hamiltonian

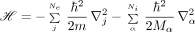
The symbols Zα and Mα are the atomic number and mass of the α^th nucleus, Rα is the location of this nucleus, e and m are the electron charge and mass, r _j is the location of the j ^th electron, and ℏ is Planck's constant.

If we could solve this Hamiltonian we would have Laughlin and Pines Theory of Everything.

Equations (2.10) and (2.14) are the key results of the chapter.

But there are many interesting and important situations where BO breaks down. Cases for molecules are discussed here.