The focus is on spin liquids: how to define them and whether they exist in real materials and/or whether they are the ground state of physically reasonable quantum lattice Hamiltonians.
Bruce considers three different classes of spin liquids, each being defined by their excitation spectrum. In the figure below, singlets are red and triplets are blue.
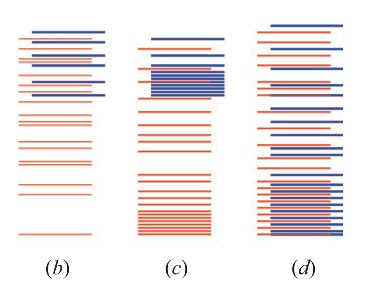
(b) Type I. There is gap between the singlet ground state and both the lowest-lying triplet state and the first excited singlet state.
(c) Type II. There is gap between the singlet ground state and the lowest-lying triplet state. There is no gap to a continuum of low-lying singlet states.
(d) Algebraic spin liquids. There is no gap to either the lowest-lying triplet state or the first excited singlet state.
An important question is how to distinguish these different states experimentally. One basic question I am not clear on is: what are the qualitative differences between the dynamical spin susceptibility for the three different classes of spin liquids? This susceptibility is the quantity which determines inelastic neutron scattering cross sections and the NMR relaxation rate.
I believe singlet excitations do not contribute to the susceptibility but cannot find a proof of this. [Maybe work in the spectral representation and show that the relevant matrix elements between the singlet ground state and a singlet excited state must be zero?]
All these excitations will contribute to the specific heat capacity at low temperatures and the thermal conductivity. The singlet spectrum will not shift in a magnetic field but the triplets will split and the corresponding spectral weight be redistributed.
An what does this have to do with superconductivity? Well,.. strong coupling RVB-type theories focus on singlet excitations whereas weak-coupling AFM fluctuation theories focus on triplet excitations. This important point is nicely emphasized and discussed in this review on the cuprates by Mike Norman.




No comments:
Post a Comment