What is a metal?
How does one distinguish a metal from an insulator? One signature might be the presence of a charge gap at the chemical potential.
Is there a broken symmetry associated with a metal-insulator phase transition?
A key concept emphasized by Anderson is that distinct phases of matter are associated with the rigidity of their order parameter. For example, for a superconductor the superfluid density is associated with the phase stiffness of the ground state wave function.
It turns out that the Drude weight and the charge compressibility are both zero in a Mott insulator and non-zero in a metal. This is discussed in an interesting article by Imada.
Aside: Imada's paper assumes the metal-insulator transition is continuous (i.e. not first-order) and derives scaling relations for the transition. This assumption may not be valid. At least, in dynamical mean-field theory the Mott transition at half filling is first order.
Kohn (and later Thouless) emphasized that for a metal one could calculate the Drude weight from the size and twist dependence of the ground state energy in the presence of twisted boundary conditions.
Imada considered a system at finite temperature and considered twisted boundary conditions in the imaginary time direction [anti-periodicity for fermions is required by the Kubo-Martin-Schwinger condition] showed that the charge compressibility determines the twist dependence.
I would be interested to see how the Drude weight and charge compressibility vary as one increases the temperature through the Fermi liquid - bad metal crossover.
Is there a broken symmetry associated with a metal-insulator phase transition?
A key concept emphasized by Anderson is that distinct phases of matter are associated with the rigidity of their order parameter. For example, for a superconductor the superfluid density is associated with the phase stiffness of the ground state wave function.
It turns out that the Drude weight and the charge compressibility are both zero in a Mott insulator and non-zero in a metal. This is discussed in an interesting article by Imada.
Aside: Imada's paper assumes the metal-insulator transition is continuous (i.e. not first-order) and derives scaling relations for the transition. This assumption may not be valid. At least, in dynamical mean-field theory the Mott transition at half filling is first order.
Kohn (and later Thouless) emphasized that for a metal one could calculate the Drude weight from the size and twist dependence of the ground state energy in the presence of twisted boundary conditions.
Imada considered a system at finite temperature and considered twisted boundary conditions in the imaginary time direction [anti-periodicity for fermions is required by the Kubo-Martin-Schwinger condition] showed that the charge compressibility determines the twist dependence.
I would be interested to see how the Drude weight and charge compressibility vary as one increases the temperature through the Fermi liquid - bad metal crossover.
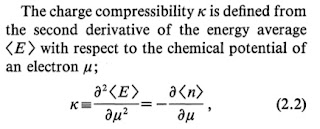




You could also ask the question - When is a metal?
ReplyDeleteSorry, the software borks the link.
ReplyDeletehttp://rsta.royalsocietypublishing.org/content/368/1914/941.full.pdf
But what about Anderson insulators? e.g. insulators via disorder without long-range Coulomb interaction. They presumably have finite compressibility.
ReplyDelete