Emergence of dynamical particle-hole asymmetry II

This follows an earlier post Emergence of dynamical particle-hole asymmetry concerning the new approach of Sriram Shastry to doped Mott insulators, describing them as an extremely correlated Fermi liquid, and characterised by two self energies.

There is a nice preprint
Extremely correlated Fermi liquid theory meets Dynamical mean-field theory: Analytical insights into the doping-driven Mott transition
Rok Zitko, D. Hansen, Edward Perepelitsky, Jerne Mravlje, Antoine Georges, Sriram Shastry

The part ice-hole asymmetry means that electron-like quasi-particles have much longer lifetimes than hole-like quasi-particles. This means that the imaginary part of the (single-particle Dyson) self energy Sigma(omega) is asymmetric about omega=0, the chemical potential.

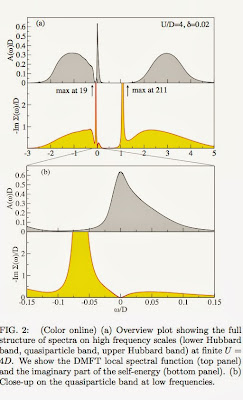
Here are two particularly note-worthy figures from the paper.
The first shows how the asymmetry at omega=0 is associated with the quasi-particle band (QPB) at the top of the lower Hubbard band (LHB). This band emerges as the Mott insulator is doped. The suppression of the density of states A(omega) between the QPB and LHB, means that Im Sigma(omega) must be very large in that energy/frequency range (omega ~ -0.01). A similar requirement does not hold for positive omega, leading to the large electron-hole asymmetry.

The figure below shows a fit of the frequency dependence of the imaginary part of the self energy, calculated using Dynamical Mean-Field Theory (DMFT), to a form given by the Extremely Correlated Fermi Liquid (ECFL) theory.

Note the large particle-hole asymmetry and how it increases with decreasing doping. A regular Fermi liquid would simply have an inverted parabola with a maximum at omega=0.

I thank Rok, Jerne, and Sriram for helpful discussions about their work.